4.8.1 Одновременное изменение направления на объект маневра и дистанции до него
Одновременное изменение направления на объект маневра и дистанции до него является наиболее общей задачей тактического маневрирования. Большинство других задач на изменение позиции сводится к частным случаям этой общей задачи.
Чтобы рассчитать маневр, необходимо знать элементы движения объекта маневра Кк и Vк а также элементы позиции маневрирующего корабля П0, D0 на момент начала выполнения маневра. Предположим, что в заданный момент времени T0 маневрирующий корабль находится относительно объекта маневра по пеленгу П0 в дистанции D0 (рис. 4.8). Объект маневра следует курсом Кк и скоростью Vк.
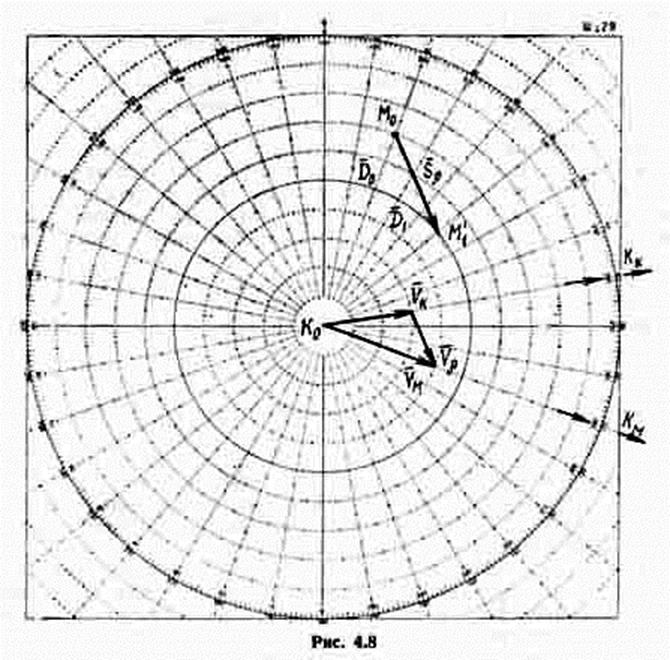
Для выполнения поставленной задачи маневрирующему кораблю необходимо изменить и направление, и дистанцию, то есть занять новую позицию М '1 по пеленгу П1 и на дистанции D1 . В общем случае данная задача имеет множество решений, но чаще всего производится расчет курса для изменения позиции при назначенной скорости хода. Эта скорость назначается исходя из возможностей энергетической установки, поставленной задачи, гидрологических условий.
Решение задачи начинается с построения треугольника позиций. Считая, что объект маневра К находится в центре планшета, по пеленгу П0 и на дистанции D0 от него наносят начальную позицию М0 маневрирующего корабля, по заданным П1 и D1 - относительную позицию M '1. Вектор М0М '1 является вектором относительного перемещения Sr. Для определения курса маневрирующего корабля строится треугольник скоростей. Из центра планшета K0 откладывается вектор Vк, а из его конца параллельно вектору Sr и в том же направлении проводится линия относительного курса Kr до пересечения с окружностью планшета, соответствующей заданной скорости маневрирующего корабля Vм. В точке пересечения сходятся концы векторов Vм (начало в центре планшета) и Vr (начало в конце вектора Vк). направление вектора Vм, снятое с внешней шкалы маневренного планшета, дает искомый курс маневрирующего корабля Км для изменения позиции. Если при построении треугольника скоростей линия относительного курса пересекает окружность, соответствующую Vм в двух точках, то это значит, что маневр заданной скоростью выполним двумя курсами. Из двух решений выбирается то, которое удовлетворяет требованиям поставленной задачи.
Чтобы найти время маневра, нужно, исходя из масштабов построений, определить величину относительного перемещения Sr, величину относительной скорости Vr и рассчитать время маневра t = Sr /Vr.
4.8.2 Изменение дистанции при постоянстве пеленга
Маневр изменения дистанции применяется в том случае, когда направление на объект маневра уже удовлетворяет поставленной задаче. Эта задача решается как частный случай рассмотренной выше задачи изменения позиции.
При построении треугольника позиций относительная позиция М '1 (рис. 4.9) будет находиться на линии начального пеленга на заданной дистанции D3 от объекта маневра, то есть линия относительного перемещения совпадает с линией начального пеленга. Поэтому треугольник позиций представляет собой прямую линию К0М0М '1.
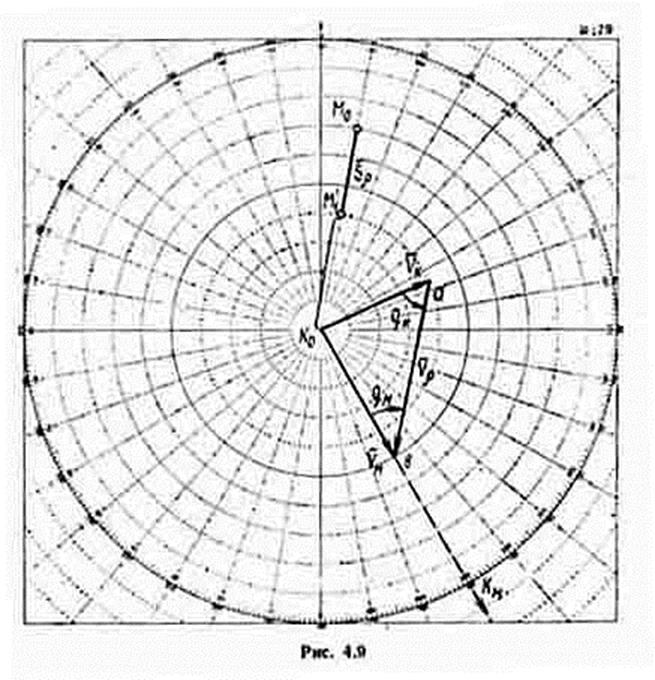
Решение скоростного треугольника для определения курса маневрирующего корабля при заданной скорости осуществляется так же, как и при решении задачи на изменение позиции (см. рис. 4.8). Время выполнения маневра определяется отношением t = (D0 - D3) / Vr.
Из треугольника скоростей следует, что
Vм sin qм = Vк sin qк. (4.24)
Поэтому
sin qм = (Vк / Vм) sin qк. (4.25)
Если при постоянстве пеленга происходит сближение кораблей, то правая и левая части (4.24) будут иметь противоположные знаки (корабли маневрируют разноименными бортами). Тогда ОБП = БПм + БПк = 0, то есть, сближаясь при постоянстве пеленга, корабли М и К придут в точку пересечения линий их курсов одновременно. В связи с этим, обнаружив, что пеленг на приближающийся корабль не меняется, во избежание столкновения необходимо нарушить равенство боковых перемещений изменением курса или скорости своего корабля.
Рассмотренный маневр изменения дистанции без изменения пеленга позволяет сделать следующие выводы:
- маневр изменения дистанции при постоянстве пеленга можно выполнить относительно объекта, курс и скорость которого неизвестны, для этого необходимо добиться равенства боковых перемещений;
- из выражения (4.25) вытекает возможность определения одного из элементов движения цели, когда известен другой:
qк = arcsin [(Vм / Vк) sin qм];
Vк = Vм sin qм / sin qк.
Наиболее часто этот маневр применяется при выходе в атаку, особенно на малых дистанциях, когда необходимо сократить дистанцию и уточнить элементы движения цели, сохранив ее курсовой угол.
4.8.3 Изменение дистанции до цели курсом, равным или обратным начальному пеленгу на нее
При обнаружении цели на больших дистанциях, когда величина изменения пеленга мала, а элементы движения цели определить не представляется возможным, целесообразно применение маневра курсом, равным пеленгу обнаружения, для сокращения дистанции, или курсом, обратным пеленгу, для ее увеличения. Обоснование этого способа изменения дистанции вытекает из формулы (4.23). Действительно, независимо от элементов движения цели маневрирование на своем курсовом угле 0 или 180° ведет к максимальной скорости изменения расстояния между кораблями, так как второй член равенства (4.23) при qr = 0° (180°) приобретает максимальное значение.
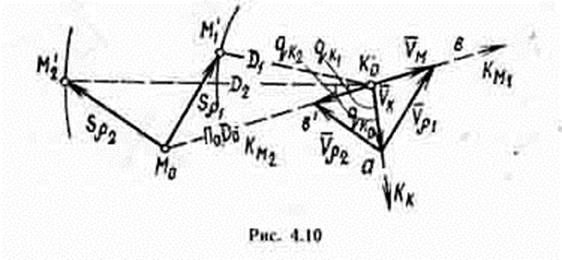
В процессе выполнения данного маневра всегда будет происходить увеличение курсового угла цели независимо от того, какая решается задача - сближение или расхождение с целью. Это наглядно представлено на рис. 4.10, где показан характер относительного перемещения корабля при сокращении и при увеличении дистанции. Если корабль для сокращения дистанции ляжет на курс Км1, равный начальному пеленгу на цель, то в соответствии с треугольником скоростей К0аb сближение на заданную дистанцию произойдет в позиции М '1 на курсовом угле цели qк1 > qк0. Если тому же кораблю необходимо оторваться от цели, то курсом Км2 (треугольник скоростей К0аb') он выйдет на заданную дистанцию D2 в позиции М '2 на курсовой угол цели qк2 > qк0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.