Угол qр между вектором П0D0 и вектором Sr называется относительным курсовым углом.
Угол М '1К0М0 есть приращение пеленга за время маневра. Он равен разности пеленгов П1 - П0 и обозначается буквой q.
Треугольник позиций дает геометрическую картину маневра в относительном движении, т. е. показывает перемещение маневрирующего корабля относительно объекта маневра.
Треугольник М0М1М '1, сторонами которого являются векторы перемещения маневрирующих кораблей Sм, Sк, Sr, называется треугольником перемещений. Он служит для перехода от относительного движения к абсолютному и показывает взаимосвязь абсолютных перемещений Sм и Sк маневрирующих кораблей и относительного перемещения Sr. Треугольник перемещений строится при начальной позиции маневрирующего корабля приемом обратного построения, то есть решается уравнение Sr = Sм - Sк.
Для определения абсолютной позиции маневрирующего корабля в конце маневра, то есть для перехода от относительного движения к абсолютному, необходимо из начальной позиции маневрирующего корабля М0 провести линию его курса Kм, а из относительной позиции М '1 - линию курса объекта маневра Кк. В точке пересечения линий этих курсов н будет позиция маневрирующего корабля к моменту окончания маневра (точка М1).
Если построить треугольник перемещений за время маневрирования, равное единице, получим треугольник М0аb со сторонами VM, VK, Vr, который называется треугольником скоростей.
Треугольник скоростей определяет взаимосвязь курсов кораблей К и М с курсом и скоростью относительного движения.
Существуют два приема построения треугольников скоростей: прямой и обратный.
При прямом построении векторы Vм и Vк прокладываются из одной точки, а вектор относительной скорости Vr соединяет конец вектора Vк с концом вектора Vм, то есть при таком построении графически решается уравнение Vм = Vк + Vr. Таким приемом построен треугольник К0а' b'.
Обратное построение отличается от прямого тем, что концы векторов Vм и Vк сходятся в одной точке, а вектор относительной скорости Vr соединяет начала обоих векторов, то есть решается уравнение Vr = Vм - -Vк. Таким приемом построен треугольник М0аb.
Способ построения треугольника скоростей зависит от известных в условии задачи элементов, составляющих треугольник.
Треугольники скоростей, перемещений н позиций связаны между собой:
- треугольник перемещений и треугольник позиций имеют общую сторону Sr;
- треугольник скоростей и треугольник перемещений подобны, поэтому Sм / Vм = Sк / Vк = Sr / Vr = t. Значит, время маневра можно найти через элементы абсолютного, переносного и относительного движения;
- общим элементом для всех трех треугольников маневрирования является относительный курс Кr.
Одновременное рассмотрение треугольников маневрирования дает возможность наглядно представить весь маневр как в относительном, так и в абсолютном движении.
Кроме точного решения задач маневрирования с помощью векторных треугольников используется метод с применением основных элементов маневрирования - величин, характеризующих скорость изменения пеленга и дистанции.
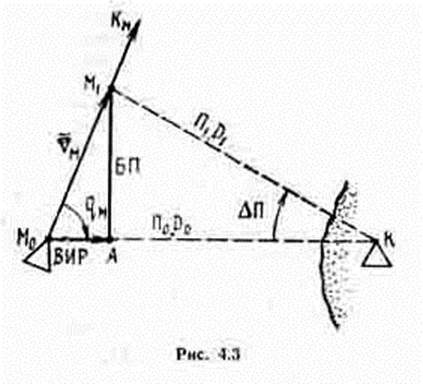
Пусть корабль маневрирует из начальной позиции М0 (рис. 4.3) постоянными курсом и скорость относительно объекта К. Скорость изменения дистанции и пеленга можно определить как первые производные этих величин по времени:
VD = dD / dt; (4.5)
wп = dП / dt, (4.6)
Из выражений (4.5) и (4.6) можно определить элементарные приращения дистанции и пеленга:
dD = VDdt; (4.7)
dП = wпdt. (4.8)
Разложив вектор скорости корабля Vм на составляющие, направленные по линии начального пеленга и перпендикулярно к нему, получим мгновенные скорости изменения расстояния VD и пеленга wп:
VD = - Vм cos qм. (4.9)
Знак VD определяется величиной курсового угла. При курсовых углах от 0 до 90° VD имеет отрицательный знак (дистанция уменьшается), при курсовых углах от 90 до 180° - положительный (дистанция увеличивается).
Угловая скорость изменения пеленга определяется поперечной составляющей вектора скорости Vм и расстоянием D между маневрирующим кораблем и объектом маневра:
VБП = D dП / dt. (4.10)
Поперечная составляющая называется мгновенной скоростью бокового перемещения корабля. Из рис. 4.3 следует, что
VБП = Vм sin qм. (4.11)
Тогда, учитывая (4.10), получим
wп = dП / dt = VБП / D = Vм sin qм / D. (4.12)
Знаки wп и VБП совпадают. Они определяются знаком приращения пеленга при его изменении. При маневрировании относительно объекта маневра правым бортом приращение пеленга положительно, левым - отрицательно.
Значения первых производных дистанции и пеленга по времени называют величиной изменения расстояния (ВИР) и величиной изменения пеленга (ВИП), а вспомогательную величину VБП - боковым перемещением (БП).
Итак, если величины ВИР и БП выражаются в тех же единицах, что и скорости кораблей, то для их вычисления пользуются формулами:
ВИРм = - Vм cos qм ; (4.13)
БПм = Vм sin qм . (4.14)
Выражая ВИП в градусах в минуту, можно записать:
ВИП = 57,3 БП / D. (4.15)
Величины ВИР и БП выражаются в кабельтовых в минуту, ВИП - в градусах в минуту. Если же в формулах (4.13) и (4.14) скорость хода берется в узлах, эти формулы примут вид:
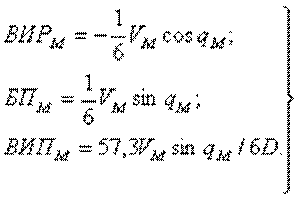(4.16)
В формулах (4.9) - (4.12) курсовой угол qм и мгновенные скорости изменения дистанции, бокового перемещения и пеленга непрерывно изменяются. Поэтому для отыскания по ним точных значений изменения пеленга и дистанции, необходимо было бы интегрировать правые части выражений (4.7) и (4.8) по дистанции и курсовому углу (пеленгу), а левые - по времени:
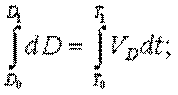
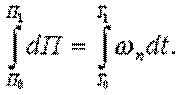
Тогда
D1 - D0 = VDt; (4.17)
П1- П0 = wпt. (4.18)
В практике тактического маневрирования элементы позиций D1, П1 по истечении времени вычисляют по формулам, вытекающим из (4.17) и (4.18):
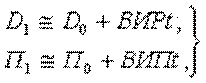(4.19)
где t - время маневра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.