МКЭ-процессор. Главное окно МКЭ процессора. Подзадачи. Структура данных МКЭ. Решатели. Конечные элементы, страница 14

Для легкого заполнителя пренебрегаем пуассоновскими эффектами по нормали и напряжениями, действующими в окружном и продольном направлении. Тогда в энергии деформации учитывается только работа нормальных напряжений на деформациях растяжения-сжатия нормали и напряжений поперечного сдвига на соответствующих деформациях.

Геометрические параметры: 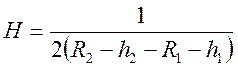 - полутолщина заполнителя; l - полудлина элемента вдоль образующей;  - полуугол.

Перемещения на поверхности раздела на расстоянии h (со знаком) от координатной поверхности найдем из (18):

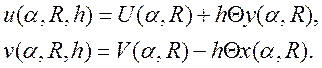                                                                 (30)

Деформация сжатия нормали:

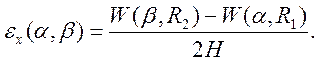                                                                 (31)

Деформация поперечного сдвига в точке (в среднем по толщине):

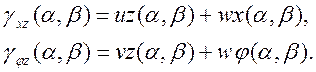                                                                 (32)

Тогда энергия деформации

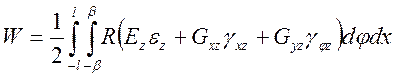                                                    (33)

и матрица жесткости для легкого заполнителя будет иметь вид:

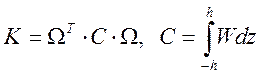                                                          ,               (34)

где  - матрица перехода от базисных функций к перемещениям (размером 40х40).

Матрица геометрической жесткости.

Для вычисления матрицы геометрической жесткости элемента шпангоута статическое деформирование рассматривается в следующих предположениях:

1. доминирующими являются окружные напряжения;

2. обжатие нормали достаточно мало.

Нелинейные составляющие окружных деформаций определяются производными по дуговой координате от перемещений в нормальном, осевом и окружном направлениях.

Работа докритических напряжений на нелинейных составляющих деформаций (с точностью до постоянного множителя) определяется выражениями:

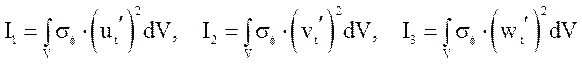                           ,                                                                             (35)

где  - оператор дифференцирования по дуговой координате:

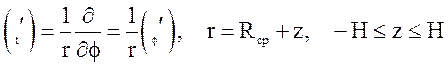                                           .                                                                             (36)

Реализация.

Элемент реализован в виде класса StiffBakulZapShell (модуль UShellBakulZap). В классе перекрыты процедуры формирования матрицы жесткости int Calculation(), вычисления результатов int ResCalculation(), формирования геометрической матрицы жесткости int UCalculation(TFEResultTab*). 

            Для промежуточных вычислений определены дополнительные классы:

class ElastBakulZapShell: public ElastLaminShell – матрица упругости для восьмиузлового элемента (легкого заполнителя);

class UStressZap – используется при вычислении матрицы геометрической жесткости;

class C_Int_ZapElem – «интеграл в коэффициентах» для заполнителя цилиндрического элемента;

class Inv_CA_ZapElem – обратная матрица перехода для заполнителя цилиндрического элемента (для перехода от неопределенных коэффициентов к узловым неизвестным, размер 40 строк  на 40 столбцов);

class LocalBakZap – матрица перехода для заполнителя цилиндрического элемента;

class DefCoefBakZap – матрица деформаций в коэффициентах для заполнителя цилиндрического элемента (размер 6 на 40);

class MatrDefBakZapPrepared – матрица деформаций не умноженная на матрицу определенную классом DefCoefBakZap (размер 40 на 1);

class MatrDefBakZap – матрица деформаций;

class MatrNBakZap – матрица напряжений;

Помимо процедур, унаследованных от базового класса, введены вспомогательные процедуры:

Вспомогательные процедуры
Название	Комментарий
int FormCInt(C_Int_ZapElem *IntC);	- формирование «интеграла в коэффициентах»
int FormCDef(DefCoefBakZap *DefC);	- формирование матрицы деформаций в коэффициентах для заполнителя
int FormCUInt(C_Int_ZapElem *IntC);	(?)

9.7 Трехслойный цилиндрический КЭ (жесткий заполнитель)

Матрица жесткости для жесткого заполнителя.

Перемещения в точке :

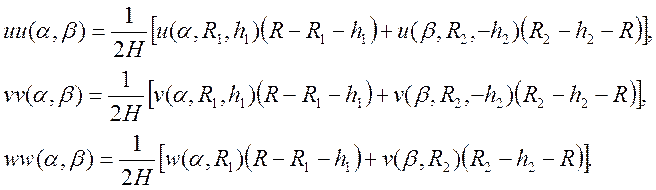                                                                                            (37)

Деформация в точке :

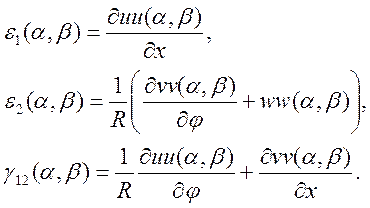                                                         (38)

Тогда энергия деформации

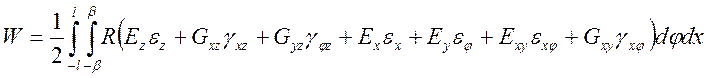                                                                                    (39)

и матрица жесткости имеет вид:

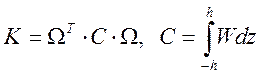                                                          .               (40)

Реализация.

Элемент реализован как производный от StiffBakulZapShell класс StiffBakulHardZapShell (модуль UShellBakulZap). В классе перекрыты унаследованные от класса StiffBakulZapShell процедуры int FormCInt(C_Int_ZapElem *IntC), int FormCDef(DefCoefBakZap *DefC), int FormCUInt(C_Int_ZapElem *IntC).

9.8 Четырехугольная пластина

Реализация.

Элемент реализован как производный от StiffElem класс StiffLaminShell4 (модуль UShellLamin4). В классе перекрыты процедуры формирования матрицы жесткости int Calculation(), вычисления результатов int ResCalculation(), формирования геометрической матрицы жесткости int UCalculation(TFEResultTab*).

Для промежуточных вычислений введены вспомогательные процедуры:

Вспомогательные процедуры
Название	Коментарий
double FMatr(TNodeCoord* xyz)	формирует матрицу перехода от неопределенных коэффициентов к узловым неизвестным (вычисляется аналитически, на основе заранее рассчитанной символьной матрицы)
double IntegrBTDB(TNodeCoord* xyz)	проинтегрированная матрица BTDB (вычисляется аналитически, на основе заранее рассчитанной символьной матрицы)
double IntegrGeomBTDB(TNodeCoord* xyz,TFEResultTab*)	проинтегрированная матрица геометрической жесткости (вычисляется аналитически, на основе заранее рассчитанной символьной матрицы)