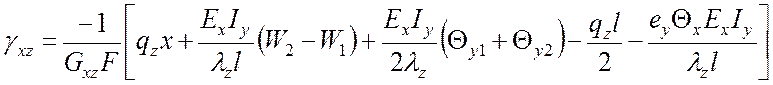МКЭ-процессор. Главное окно МКЭ процессора. Подзадачи. Структура данных МКЭ. Решатели. Конечные элементы, страница 12

.                                                                             (9)

Деформации изменения кривизны оси балки будут следующими:

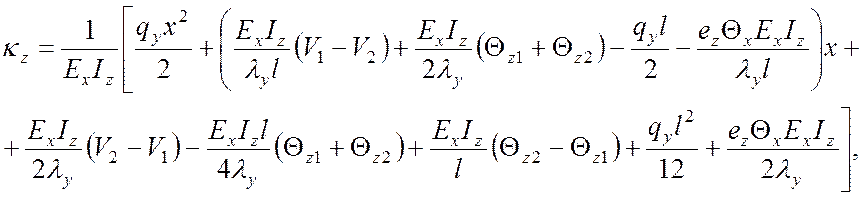                                                                             (10)

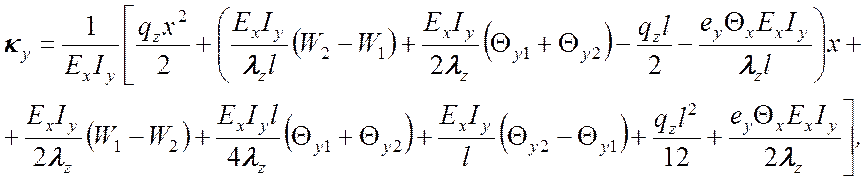                                                                             (11)

где

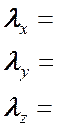                                                                            ,                                (12)

 и  - жесткости на сдвиг и изгиб соответственно.

            Полная энергия деформации может быть найдена интегрированием по длине работы интегральных сил и моментов в сечении на одноименных деформациях:

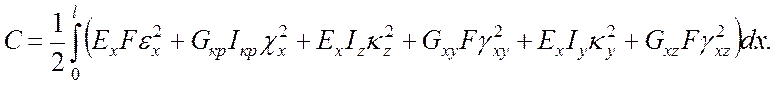                                                                             (13)

Тогда матрица жесткости может быть найдена следующим образом:

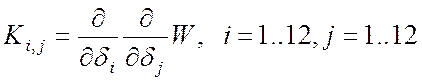                                             ,  (14)

где .

Матрица геометрической жесткости    

Для вычисления матрицы геометрической жесткости элемента статическое деформирование рассматривается в предположении, что доминирующими являются осевые напряжения. Нелинейная составляющая продольной деформации определяется следующим образом:

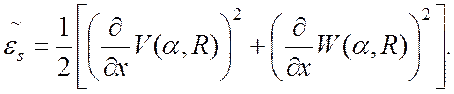                                                                                                                        (15)

Нелинейная добавка энергии деформации выражается через узловые неизвестные в виде квадратичной формы:

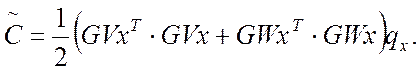                                                (16)

Тогда матрица геометрической жесткости найдется интегрированием (16) по длине элемента:

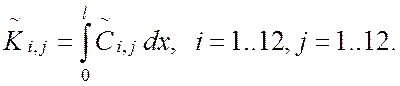                                                   (17)

Реализация.

Элемент реализован в классе StiffBeamShell (модуль UShellBeam), перекрыты процедуры формирования матрицы жесткости int Calculation() и вычисления результатов int ResCalculation().

Для формирования матрицы геометрической жесткости описан отдельный класс StiffBeamShellU (модуль UShellBeamU), производный от класса StiffBeamShell. В нем перекрыта виртуальная процедура формирования матрицы геометрической жесткости int UCalculation(TFEResultTab*).

            Вычисление матриц жесткости и геометрической жесткости производится аналитически с использованием предварительно рассчитанных в символьном виде матриц.

9.5 Цилиндрический КЭ Бакулина

            Круговая цилиндрическая моментная ортотропная оболочка. Внешняя нагрузка на оболочку может быть задана в виде нормального давления и (или) погонной силы на кромке. Для моделирования используется прямоугольный цилиндрический конечный элемент, позволяющий точно задать форму цилиндрической оболочки (рис. 3). Жесткостные характеристики могут меняться от элемента к элементу, что позволяет рассчитывать оболочки с переменной жесткостью в окружном и меридиональном направлениях. Интенсивность распределенной нагрузки может быть различной для элементов оболочки.

Рисунок 3. Цилиндрический прямоугольный элемент

Обозначения:

R – радиус срединной поверхности;

h – полутолщина;

β – полуугол конечного элемента;

l – полудлина элемента;

1,2,3,4 – номера узлов конечного элемента;

s,t,n – оси местной системы координат элемента;

- деформации срединной поверхности в осевом и окружном направлениях;

- деформация сдвига срединной поверхности;

- деформации изменения кривизны срединной поверхности;

- деформация кручения срединной поверхности;

- осевые, касательные (по окружности) и радиальные (по нормали) перемещения;

- линейные координаты в осевом и окружном направлении;

- угловая координата в окружном направлении.

Гипотезы деформирования: за основу принимается гипотеза прямой нормали, согласно которой прямолинейный элемент несущего слоя, нормальный к его срединной поверхности, после деформации остается прямолинейным, перпендикулярным к деформированной срединной поверхности несущего слоя, сохраняя при этом свою длину.

Связь коэффициентов при базисных функциях с перемещениями координатной поверхности принимается в виде:

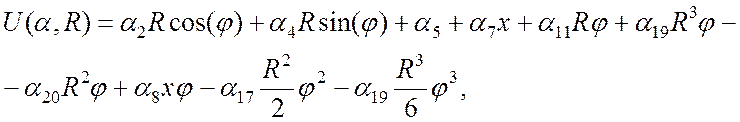
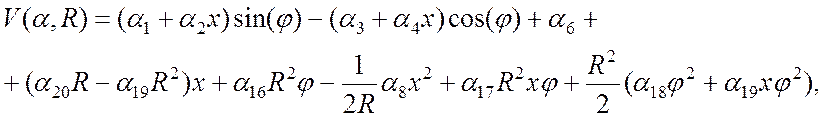                                                                             (18)

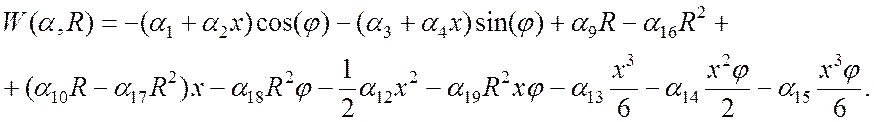
Углы поворота нормалей:

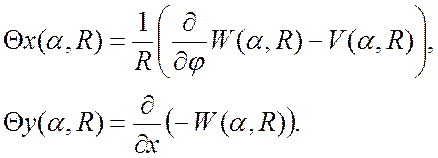                                            (19)

Матрица жесткости.

            Выражения для деформаций срединной поверхности будут следующими:

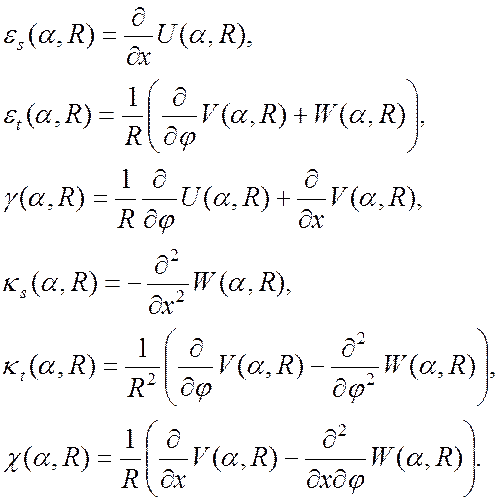                                                                                                                    (20)

            Деформации в матричном виде выглядят следующим образом: , где - коэффициенты при базисных функциях от 1 до 20, B(R) - матрица размером .

Удельная энергия деформации (на единицу площади) выражается через коэффициенты в виде квадратичной формы с матрицей:

                                                                               (21)

где D – матрица упругости материала оболочки размером  (положительно определенная и симметричная).

Матрица жесткости находится интегрированием выражения (21):

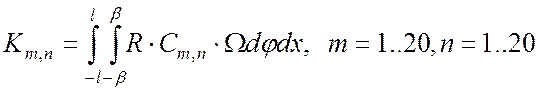                                                                                                                (22)

где  - матрица перехода базисных функций к перемещениям (размером ).

Матрица геометрической жесткости.

            Для вычисления матрицы геометрической жесткости элемента статическое деформирование рассматривается в предположении, что доминирующими являются:

3.  осевые напряжения срединной поверхности,

4.  окружные напряжения срединной поверхности,

5.  напряжение сдвига срединной поверхности.

Нелинейные составляющие соответствующих деформаций определяются следующим образом:

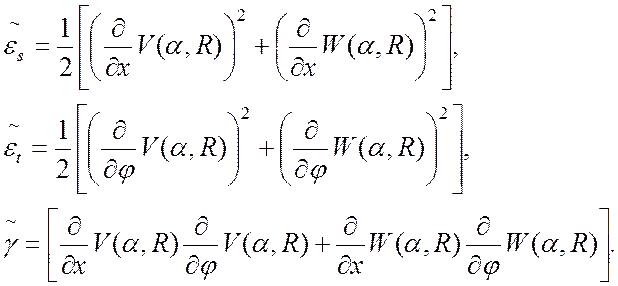               (23)

Нелинейная добавка удельной энергии деформации (на единицу площади) выражается через коэффициенты аппроксимации в виде квадратичной формы: