МКЭ-процессор. Главное окно МКЭ процессора. Подзадачи. Структура данных МКЭ. Решатели. Конечные элементы, страница 11

Структура записи о материалах: стандартная (число слоёв; для каждого слоя – тип материала и 3 угла армирования в градусах).

3 компоненты деформации: мембранные (ES, ET, GST).

Матрица упругости: получается интегрированием матрицы материала в местных осях с исключением обжатия и поперечных сдвигов из условия плоского напряженного состояния.

Структура записи о жесткостях:

Число жесткостных параметров равно числу слоёв.

Жесткостные параметры – толщины слоёв.

Реализация: модуль UMembLamin, класс StiffLaminMembr6s.

Квадратурная формула: Quadrature_Delta_5 (семиточечная).

9.3 Треугольная пластина Зенкевича

Элемент Зенкевича (рисунок 1).

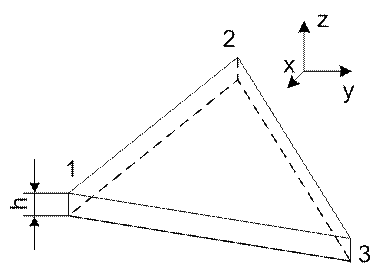
Рисунок 1. Треугольный конечный элемент

5 степеней свободы в узле: US, UT, UN, OS, OT.

Структура записи о материалах: стандартная (число слоёв; для каждого слоя – тип материала и 3 угла армирования в градусах).

6 компонент деформации: мембранные, изгибные, крутильная (ES, ET, GST, KS, KT, X).

Матрица упругости: получается интегрированием матрицы материала в местных осях с исключением обжатия и поперечных сдвигов из условия плоского напряженного состояния.

Структура записи о жесткостях:

Вариант 1. Число жесткостных параметров равно числу слоёв.

Жесткостные параметры – толщины слоёв. Пакет расположен симметрично относительно поверхности приведения в сторону возрастания координаты N.

Вариант 2. Число жесткостных параметров равно удвоенному числу слоёв.

            Жесткостные параметры элемента: 2 числа на слой

1 - толщина слоя

2 - координата N середины слоя от поверхности приведения

Оба варианта реализованы. Вариант устанавливается автоматически по числу жесткостных параметров. Такой избыток требуется для возможности моделирования конструкций с лёгким заполнителем.

Функции формы для мембранных перемещений можно представить следующим образом:

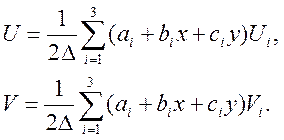                                                                         (1)

Для изгибных перемещений функции формы удобно рассматривать в L – координатах, рассмотрим на примере 1-го узла:

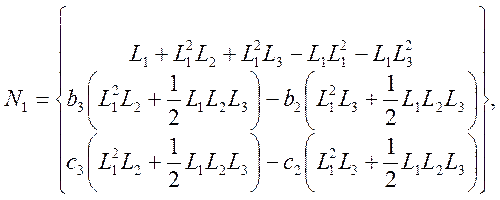                                                                                                                     (2)

где  и т.д.

Остальные две функции формы для узлов 2 и 3 получаются циклической перестановкой индексов .

Матрица жесткости.

Матрица деформаций  может быть найдена следующим образом:

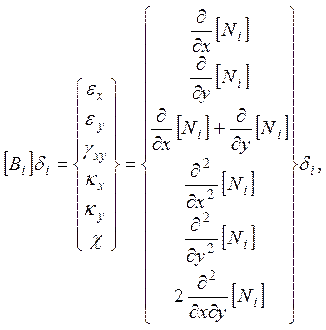                                                                 (3)

где  - деформация растяжения вдоль оси Ox,  - деформация растяжения вдоль оси Oy,  - деформация сдвига в плоскости xOy, - деформация изменения кривизны относительно оси Ox,  - деформация изменения кривизны относительно оси Oy,  - деформация кручения.

Тогда матрица жесткости может быть найдена по известной формуле:

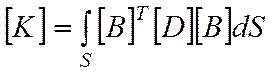                                                         ,                (4)

где [D] – матрица упругости материала.

Матрица геометрической жесткости.

            Для вычисления матрицы геометрической жесткости элемента статическое деформирование рассматривается в предположении, что доминирующими являются:

1.  напряжения растяжения и сжатия в срединной поверхности;

2.  напряжение сдвига срединной поверхности.

Нелинейные составляющие соответствующих деформаций для матрицы  определяются следующим образом:

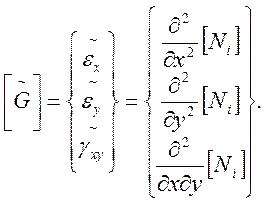                                                                            (5)

Тогда матрица геометрической жесткости может быть найдена по формуле:

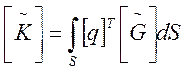                                                                ,                        (6)

где  – вектор погонных сил соответствующих деформациям, и определяемый как произведение средних по элементу напряжений на толщину.

Реализация.

Модуль UshellLamin3, класс StiffLaminShell. Перекрыты процедуры int Calculation(),int ResCalculation(),int UCalculation(TFEResultTab*). В том же модуле реализован элемент – треугольник с 4-мя узлами (полный кубический сплайн) - StiffLaminShell3_1 как производный от StiffElem. В классе перекрыты процедуры int Calculation() и int ResCalculation().

Интегрирование выполняется численно - квадратурная формула: Quadrature_Delta_5.

9.4 Балка Тимошенко

            Балка сплошного прямоугольного сечения. Балка представлена в виде 2-узлового конечного элемента с 6-ю степенями свободы (U_x,U_y,U_z,O_x,O_y,O_z) (рис. 2). Силовые воздействия определяются либо равномерно распределенной нагрузкой вдоль оси балки, либо как сосредоточенные силы с известными точками приложения на оси балки.

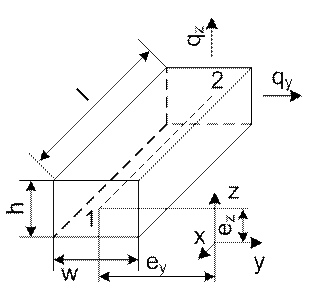
Рисунок 2. Балочный конечный элемент

Обозначено:

l – длина балки;

h и w – соответственно высота и ширина сечения балки;

F – площадь сечения балки;

1 и 2 – номера узлов конечного элемента;

x,y,z – оси  местной системы координат элемента;

e_y,e_z – эксцентриситеты оси балки;

и - компоненты нагрузки;

 – деформация растяжения/сжатия;

 – деформация кручения балки;

 – деформации сдвига оси балки;

 – деформации изменения кривизны оси балки;

U – продольные перемещения;

V,W – поперечные перемещения;

 – угловые перемещения относительно соответствующих осей;

x – линейная координата в продольном направлении.

Основные гипотезы деформирования: статическая – отличны от нуля только напряжения растяжения/сжатия и напряжения поперечного сдвига; кинематическая – плоские до деформации поперечные сечения балки остаются после деформации плоскими, но перестают быть ортогональными к изогнутой оси.

Матрица жесткости.

Деформация растяжения/сжатия и деформация кручения выражаются следующим образом:

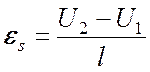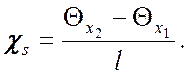                                                   ,           (7)

Деформации сдвига оси балки будут следующими:

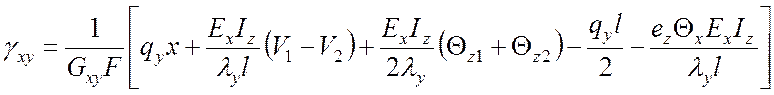,                                                                             (8)