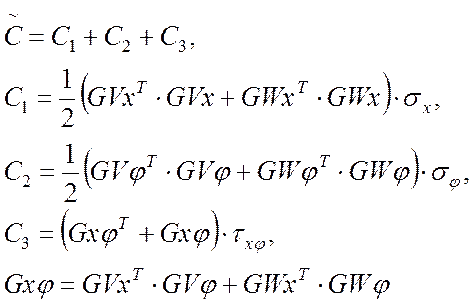МКЭ-процессор. Главное окно МКЭ процессора. Подзадачи. Структура данных МКЭ. Решатели. Конечные элементы, страница 13

                                        .                                                                             (24)

тогда матрица геометрической жесткости в неопределенных коэффициентах:

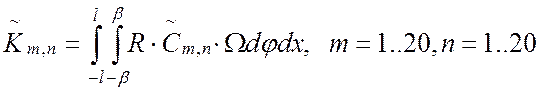                                  .                                                                             (25)

Реализация.

Элемент выполнен в виде класса StiffBakul4Shell (модуль UShellBakul4), перекрыты процедуры формирования матрицы жесткости int Calculation() и вычисления результатов int ResCalculation(). Для расчета нелинейного деформирования оболочки реализован производный от StiffBakul4Shell класс StiffBakul4ShellU (модуль UShellBakul4U), в котором перекрыта процедура формирования матрицы геометрической жесткости int UCalculation(TFEResultTab*).

Введены вспомогательные классы:

class GeomCylElem – класс геометрических параметров цилиндрического элемента оболочки (включает цилиндрические координаты узлов, размеры и радиус, вычисляется по координатам и заданной кривизне);

class C_Int_CylElem – «интеграл в коэффициентах» для цилиндрического элемента (вычисляется аналитически);

class Inv_CA_CylElem – класс «обратная матрица перехода», предназначенный для перехода от неопределенных коэффициентов к узловым неизвестным (вычисляется аналитически, размер 14 на 20);

class El_pot_intgl_bak –матрица жесткости для элемента Бакулина и аналогичных;

class LocalMainBak – матрица перехода для цилиндрического элемента;

class El_matr_C – матрица жесткости в главных осях, хранятся только незакрепленные степени свободы;

class DefCoefBak – «матрица деформаций в коэффициентах» для цилиндрического элемента, размер 6 на 14;

class MatrDefBakPrepared - «матрица деформаций в коэффициентах» для цилиндрического элемента не умноженная на DefCoefBak, размер 14 на 1;

class MatrDefBak – матрица деформаций для цилиндрического элемента;

class MatrNBak – матрица напряжений для цилиндрического элемента;

Для вычисления геометрической матрицы жесткости введены дополнительные классы:

            class UStressAvg – напряжения ;

            class CU_Int_CylElem – «интеграл в коэффициентах» для цилиндрического элемента;

            class CU_Int_GWx, CU_Int_GVx, CU_Int_GWf, CU_Int_GVf – «интегралы в коэффициентах» для GWx, GVx, GWf и GVf, соответственно.

9.6 Трехслойный цилиндрический КЭ (легкий заполнитель)

Трехслойная круговая цилиндрическая оболочка с моментными ортотропными несущими слоями и легким заполнителем, работающим на сдвиг и сжатие в поперечном направлении. Внешняя нагрузка в виде сосредоточенных усилий или поверхностных сил может прикладываться к любому из несущих слоев.

Для моделирования используется цилиндрический 8-узловой 6-гранный конечный элемент, который позволяет точно задать форму цилиндрической оболочки (рисунок 4). Несущие слои могут быть разной толщины и выполнены из различных материалов. Жесткостные характеристики могут меняться от элемента к элементу, что позволяет рассчитывать оболочки с переменной жесткостью в окружном и меридиональном направлениях. Интенсивность распределенной нагрузки, действующей на каждый несущий слой, может быть различной для элементов оболочки.

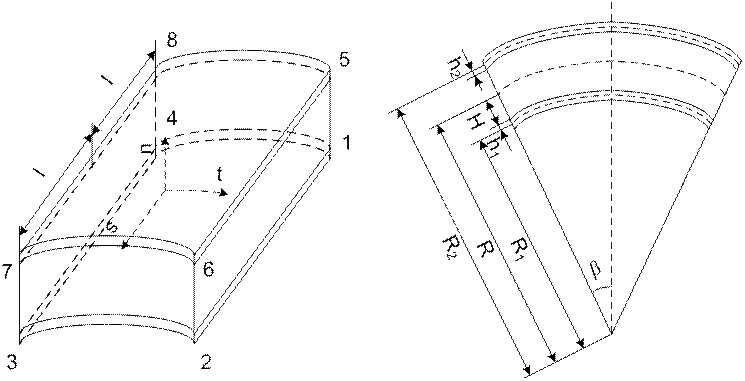
Рисунок 4. Цилиндрический прямоугольный трехслойный элемент

Обозначения:

для внутреннего несущего слоя i=1, для внешнего – i=2;

R₁, R₂, R- радиусы срединных поверхностей внутреннего и внешнего слоев и заполнителя соответственно;

h₁, h₂, H - полутолщины внутреннего, внешнего слоев и заполнителя соответственно.

Упругие константы: E_z, G_xz, G_yz, E_x, E_y, G_xy, E_xy - модули упругости и модули поперечного сдвига для жесткого заполнителя (для легкого заполнителя учитываются только первые три);

 - деформации срединных поверхностей несущих слоев в осевом и окружном направлениях;

 - деформация сдвига срединных поверхностей несущих слоев;

 - деформации изменения кривизн срединных поверхностей несущих слоев;

 - деформации кручения срединных поверхностей несущих слоев;

 - осевые, касательные (по окружности) и радиальные (по нормали) перемещения;

x_i, y_i, x, y - линейные координаты в осевом и окружном направлениях в несущих слоях и заполнителе;

 - угловая координата в окружном направлении.

Связь коэффициентов при базисных функциях с перемещениями координатной поверхности задается в виде (18). Углы поворота нормалей (19). Интерполяция перемещений для внешнего несущего слоя совпадает с (18), но коэффициенты имеют номера с 21 по 40. Всего элемент имеет 40 степеней свободы (по 20 на каждый несущий слой).

Матрица жесткости для несущих слоев.

Выражения для деформаций срединных поверхностей несущих слоев имеют вид (20). Тогда для внутреннего слоя деформации в матричном виде выглядят следующим образом: , где коэффициенты при базисных функциях от 1 до 20, B(R₁) - матрица размером 6х20. Удельная энергия деформации (на единицу площади) выражается через коэффициенты в виде квадратичной формы с матрицей

                                                                                     (26)

где D - матрица упругости материала размером 6х6 (положительно определенная и симметричная). Матрица жесткости находится интегрированием выражения (26):

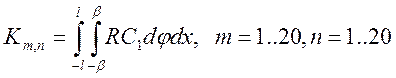                                               .    (27)

Для внешнего слоя (коэффициенты при базисных функциях от 21 до 40) матрица удельной энергии деформации равна

                                                               ,                    (28)

а матрица жесткости

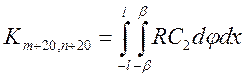                                                           .                 (29)

Матрица жесткости для легкого заполнителя.