Результаты опытных данных, полученные измерением или иным путем сбора первичной информации являются статистическим материалом и подлежат математической обработке. Она выполняется для того, чтобы исследовать полученную информацию на промах и «очистить» ее от грубых ошибок, которые могут существенно исказить истинное значение измеренной величины; определить абсолютную погрешность найденного среднего значения искомой величины (так называемый доверительный интервал); ответить на вопрос: достаточно ли выполненных измерений и их точности для достоверности полученного результата. Если не достаточно, то какими способами можно будет повысить достоверность.
При выполнении расчетного задания 1 его исходные данные сначала проверяют на нормальность распределения ошибок, что позволяет обоснованно применять основные положения теории ошибок для дальнейшей обработки. Затем исходные данные исследуют на промах и по всем правилам освобождают (или не освобождают) от подозрительных величин.
После этого находят среднюю искомую величину и ее ошибку (доверительный интервал) при пяти значениях надежности α, равных 90, 95, 99 %.
На последнем этапе дают ответ: достоверна или нет исходная информация, какими путями ее можно повысить.
Исходные данные: Измерение диаметра стеклянного литого цилиндра штангенциркулем показали следующие результаты (табл.1).
Таблица 1 Результаты измерений.
|
Номера измерений i |
Значение измерений di , мм |
Номера измерений i |
Значение измерений di , мм |
|
1 |
774 |
10 |
774,6 |
|
2 |
774,5 |
11 |
777,7 |
|
3 |
774,3 |
12 |
774,7 |
|
4 |
775 |
13 |
774,8 |
|
5 |
774,9 |
14 |
775,1 |
|
6 |
774,8 |
15 |
775,1 |
|
7 |
774,1 |
16 |
775,0 |
|
8 |
774,2 |
17 |
772,5 |
|
9 |
774,4 |
Задание:
Проверить ошибки измерений на нормальность распределения.
Исследовать полученную информацию на промах при коэффициенте надежности α=0,95
Определить диаметр цилиндра и доверительный интервал (ошибку) при надежности равной 90, 95 и 99%.
Оценить результаты измерений на достоверность и указать способы ее повышения.
Решение:
1. Проверка ошибок измерений на нормальность распределения.
Для разбивки 17 значений на классы находим ориентировочную ширину каждого класса. В нашем случае она составит:
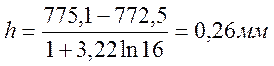 (1)
(1)
Принимаем ширину класса равной 0,3 (соизмеримой с точностью применяемого измерительного средства). Далее составляем табл.2
Таблица.2. Расчет накопленных частостей
|
Номера классов |
Границы классов измеренного диаметра, мм |
Частота попадания в класс |
Накопленная частота в физическом выражении |
Накопленная частота, % |
|
1 |
772,5-772,8 |
1 |
1 |
6,25 |
|
2 |
772,8-773,1 |
0 |
1 |
6,25 |
|
3 |
773,1-773,4 |
0 |
1 |
6,25 |
|
4 |
773,4-773,7 |
0 |
1 |
6,25 |
|
5 |
773,7-774 |
1 |
2 |
12,5 |
|
6 |
774-774,3 |
3 |
5 |
31,2 |
|
7 |
774,3-774,6 |
3 |
8 |
50 |
|
8 |
774,6-774,9 |
4 |
12 |
75 |
|
9 |
774,9-775,2 |
4 |
16 |
100 |
2. Исследование результатов измерений на промах.
Определяем среднее значение диаметра из 17 измерений по формуле.
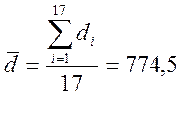 мм
(2)
мм
(2)
Находим среднее квадратическое отклонение σ замеров по формуле.
![]()
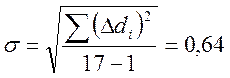 мм
(3)
мм
(3)
Вычисляем значения безразмерного статистического критерия V* относительно подозри-тельной величины d1=76,76 мм. Он будет равен.
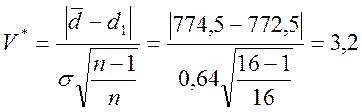
![]() (4)
(4)
Находим максимально-возможное значение V*max. При коэффициенте надежности α=0,95 и числе данных n=16, используя табличные данные получаем V*max=2,52.
Сравнивая V*=3,2 с величиной V*max=2,52 (V*=3,2>V*max=2,52) заключаем, что исследуемые подозрительные значения замеров d1=772,5 мм является промахом, и ее исключаем из выборки.
Исследуем на промах величину d2=775,1 мм.
Среднее значение диаметра из оставшихся 16 замеров составит:
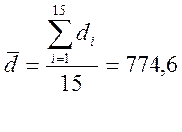 мм. (5)
мм. (5)
Средне квадратичное отклонение замеров.
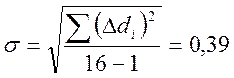
(6)
Значение величины V* относительно второй подозрительной величины d2=775,1 мм.
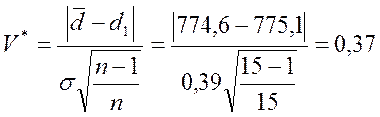
(7)
При α=0,95 и n=15 V*max=2,49
Поскольку V*=0,37< V*max=2,52,то исследуемое подозрительное значение замера d2=76,60 мм не является промахами, и их оставляем для дальнейших оценок.
3. Определение диаметра цилиндра и доверительного интервала при надежности равной 0,90; 0,95 и 0,99.
Среднее арифметическое значение диаметра после «очистки» результатов 16 измерений от промахов равно
![]() мм
мм
Среднеквадратическая ошибка среднего арифметического значения диаметра равна.
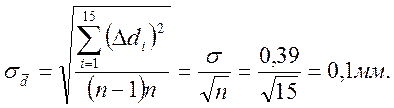 (8)
(8)
Значение коэффициента Стьюдента tαn при надежности α=0,95и n=15равно tαn=2,13
Абсолютная погрешность (доверительный интервал) измерений α=0,95 составит.
![]() (9)
(9)
Результат измерения диаметра при α=0,95:
![]() (10)
(10)
Или 774,39мм<d<774,81
Относительная погрешность измерения при α=0,95:
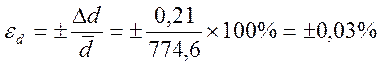 (11)
(11)
Для оценки влияния коэффициента надежности α на показатели статистической обработки выполним аналогичные расчеты при значениях α=0,90; 0,95; 0,99.Результаты расчетов оформляем в виде таблицы 3.
Таблица 3.Показатели статистической обработки измерений диаметра стеклянного цилиндра при разной надежности.
|
Наименование показателей. |
Обозначение. |
Значение показателей при надежности α, равной |
||
|
0,90 |
0,95 |
0,99 |
||
|
Среднее арифметическое значение |
|
774,6 |
774,6 |
774,6 |
|
Среднеквадратическая ошибка среднего арифметического |
|
0,1 |
0,1 |
0,1 |
|
Коэффициент Стьюдента |
tαn |
1,75 |
2,13 |
2,95 |
|
Абсолютная погрешность (доверительный интевал). |
|
0,175 |
0,21 |
0,29 |
|
Результаты измерения |
d, мм |
774,6±0,175 |
774,6±0,28 |
774,6±0,29 |
|
Относительная ошибка доверительного интервала. |
% |
0,02 |
0,03 |
0,04 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.