Методичні вказівки до курсового проектування з дисципліни "Теорія електричного зв'язку", страница 7

Вимоги до пропускної здатності неперервного та дискретного каналів зв'язку у складі цифрової системи формулюються на основі теорем кодування Шеннона для каналів з завадами [1 - 3], відповідно до яких вони повинні перевищувати продуктивності відповідних джерел.

Пропускна здатність неперервного каналу зв'язку визначається формулою Шеннона

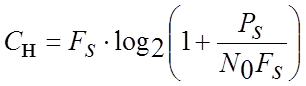,                                                (4.45)

а дискретного – співвідношенням

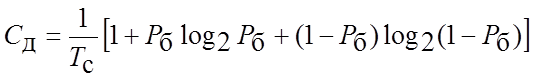,                      (4.46)

до яких входять відповідні характеристики сигналів та завад: середня потужність  і ширина спектру  маніпульованого сигналу, питома потужність білого гаусового шуму , тривалість  та імовірність помилки  двійкового символу (біту).

Відношення , що входить до формули Шеннона (4.45), для АМ-2, коли один із сигналів дорівнює нулю, визначається як

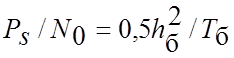                                               (4.47)

або

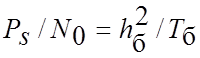                                               (4.48)

для всіх інших видів маніпуляції.

Якщо в системі передачі відсутнє завадостійке кодування, то значення T_с дорівнює тривалості двійкового символу  на виході АЦП. Якщо ж використовується завадостійке кодування, то , де n і k параметри коригуючого коду.

4.6 Показники ефективності цифрової системи зв'язку

Цифрові системи зв'язку характеризуються якісними показниками, основними з яких є швидкість і вірність передачі.

Для забезпечення необхідної швидкості передачі інформації при заданій вірності приходиться витрачати деяку потужність сигналу і займати смугу частот у каналі зв'язку.

Для оцінки ефективності системи зв'язку вводять коефіцієнт використання каналу по потужності b (енергетичну ефективність) і коефіцієнт використання каналу по смузі частот g (частотну ефективність):

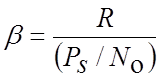,                                                 (4.49)

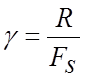,                                                        (4.50)

де R — швидкість передачі інформації;

— відношення сигнал/шум на вході демодулятора;

 — ширина смуги частот, що займається сигналом.

Безрозмірні коефіцієнти b і g мають сенс питомих швидкостей (швидкостей, що віднесені до одному з параметрів каналу). Так, коефіцієнт g визначає швидкість передачі інформації в одиничній смузі частот.

Узагальненою характеристикою є коефіцієнт використання каналу по пропускній здатності (інформаційна ефективність):

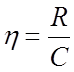.                                                        (4.51)

Для неперервного каналу зв'язку з урахуванням формули Шеннона (4.45) отримуємо наступний вираз:

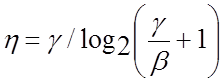.                                          (4.52)

Відповідно до теорем Шеннона [1 – 3] при h=1 можна отримати межеву залежність між b і g:

b=g/(2^g - 1),                                                  (4.53)

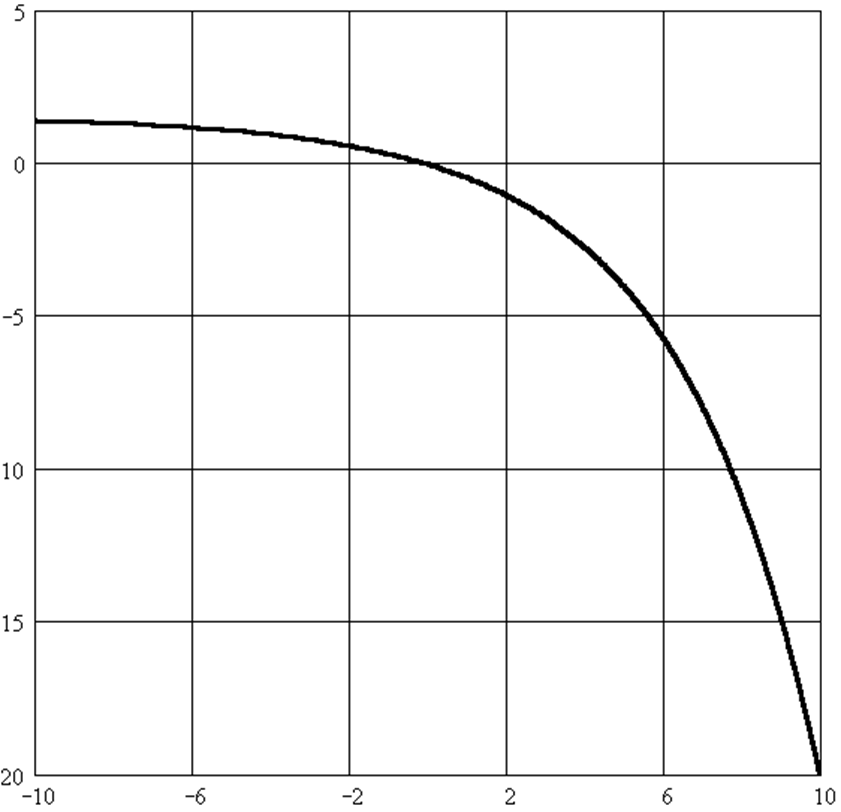
яка має назву межі Шеннона, що відображає найкращий обмін між b і g у неперервному каналі. Цю залежність зручно зобразити у вигляді кривої на площині b- g (рис. 4.4).

Під час побудови графіка граничної залежності ß=f() значення ß і  відкладаються в логарифмічних одиницях - відповідно 10 lg ß та 10 lg  Порівняння розглянутих варіантів передачі між собою та з граничною ефективністю виконуються роздільно за коефіцієнтами ß та . Якщо значення коефіцієнтів ß та  малі (ß<-10дБ і <3 дБ), то необхідно вказати способи підвищення енергетичної та частотної ефективностей.

, дБ

, дБ

Рисунок 4.4 – Межа Шеннона

5 ПІДГОТОВКА ДО ЗАХИСТУ КУРСОВОЇ РОБОТИ ТА ЇЇ ЗАХИСТ

Мета підготовки до захисту курсової роботи полягає в тому, щоб навчитися вірно відповідати на такі основні типи питань:

1. Чому для передачі різних видів повідомлень в останній час, в основному, використовуються цифрові системи зв'язку?

2. Для чого потрібен той чи інший пристрій структурної схеми такої системи?

3. Які міркування враховувались під час визначення характеристик кожного пристрою у складі цифрової системи зв'язку?

4. Як змінюються показники ефективності цифрової системи зв'язку з використанням завадостійкого кодування, іншого методу маніпуляції та способу прийому?

Форма відповіді не регламентується. При відповіді на дві останні категорії питань можна навести потрібні розрахункові формули або дати якісну відповідь - подати суть фізичних процесів, що мають місце в цифрових системах зв'язку. Важливо, щоб студент виявив знання сучасних принципів аналізу, синтезу та оптимізації сигналів, кодів, каналів і систем електрозв'язку, а також практичною реалізації пристроїв, що входять до складу цих систем.

ПЕРЕЛІК ПОСИЛАНЬ

1. Омельченко В.О, Саннiков В.Г. Теорiя електричного зв'язку. Ч. 1, 2, 3. - К.: IСДО, 1994, 1995, 1997.

2. Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи/ Под ред. Д.Д. Кловского. - М.: Радио и связь, 1999.

3. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. - М.: Радио и связь, 1986.

4. Банкет В.Л., Дорофеев В.М. Цифровые методы в спутниковой связи. - М.: Радио и связь, 1988.

5. Прокис Дж. Цифровая связь. - М.: Радио и связь, 2000.

6. Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра. - М.: Радио и связь, 2000.

7. Коржик В.И., Финк Л.М., Щелкунов К.Н. Расчет помехоустойчивости передачи дискретных сообщений: Справочник. - М.: Радио и связь, 1981.

8. Кодирование информации (двоичные коды): Справочник/ Под ред. Н.Т. Березюка. - Харьков: Вища школа, 1978.

9. Розрахунки й оптимізація систем електрозв'язку: Завдання на курсову роботу з дисципліни "Теорія електричного зв'язку" та методичні вказівки до їх виконання/ Укладач П.В. Іващенко. - Одеса: УДАЗ, 1999.

10. Методические указания к курсовой работе по дисциплине "Теория электрической связи"/ Сост. В.Г.Санников. - М.: МЭИС, 1992.

ДОДАТОК А

Функція Крампа