Методичні вказівки до курсового проектування з дисципліни "Теорія електричного зв'язку", страница 5

Якщо в каналі зв'язку не використовується завадостійке (коригуюче) кодування, то допустима ймовірність помилки символу на виході демодулятора дорівнює значенню , що знайдене під час розрахунків характеристик АЦП і ЦАП. З використанням залежності =f() необхідно визначити відношення сигнал/шум для системи передачі без коригуючого кодування , за якого = та показати на графіку значення  і  (рис. 4.3).

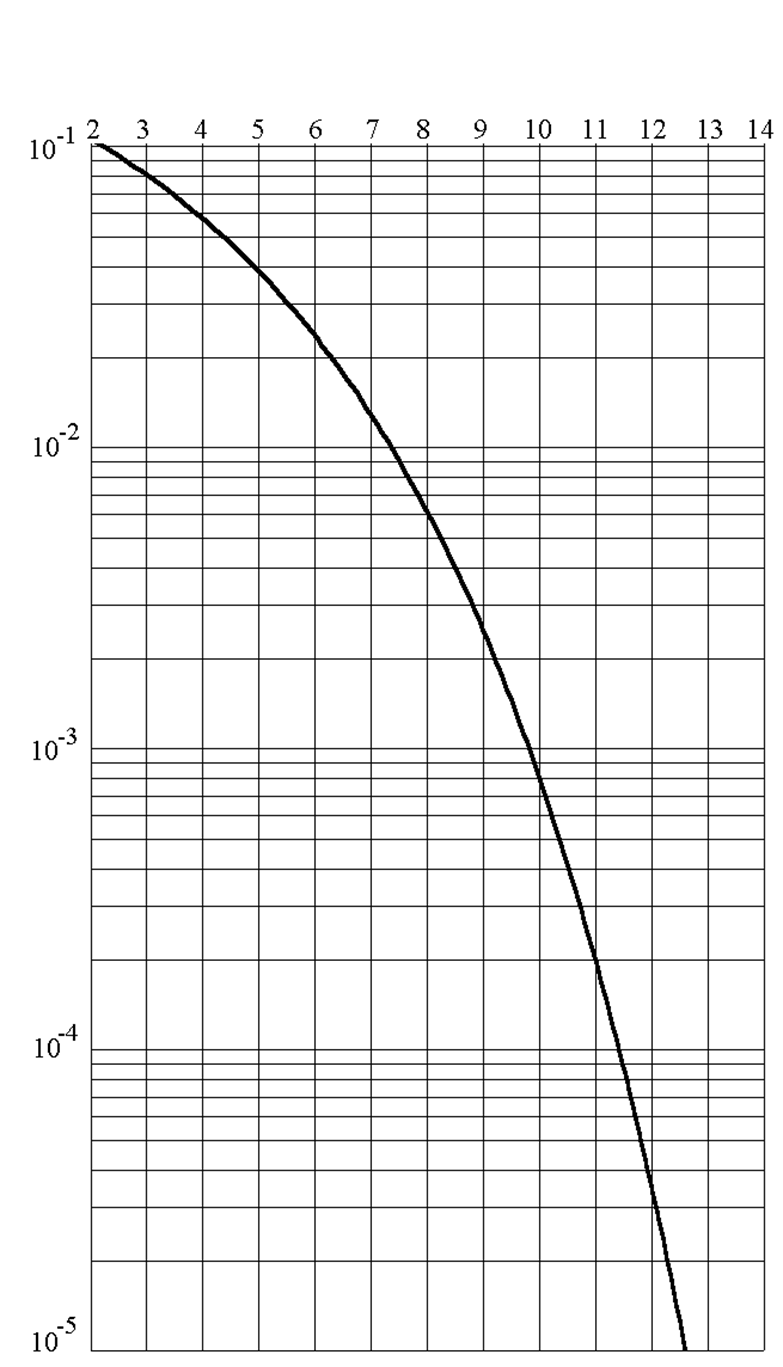
Рисунок 4.3 - Завадостійкість цифрових систем без коригуючого кодуванням таз ним

4.4 Характеристики кодеку завадостійкого коду

Коригуючі (завадостійкі) коди дозволяють підвищити завадостійкість і завдяки цьому зменшити необхідне відношення сигнал/шум на вході демодулятора для заданої ймовірності помилки прийнятих символів. Величина, що показує у скільки разів (на скільки децибел) зменшується необхідне відношення сигнал/шум на вході демодулятора завдяки використанню коригуючого кодування, має назву енергетичного виграшу кодування (ЕВК) .

Канали зв'язку із коригуючим кодуванням і без нього зручно порівнювати, якщо як відношення сигнал/шум використовувати відношення середньої енергії сигналів, що витрачається на передачу одного інформаційного символу (біту), до питомої потужності шуму:  = Е_б/N₀.

Так, якщо в каналі зв'язку без кодування необхідне відношення сигнал/шум для забезпечення заданої імовірності помилки символу  позначити через , а в каналі зв'язку з кодуванням для забезпечення такої ж еквівалентної ймовірності помилки інформаційного символу  - через , то ЕВК  буде визначатися як

D=/ або D [дБ]= [дБ] -  [дБ].                       (4.23)

Еквівалентна ймовірність помилки інформаційного символу  при використанні декодування з виправленням помилок визначається [1 - 8] як

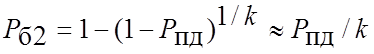,                                 (4.24)

де  - кількість інформаційних символів у кодовій комбінації, що визначається розрядністю АЦП (4.14);

 - ймовірність помилкового декодування кодових комбінацій з виправленням помилок:

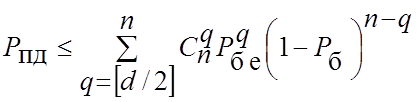.                            (4.25)

Тут

 - мінімальна кодова відстань;

 - символ цілої частини числа;

 - кількість символів (довжина) кодової комбінації;

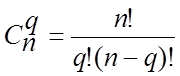                                                 (4.26)

- кількість сполучень з n no q;

 - еквівалентна імовірність помилки двійкового символу на вході декодера, яка залежить від енергетичного відношення 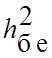 (табл. 4.1). У випадку коригуючих кодів це відношення має значення

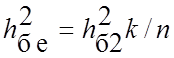,                                                 (4.27)

яке враховує зменшення тривалості символів, що передаються по неперервному каналу зв'язку, через введення в кодові комбінації додаткових символів при кодуванні, і відповідне зменшення енергії сигналу на вході демодулятора (рис. 4.3).

Зв'язок між основними параметрами двійкових коригуючих кодів ,  та  встановлює верхня межа Хеммінга для кількості перевірочних (контрольних) символів кодової комбінації [1 - 3, 6 - 8]

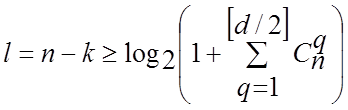,                                     (4.28)

значення якої розраховані у [8] та наведені в табл. Б.1.

При використанні співвідношень (4.23) – (4.28) для розрахунку параметрів коригуючого коду та побудові функціональних схем кодера і декодера потрібно враховувати метод коригуючого кодування. Розглянемо деякі з цих методів [1 - 8].

У цифрових системах зв'язку широко використовуються класичні двійкові блочні коди , для яких правило кодування записується з використанням породжуючої матриці  розміру :

,                                                       (4.29)

або з використанням ортогональної до неї перевірочної матриці  розміру :

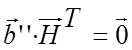.                                                    (4.30)

Тут  - вектор - рядок кодової комбінації примітивного коду довжиною ;

 - вектор - рядок кодової комбінації завадостійкого коду довжиною ;

 - символ транспонування матриці.

Обчислення векторно - матричних добутків та підсумовування за правилами (4.29), (4.30) повинне виконуватися за модулем 2.

Найбільш відомим прикладом двійкових блочних кодів є коди Хеммінга [1 - 8], що мають параметри , , , де  - будь-яке ціле позитивне число. Коди Хеммінга звичайно визначаються перевірочною матрицею , стовпці якої містять всі  ненульових двійкових векторів, наприклад, у вигляді двійкового зображення відповідного номера стовпця.

Якщо до кодів Хеммінга добавити ще один перевірочний символ, який формується шляхом загальної перевірки на парність, то можна отримати коди з параметрами , , .

Іншим прикладом двійкових блочних кодів є коди Ріда - Маллера (РМ) [8], що мають параметри , , 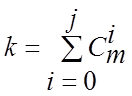, де  - порядок коду (,  - будь-яке ціле позитивне число).

Породжуюча матриця  кодів Ріда - Маллера будується за наступним правилом [8]. У її першому рядку записуються  одиниць. Далі мають місце  рядків, сукупність яких розглядається як матриця розміру , стовпці якої вибираються як двійкові числа, починаючи з нуля, причому нумерація їхніх розрядів робиться зверху вниз. Ці  рядків складають вектори першого порядку. Далі йдуть рядки векторів другого порядку у вигляді всіх можливих порозрядних логічних добутків двох рядків першого порядку, потім - рядки третього порядку у виді всіх можливих порозрядних логічних добутків трьох рядків першого порядку і т.д. Матриця , що побудована у такий спосіб, містить один рядок із всіма одиницями,  рядків першого порядку,  рядків другого порядку,  рядків третього порядку і т.д., тобто загальна кількість її рядків 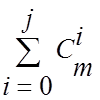 збігається з кількістю інформаційних розрядів .

Прикладом двійкових блочних кодів також є коди Макдональда [8], що задаються за допомогою так званого модулярного зображення, яке вказує для породжуючої матриці  кількості стовпців кожного з  їхніх можливих типів.