Методичні вказівки до курсового проектування з дисципліни "Теорія електричного зв'язку", страница 4

                 ρ=10^0,1ρ[дБ].                                                                                (4.9)

Потужність шуму квантування виражається через величину кроку квантування a [1 - 7]:

               ²_кв=(a)²/12.                                                                            (4.10)

Крок квантування залежить від числа рівнів квантування :

             a=(a_max-a_min)/(L-1).                                                             (4.11)

Тут передбачається, що первинний сигнал a(t), який підлягає перетворенню в цифровий сигнал, приймає значення від a_min до a_max і на інтервалі (a_mln, a_max) підлягає квантуванню. Для сигналів із середнім значенням, що дорівнює нулю a_min=- a_max. Якщо значення a_max не задане, то воно визначається за допомогою співвідношення

                 a_max=П_a,                                                                           (4.12)

де П_а – пік-фактор, який характеризує перевищення максимальним(амплітудним) значенням сигналу його середньоквадратичного значення (кореня із середньої потужності сигналу).

На основі співвідношень (4.10) і (4.11) мінімально можливечисло рівнів квантування визначається як

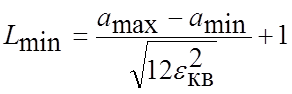                       .                                                    (4.13)

Значність двійкового примітивного коду на виході АЦП

                  k= log₂L                                                                                     (4.14)

єціле число. Тому число рівнів квантування L вибирається яктакий цілий ступіньчисла 2, при якому

                      LL_min.                                                                                 (4.15)

Для визначення припустимої імовірності помилки двійкового символу на вході ЦАП P_б необхідно попередньо визначити припустиму величину потужності шуму хибних імпульсів на основі співвідношення (4.6):

                    ²_х.і.=σ²_ε-²_кв,                                                                     (4.16)

де потужність шуму квантування ²_кв обумовлена співвідношеннями (4.10) і (4.11) при відповідному числі рівнів квантування L. Далі скористаємося співвідношенням [1 - 7], що зв'язує ²_х.і. та імовірність помилки біта на вході ЦАП P_б:

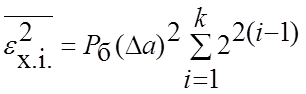                      ,                                                 (4.17)

де величина крокуквантування  визначається формулою (4.11).

Співвідношення (4.17) дозволяє розрахувати припустиму ймовірність помилки символу  на вході ЦАП.

Тривалість двійкового символу (біту) на виході АЦП визначається як

                     Т_б =Т_д/k.(4.18)

4.3 Характеристики модему маніпульованих сигналів

У цифрових системах зв'язку для передачі інформації по радіоканалу використовуються різні методи дискретної модуляції (маніпуляції) гармонічного носія: двійкова амплітудна маніпуляція (АМ-2), двійкова фазова маніпуляція (ФМ-2), двійкова відносна фазова маніпуляція (ВФМ-2), квадратурна відносна фазова маніпуляція (КВФМ), квадратурна відносна фазова маніпуляція зі зсувом (КВФМЗ), двійкова частотна маніпуляція (ЧМ-2), частотна маніпуляція з мінімальним зсувом (ЧММЗ), багаторівневі частотна (ЧМ-М), фазова (ФМ-М), відносна фазова (ВФМ-М) та амплітудно-фазова (АФМ-М) маніпуляції.

Функціональні схеми модуляторів та демодуляторів (детекторів) маніпульованих сигналів, а також часові діаграми, що пояснюють принципи їх роботи, докладно описані в [1 - 7].

Під час передачі маніпульованих сигналів мінімально можлива ширина їх спектра визначається межею Найквіста [1 - 7], яка для АМ-M, ФМ-М, ВФМ-M і АФМ-М має вигляд

,                                                     (4.19)

а для ЧМ-М -

,                                                   (4.20)

де  - тривалість двійкового символу на вході модулятора;

М— число позицій сигналу.

Завадостійкість демодулятора цифрової системи зв’язку визначають імовірністю помилки двійкового символу  (у випадку двійкової маніпуляції) або імовірністю помилки елемента маніпульованого сигналу  (у випадку багаторівневої маніпуляції). Імовірності помилок  і  залежать від методу модуляції, способу прийому, відношення середньої енергії сигналів до питомої потужності завади та характеристик каналу зв'язку.

У табл. 4.1 наведені формули, які визначають імовірність помилки двійкового символу під час передачі сигналами з двійковою та багаторівневою маніпуляцією по гаусовому каналу зв'язку з постійними параметрами [1 - 7]. Для двійкових сигналів значення  і  збігаються. Перерахунок імовірності помилки елемента модульованого сигналу  в імовірність помилки двійкового символу  для сигналів з багаторівневою маніпуляцією зроблено в припущенні, що використовується маніпуляційний код Грея. У всіх формулах прийняті позначення:

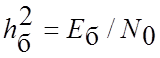 - відношення середньої енергії елементів модульованого сигналу, що витрачається на передачу одного двійкового символу, до питомої потужності шуму;

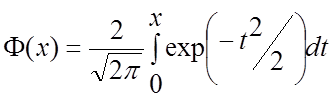                                            (4.21)

 - одна з форм інтегралу ймовірності, що називається функцією Крампа, яка табульована в математичних довідниках та наведена додатку А . Для неї також можна користуватися формулою апроксимації

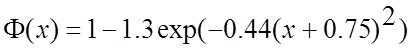.                               (4.22)

Таблиця 4.1 — Імовірність помилки двійкового символу під час передачі маніпульованими сигналами

Спосіб прийому	Вид маніпуляції	Імовірність помилки двійкового символу
Когерентний прийом (КП)	АМ-2
	ЧМ-2
	ФМ-2, ФМ-4
	ВФМ-2, КВФМ, КВФМЗ, ЧММЗ
	ВФМ-4
	АФМ-16
Некогерентний прийом (НП)	АМ-2
	ВФМ-2
	ЧМ-2
	ЧМ-М,

Для заданого методу маніпуляції та способу прийому необхідно розрахувати та побудувати графік залежності  =f(). Під час побудови графіка масштаб для повинен бути логарифмічним, а для значень , що виражені у децибелах ( [дБ] = 10 lg) - лінійним. Під час розрахунків збільшують  з кроком 1 дБ, починаючи з 2 дБ, до такого значення, коли імовірність  не виявиться меншою за . Приклад залежності =f() для когерентного приймання сигналів з ФМ-2 поданий на рис. 4.3.