Методичні вказівки до курсового проектування з дисципліни "Теорія електричного зв'язку", страница 6

Нехай  - спеціальна матриця розміру 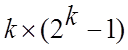, що містить як стовпці всі можливі вектори - двійкові числа, крім нуля, причому нумерація їхніх розрядів відбувається знизу нагору. Її -й стовпець можна розглядати як стовпець типу , а код задавати вектором , утвореним  позитивними цілими числами: 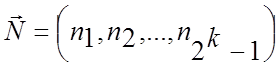, де  - число стовпців типу .

Двійкові  коди Макдональда, модулярне представлення яких складається з  нулів і наступних за ними  одиниць, мають найбільшу кодову відстань . Параметри таких кодів приведені в табл. Б.2.

Матриця - добуток транспонованої спеціальної матриці  на породжуючу матрицю  коду Макдональда містить як рядки усі можливі ненульові кодові вектори..

Спрощення кодера та декодера можна досягнути при використанні циклічних кодів [1 - 8]. Їх кодові комбінації зручно розглядати у вигляді деякого формального полінома ступеня  від перемінної :

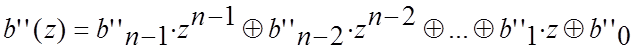,             (4.31)

де  - двійкові символи кодової комбінації,  - знак додавання за модулем 2. Зображення кодових комбінацій циклічного коду в такій формі дозволяє звести дії над ними до дій над поліномами. При цьому додавання двійкових поліномів зводиться до додавання за модулем 2 коефіцієнтів при рівних ступенях перемінної , множення виробляється за звичайним правилом перемножування статечних функцій з обліком того, що отримані коефіцієнти при кожному ступені складаються за модулем 2, а поділ виконується за правилами поділу ступеневих функцій, причому операції вирахування заміняються операціями підсумовування за модулем 2.

Основна властивість циклічних кодів, яка визначила їхню назву, полягає в тому, що для дозволеної кодової комбінації  циклічна перестановка символів  знову призводить до дозволеної кодової комбінації. Зображення кодових комбінацій циклічного коду у вигляді формальних поліномів зручно ще і тим, що така циклічна перестановка рівносильна добутку полінома кодової комбінації  на змінну .

Правило кодування для циклічних кодів засновано на використанні породжуючих поліномів

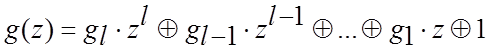,                         (4.32)

що є незвідними, тобто не можуть бути представлені у вигляді добутку поліномів нижчих ступенів. Такі поліноми поділяються тільки на себе чи на одиницю, причому вони поділяють без залишку біном . Такі незвідні поліноми [8] наведені в табл. Б.3 у вісімковій системі обчислення. Так, поліном ступеню , який записаний в табл. Б.3 числом 45, зображує двійкову послідовність

,

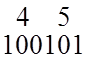а сам поліном записується як

.

Для отримання кодової комбінації циклічного коду з класу лінійних двійкових блокових систематичних кодів поліном примітивного безнадмірного двійкового коду

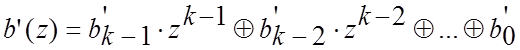                          (4.33)

збільшується на  і до добутку  додається залишок  від розподілу цього добутку виробляючий поліном :

.                                            (4.34)

При такому правилі кодування інформаційні символи займають  старших розрядів кодової комбінації, а інші  розрядів приділяються під перевірочні.

За параметрами до досконалих кодів, у яких нерівність (4.28) переходить у рівність і при цьому мінімізується число додаткових символів  при фіксованих значеннях k і , близькі циклічні коди Боуза-Чоудхурі-Хоквінгема (БЧХ). У кодів БЧХ основні параметри пов'язані співвідношеннями:

,                                                            (4.35)

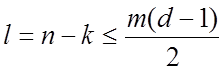,                                                   (4.36)

де  - будь – яке ціле число.

Коди БЧХ мають непарні значення кодової відстані . Їх породжуючий поліном  є найменшим загальним кратним (НЗК) так званих мінімальних поліномів , які відповідно до [8] наведені в табл. Б.4 у вісімковій системі обчислення.

4.5 Інформаційні характеристики джерел повідомлень і каналів у складі цифрової системи зв'язку

Однією з основних інформаційних характеристик неперервного джерела повідомлень є епсілон - ентропія  [1 - 7], яка при умові, що помилка відновлення на виході системи є гаусовою з заданою дисперсією , обчислюється за формулою

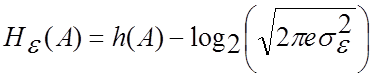,                                     (4.37)

де  - диференційна ентропія, яка залежить від виду розподілу ймовірностей  і дисперсії (середньої потужності) 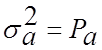 неперервного повідомлення . Відповідні розрахункові формули для її обчислень у випадку типових розподілів ймовірностей наведені в табл. 4.2.

Таблиця 4.2

Коефіцієнт надмірності неперервного джерела  обчислюється за формулою

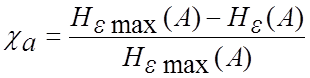.                                     (4.38)

У цю формулу підставляються обчислене значення епсилон-ентропії Н_ε(A) і максимально можливе значення Н_{ε max}(A), яке досягається у випадку гаусового розподілу ймовірності повідомлення a(t) з тією ж дисперсією .

Продуктивність неперервного джерела R_a=Н’_ε(A), яку називають епсилон-продуктивністю, обчислюють у припущенні, що відліки слідують через інтервал дискретизації Котельнікова:

.                                         (4.39)

У цій формулі  - максимальна частота спектру неперервного повідомлення.

Квантованийсигнал 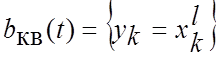 єдискретним за рівнем і ентропія його джерела H(B) у припущенні, що сформовані вАЦП відліки незалежні, обчислюється за формулою ентропії джереладискретних незалежних повідомлень [1 – 7]:

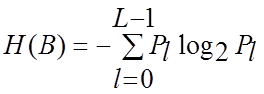.                                         (4.40)

Імовірності  квантованих значень, що входять в цю формулу, можна визначити як

,                                                  (4.41)

де

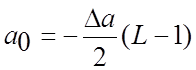, ,                       (4.42)

- квантоване значення сигналу на -ому рівні квантування;

 - щільність ймовірності неперервного повідомлення ;

 - крок квантування.

Коефіцієнт надмірності такого дискретного джерела  обчислюється за формулою

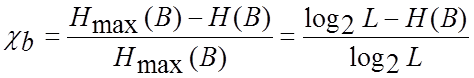.                          (4.43)

Його продуктивність або швидкість вводу інформації у ДКЗ  визначається співвідношенням

,                                           (4.44)

де  - інтервал дискретизації.