Пусть имеются два подобных между собой течения несжимаемой жидкости, запишем для них уравнения сплошности и движения


Из условия подобия процесса течения вытекают очевидные соотношения
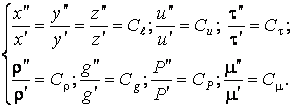
Воспользуемся соотношениями системы и выразим все переменные для второго течения через переменные первого
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Подставим переменные второго течения, выраженные через переменные первого и коэффициенты преобразования подобия в систему уравнений, описывающих второе течение
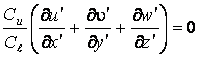 ,
,
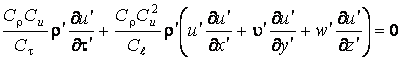 ,
,
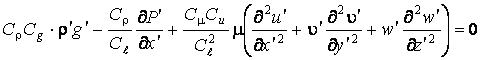 .
.
Таким образом, оба подобных течения описаны системами уравнений, выраженные через переменные, относящиеся к первому течению. Мы уже отмечали выше, что такое возможно лишь при тождественности этих уравнений. Для этого необходимо, чтобы комплексы, составленные из констант подобного преобразования, в последнем уравнении сократились. Это даст нам ряд ограничительных условий, выполнение которых необходимо для установления факта подобия. Из уравнения сплошности будем иметь
![]() .
.
Для выбора констант подобия это
соотношение ограничительных условий не дает, ибо уравнения сохраняют свою
тождественность при любых значениях отношения ![]() .
.
Действительно, т.к. ![]() по физическому смыслу и
по физическому смыслу и ![]() для двух подобных течений, то на эту
величину можно сократить, и уравнение сплошности для второго явления
естественным образом преобразуется в уравнение сплошности и для первого явления
для двух подобных течений, то на эту
величину можно сократить, и уравнение сплошности для второго явления
естественным образом преобразуется в уравнение сплошности и для первого явления
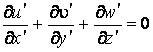 .
.
Из уравнения движения следует
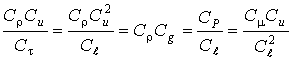 .
.
Рассмотрим члены этого соотношения попарно
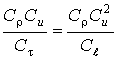 или
или 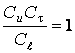 ;
;
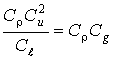 или
или  ;
;
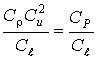 или
или 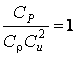 ;
;
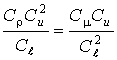 или
или 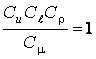 .
.
Полученные равенства могут быть представлены в виде критериев подобия. Для чего вместо констант подобия необходимо подставить их отношения величин и сгруппировать величины по индексам
![]() , откуда
, откуда ![]() ;
;
![]() – критерий гомохронности.
– критерий гомохронности.
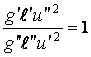 ;
; ![]() ;
;
![]() – критерий Фруда.
– критерий Фруда.
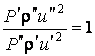 ;
; 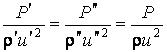 ;
;
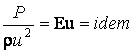 – критерий Эйлера.
– критерий Эйлера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.