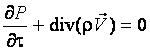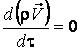Комбинирование критериев и относительных переменных. Сплошная среда и краевая задача, страница 4

; .

Уравнение состояния

.

Зависимость физических свойств жидкостей (газов) от температуры и давления

; ; .

Для решения краевых задач данного типа необходимо задать краевые условия.

1.  Геометрические условия, характеризующие форму и размер тела, омываемого жидкостью.

2.  Граничные условия – распределение скорости, давления и температуры на поверхности тела  во входном и выходном сечениях канала.

В соответствии с формализмом Прандтля, скорость на поверхности тела равна нулю

.

При течении жидкости и газа по каналам граничные условия для температурного поля могут быть заданы в виде функции изменения температур на поверхности тела (граничные условия первого рода)

,

или в виде задания характера распределения плотности теплового потока на поверхности (граничные условия второго рода)

.

3.  Начальные условия, характеризующие распределение скорости, температуры и давления в начальный момент времени при :

; ;.

Для установившегося, стационарного случая граничные условия со временем остаются неизменными, а начальные условия при этом нужны.

          Используя гипотезу Био-Фурье для теплопроводности в слое неподвижной жидкости (газе) в непосредственной близости у поверхности

,

где  – внешняя нормаль к поверхности тела; и гипотезу Ньютона о плотности теплового потока, передаваемого в процессе теплоотдачи,

,

откуда в общем случае коэффициент теплоотдачи равен

.

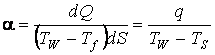Получим дифференциальное уравнение теплообмена

.

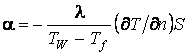Гидромеханическое подобие

          С целью некоторого количественного сокращения необходимого анализа упростим несколько задачу. Будем рассматривать несжимаемую жидкость, для которой . В этом случае уравнение неразрывности

может быть сведено к виду

;

и его можно вынести за знак оператора и сократить

 или

распишем операцию

,

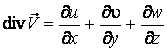где . Уравнение движения для сокращения выкладок запишем лишь в проекции на ось

.

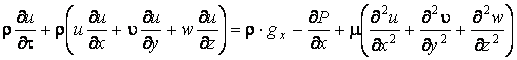Сделано предложение о постоянстве динамической вязкости.