Комбинирование критериев и относительных переменных. Сплошная среда и краевая задача, страница 3

          Конвективный теплообмен – это процесс переноса тепла в жидких и газообразных средах с неоднородным распределением температуры, скорости, плотности при конечном перемещении макрообъемов в сплошной среде.

Математическое описание конвективного теплообмена

          Исследование процессов теплообмена в подавляющем большинстве случаев базируется на феноменологическом подходе. Теплоноситель при этом рассматривается как сплошная среда. Причем его молекулярная структура не анализируется, а интенсивность микроскопического переноса энергии в форме тепла учитывается параметрами, определяющими теплофизические свойства вещества:  – вязкость,  – теплопроводность,  – плотность,  – изобарная теплоемкость. Их считают заданными, используя для численного определения соответствующие справочные материалы. В основу математического описания положены хорошо проверенные физические законы: первое начало термодинамики, закон сохранения вещества, закон сохранения импульса. Для замыкания систем уравнений обычно используют уравнение состояния, уравнение термодинамического процесса, в качестве которого чаще всего используют уравнение Пуассона. В случаи теплообмена системы дифференциальных уравнений замыкают используя гипотезы Био-Фурье (о пропорциональности вектора плотности теплового потока градиенту температуры) и гипотезы Ньютона (о пропорциональности касательного напряжения трения поперечному градиенту скорости)

.

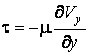В рамках развиваемого феноменологического подхода процесс переноса энергии в форме тепла – процесс теплообмена однозначно определяется полями: скорости – , давления – , температуры –  в зависимости от координат (, , ) и времени . Для определения пяти неизвестных: трех компонент скорости (, , ), давления и температуры необходимо иметь пять уравнений. Не акцентируя внимание на процессе выхода этих уравнений, запишем их для ортогональной декартовой системы координат. Для однофазной химически однородной изотропной несжимаемой жидкости система уравнений имеет вид:

          уравнение энергии

,

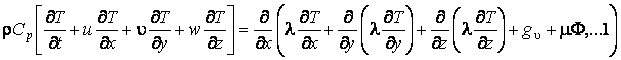где:  – соответствующие вектора скорости на оси  – соответственно; – плотность тепловыделения внутренних источников тепла;  – диссипативная функция – функция распределения механической энергии потока

.

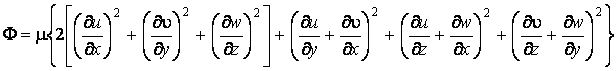Уравнения движения жидкости (газа) в проекциях на оси  (закон сохранения импульса) в форме уравнений Навье-Стокса

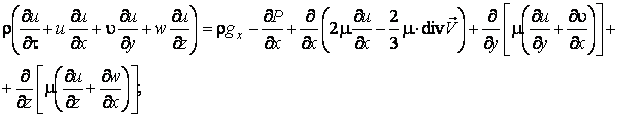
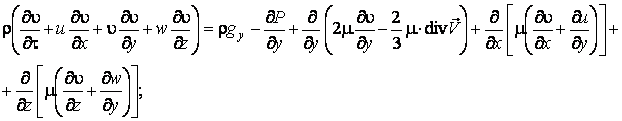
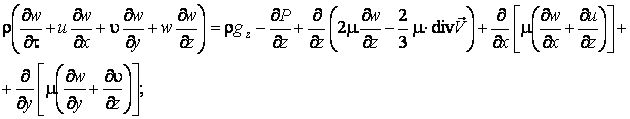
где:  – проекции вектора ускорения свободного падения на соответствующие оси. Уравнение сплошности (неразрывности) среды: