![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Запишем безразмерные комплексы
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
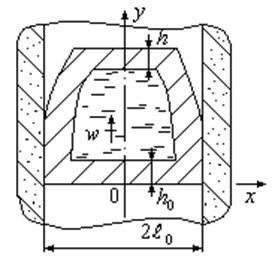
Можно проанализировать полученные безразмерные
комплексы и их комбинации: ![]() – симплекс,
характеризующий загрязненность отливки вторичными шлаками;
– симплекс,
характеризующий загрязненность отливки вторичными шлаками; ![]() – симплекс, характеризующий
безразмерную толщину оксидной плены;
– симплекс, характеризующий
безразмерную толщину оксидной плены; ![]() – относительная
плотность вторичного шлакового образования;
– относительная
плотность вторичного шлакового образования; ![]() –
скорость движения расплава;
–
скорость движения расплава; ![]() – толщина
оксидной плены;
– толщина
оксидной плены; ![]() – толщина плены в момент,
принятый за начало движения.
– толщина плены в момент,
принятый за начало движения.
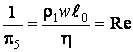 – критерий Рейнольдса;
– критерий Рейнольдса; 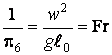 – Критерий Фруда;
– Критерий Фруда; 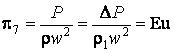 – критерий Эйлера;
– критерий Эйлера; 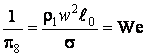 – критерий Вебера. Рассмотрим
произведение
– критерий Вебера. Рассмотрим
произведение
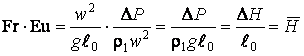 ,
,
где
![]() – потери напора, а
– потери напора, а ![]() – относительная безразмерная
величина потерь напора.
– относительная безразмерная
величина потерь напора.
Таким образом, через безразмерные комплексы функциональная зависимость может быть представлена в виде
![]() .
.
Или, решая его в явном виде относительно симплекса, характеризующего загрязненность отливки вторичными шлаками, получим
![]() ,
,
где
![]() – экспериментальный коэффициент;
– экспериментальный коэффициент; ![]() – показатели степени.
– показатели степени.
По
мнению автора [7] последнее выражение представляет собой частное решение закона
шлакообразования в алюминиевых и магниевых сплавах. Величины ![]() могут быть найдены на основании
обобщения, результаты которого, представленные в логарифмических координатах
могут быть найдены на основании
обобщения, результаты которого, представленные в логарифмических координатах ![]() , хорошо укладываются на прямые.
, хорошо укладываются на прямые.
Процесс
шлакообразования начинается, когда ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
а критерии
,
а критерии ![]() и
и ![]() имеют
критические значения. Анализ данных совместно с выражением
имеют
критические значения. Анализ данных совместно с выражением ![]() дают возможность получить
безразмерный комплекс
дают возможность получить
безразмерный комплекс
![]() , где
, где 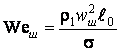 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.