



ЛЕКЦИЯ 15
Элементы теории подобия в краевых задачах тепломассообмена
15.1. Понятие о краевых задачах в сплошной среде
Под сплошной средой понимается непрерывный вещественный континуум, находящийся в жидком, газообразном или твердом состоянии. Такая модель не находится в противоречии с реальной физической дискретностью пока собственные размеры изучаемых систем несоизмеримо больше с величиной частиц, из которых состоит среда (молекула) или длин их характерных перемещений (длин свободного пробега молекул). Это позволяет привлекать для описания протекающих в сплошной среде процессов аппарат дифференциальной и интегральной математики. Каждая из величин, характеризующих явление, в любой точке пространства в каждый момент времени имеет конкретное численное значение. Совокупность ее для всего пространства, охваченного изучаемым процессом, называется полем этой величины: поле скоростей, поле давлений, поле температуры. Физический процесс можно считать изученным, если в любой момент времени нам будут известны поля всех переменных. возможность определения пространственно временного распределения переменных определяет наибольшую полноту знаний о явлении, являющуюся конечной целью любого количественного исследования.
Условие правильно поставленной физической задачи должно содержать полный объем исходных данных, необходимых для выполнения однозначности решения. Обычно эти данные, как уже отмечалось ранее, представлены в виде системы уравнений и условий однозначности.
Основные уравнения определяют внутренний механизм изучаемого явления. Они по своей сути являются выражением наших представлений о взаимодействии элементов фазы между собой и предопределяют развитие процессов, ибо устанавливают связь между физическими условиями в данный момент и их изменениями во времени.
Элементы среды, находящиеся непосредственно на поверхности, взаимодействуют не только между собой, но еще и с окружающими ее телами или, как принято говорить, с элементами окружающей среды. Внешнее влияние не может быть учтено основными уравнениями. Однако они, проникая внутрь явления, накладывают свой отпечаток на ход развития процессов. Мы уже говорили, что совокупность сведений, задаваемых дополнительно к основным уравнениям и определяющих обстановку на поверхности принято называть граничными условиями.
Основные уравнения совместно с известными граничными условиями позволяют найти любое последующее состояние системы по известному предшествующему. Это требует необходимость известности состояния системы в некоторый момент времени, который обычно принимают за начальный момент. Совокупность сведений, определяющих состояние системы в начальный момент, называют начальными условиями. Совокупность начальных и граничных условий, обуславливающих единственность решения рассматриваемой задачи, обычно называют краевыми условиями. А задачи такого типа также называются краевыми.
Обобщенное решение краевых задач, играющих громадную роль практически во всех прикладных проблемах, обычно представляется в виде уравнения
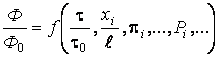 ,
,
где
![]() – искомая переменная,
– искомая переменная, ![]() – определяющий размер,
– определяющий размер, ![]() – время,
– время, ![]() –
координаты,
–
координаты, ![]() – безразмерные комплексы,
– безразмерные комплексы, ![]() – параметрические критерии. Индексом
«0» обозначены значения величин, заданных по условию и играющих роль масштабов,
с помощью которых образуются относительные величины.
– параметрические критерии. Индексом
«0» обозначены значения величин, заданных по условию и играющих роль масштабов,
с помощью которых образуются относительные величины.
15.2. Температурное поле твердого тела
Рассмотрим процесс перераспределения теплоты в твердом теле, исследование которого приводит к типичной краевой задаче, характерной тем, что она может быть решена достаточно точно чисто аналитически даже для тел сравнительно сложной геометрической формы. Сама модель твердого тела, как известно, исключает возможность появления деформации, а, следовательно, определяет отсутствие взаимных перемещений отдельных его частей относительно друг друга. Это приводит к тому, что рассматриваемая задача развивается в неподвижной среде. Следовательно, количественная картина процесса в полной мере будет определяться полем одной физической величины – температуры. Если задано поле температуры, то в этом случае поле потоков тепла будет однозначно определено через векторное поле градиентов температуры. Тогда в рассматриваемой задаче определяющим будет одно дифференциальное уравнение, связывающее температуру с координатами точек пространства, занимаемого твердым телом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.