Элементы теории подобия в краевых задачах тепломассообмена, страница 2

         Ранее мы уже отмечали, что при наличии температурной неравномерности в твердом теле возникающие потоки тепла рассчитываются в соответствии с известной гипотезой Фурье

,

где  – вектор плотности теплового потока, Вт/м²;  – теплопроводность материала, из которого изготовлено твердое тело, Вт/мК;  – температура, К; – символ векторного оператора-градиента.

         Процесс распространения тепла в твердом теле определяется характером распределения температуры  и теплофизическими свойствами самого тела , которые в общем случае изменяются с изменением температуры.

Очевидно, что в основу интересующего нас процесса целесообразно положит уравнение, определяющее температуру как функцию координат и времени.

         Предположим, что материал, из которого изготовлено твердое тело, однороден, а само тело изотропно. Выделим внутри тела элементарный объем, размеры которого настолько малы, что температура на его поверхности практически одинакова. Состояние этого элемента может измениться под воздействием с окружающими его элементами твердого тела, если их температура будет отлична

.

         Обмен энергией в форме тепла приведет к изменению внутренней энергии выделенного объема (элемента). Если единственным энергетическим воздействием на выделенный элемент является теплообмен, то в этом случае в соответствии с первым началом термодинамики изменение внутренней энергии выделенного элемента равно энергии в форме тепла, которым он обменивается с окружающей средой.

.

Распишем составляющие этого равенства.

         Изменение внутренней энергии

.

         Элементарное количество теплоты, подводимое к выделенному элементу или отводимое от него,

,

где  – оператор Лапласа;  – объем выделенного элемента, м³;  – теплоемкость тела, Дж/кг·К;  – плотность, кг/м³. После подстановки равенство может быть сведено к известному уравнению теплопроводности

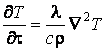 или ,

где 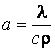 – коэффициент температуропроводности.

         Последнее уравнение позволяет установить соответствие, заключающееся в том, что коэффициент температуропроводности характеризует способность вещества реагировать изменением температуры на факт прохождения энергии в форме тепла. Оно (соответствие) состоит в том, что темп изменения температуры во времени растет вместе с кривизной ее распределения вдоль каждой из координатных осей. При этом производная температуры по времени связана с частными производными по координатам через множитель пропорциональности  – коэффициент температуропроводности.