Получение критериальных эмпирических зависимостей

ЛЕКЦИЯ 11

Получение критериальных эмпирических зависимостей

         Для того, чтобы результаты опытов можно было распространять на все подобные между собой физические процессы в соответствии со второй теоремой подобия, их обработка должна вестись в критериях подобия. Предположим, что зависимость, описывающая процесс теплообмена, представляется степенной функцией

,

где , и  являются постоянными числами.

Такого рода зависимости теоретически не могут быть обоснованы и являются чисто эмпирическими. Как уже отмечалось, они применимы в пределах изменения аргументов, подтвержденных опытами. При их применении не допустимы как экстраполяция, так и интерполяция в непроверенной опытами области изменения аргументов.

Рассмотрим сначала, как получится зависимость вида

.

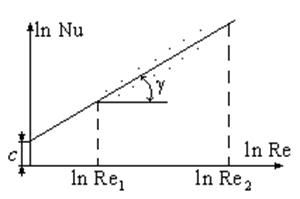
         Из опытных данных находятся числа Рейнольдса  и соответствующие им значения числа Нуссельта . Если приведенная выше зависимость справедлива, то в логарифмических координатах  все опытные точки должны лежать на одной прямой. Прологарифмируем приведенную зависимость

,

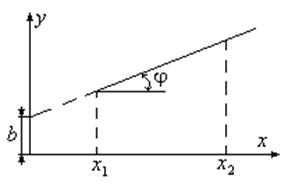
то есть мы получили уравнение прямой вида , где  – есть тангенс угла наклона прямой к оси абсцисс. Постоянная  определяется из соотношения , которому удовлетворяет любая точка прямой.

         Если результаты опытов располагаются по кривой, то кривую разбивают на участки, где они ложатся на отрезки прямой. То есть кривую линию заменяют ломаной прямой.

Если , то .

 Если , то .

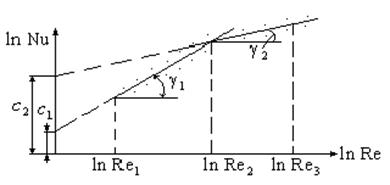
         В случае, если искомая величина является функцией двух аргументов,  на графике  получается семейство прямых. Второй аргумент в этом случае берется в качестве параметра .

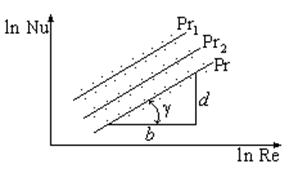
         По любой из параметрических прямых определяется показатель степени при числе Рейнольдса . Затем опытные данные перестраиваются в координатах

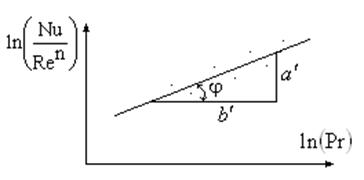
 и по тангенсу угла наклона прямой определяют показатель степени критерия Прандтля, а затем по критериальному уравнению определяют значение коэффициента .     

.

ЛЕКЦИЯ 12