Получение критериальных эмпирических зависимостей, страница 4

; ; ; .

         Рассмотрим закон подобия Коши. Для упругих сил справедлив закон Гука  и существует известный коэффициент подобия , где Е – модуль упругости;  – нормальное напряжение, а  – относительная деформация. При этом Ньютоновский закон подобия

,

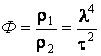переходит в закон подобия Коши

.

Из закона подобия Коши вытекает закон подобия для статики, известный как закон подобия Гука. В случае работы оригинала и модели в области упругих сил обязательно выполняется равенство коэффициентов Пуассона модельной системы и натуры

.

Соответствующий этому равенству критерий подобия называется числом Гука Н

.

Этот закон позволяет получать напряженное состояние твердых тел с помощью прозрачных моделей. Особенно эффективен он при изучении напряженного состояния деталей сложной формы. При этом из прозрачного материала изготавливают геометрически подобную модель, а затем к ней прикладывают такие же внешние механические условия, как к натуре. Под действием возникающих механических напряжений нарушается бывшая изотропность прозрачного материала и возникает двойное лучепреломление. Если поместить такую модель в оптическую систему со скрещенными поляризующими фильтрами, то можно наблюдать интерференционную картину, показывающую распределение упругих напряжений внутри детали.

12.3. Временной масштаб модельных экспериментов

         Моделирование открывает перед исследователем возможность изменения в опытах не только геометрических, но и временных масштабов. Если в законах подобия, описывающих систему, все инварианты подобия равны единице, за исключением временного коэффициента и коэффициента длин, то можно обосновать следующее соотношение

, ,

где .

Это означает, что в уменьшенных моделях все динамические процессы протекают в  раз быстрее. Это позволяет изучать на моделях явления, которые в реальных системах начнутся в отдаленном будущем. Такой прием особенно важен в процессе создания самоорганизующихся вычислительных систем.