Получение критериальных эмпирических зависимостей, страница 3

.

         Если в модели соблюсти равенство полей температуры () и использовать при моделировании ту же жидкость, что и на натурном объекте (воздух), то очевидно можно считать одинаковыми их теплофизические свойства. В этом случае равенство критериев Прандтля достигается однозначно. Что же касается критерия Грасгофа, то его равенство будет достигнуто, если выполнить следующее условие

.

Это позволит нам по известным напряженностям гравитационных полей луны  м/с² и земли  м/с² установить соотношения для сходственных размеров модели и натурного объекта

.

Вычисления дают . Геометрические размеры модели должны быть в 1,82 раза меньше геометрических размеров объекта, это обеспечит выполнение условия геометрического подобия.

         При моделировании более сложных явлений могут возникнуть дополнительные условия, ограничения. Допустим, теплообмен происходит в условиях свободного вынужденного течения. Это приводит к тому, что на свободную конвекцию накладывается вынужденная конвекция. Тогда кроме ранее приведенных равенств, обеспечивающих подобие свободной конвекции, необходимо еще обеспечить для подобия равенства критерия Рейнольдса

.

Тогда для приведенного выше примера получим

.

Выразим отношение скоростей модели и натуры

 или .

То есть при моделировании для обеспечения соблюдения условия кинематического подобия, скорость потока на модели должна быть в 1,82 раза больше, чем на натурном объекте.

12.2. Приближенное моделирование

         Совокупность всех ограничительных условий часто при практическом осуществлении моделирования создает непреодолимые трудности, что делает точное моделирование невозможным. Приходится прибегать к приближенному моделированию.

         Возможности приближенного моделирования расширяются за счет учета удельного веса влияния на процесс различных критериев подобия. Если влияние какого-либо критерия подобия несущественно, то его можно исключить при моделировании, снимая определенные ограничительные условия.

         Необходимость соблюдения определяющего критерия  ответственного за соблюдения подобия тепловых полей, допуская в принципе замену одной жидкости другой, по существу весьма серьезно ограничивает такую возможность

; .

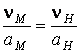         Рассматривая второе соотношение и подставляя в него численные значения для воды и газов нетрудно показать, что вода примерно при температуре, расположенной в диапазоне ^оС, имеет числа  примерно равные числам Прандтля для газов. Таким образом заменить газ модельной жидкостью (водой) при изучении несжимаемых газовых потоков возможно в том случае, если вести исследование на модели при достаточно высоких давлениях  Па. Такая замена усложняется еще и тем, что теплофизические параметры существенно изменяются с изменением температуры. Это требует коррекции системы дифференциальных уравнений состоящей например в том, что переменные величины нельзя выносить из под знака производной. Основную систему дифференциальных уравнений необходимо дополнить уравнениями, описывающими изменение физических параметров в зависимости от температуры