
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Численные методы
Лабораторная работа № 6 «Приближение функций»
Вариант № 3
Задача: 6.22.1
Выполнила студентка группы А-14-02
Захарова Юлия
2004
Задание:
Дана функция ![]() . Приблизить функцию интерполяционным
многочленом Ньютона, причем степень многочлена подобрать таким образом, чтобы max величина погрешности не превышала заданной величины
. Приблизить функцию интерполяционным
многочленом Ньютона, причем степень многочлена подобрать таким образом, чтобы max величина погрешности не превышала заданной величины ![]()
Теория:
Если функция ![]() задана таблично,
причем с постоянным шагом h, то для ее интерполяции
можно использовать интерполяционный многочлен Ньютона, имеющий вид
задана таблично,
причем с постоянным шагом h, то для ее интерполяции
можно использовать интерполяционный многочлен Ньютона, имеющий вид 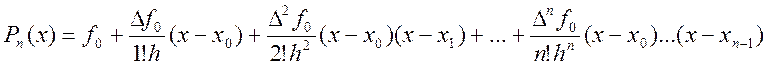
В нашем случае степень многочлена неизвестна, ее нужно подобрать, исходя из заданных условий, для чего предлагается следующий алгоритм:
Задать степени интерполяционного многочлена n некоторое значение.
Поскольку многочлен степени n
определяется n+1 точкой, то вычислить сетку с шагом 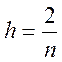
![]()
Далее необходимо найти ![]() по
отрезку [-1,1]. Но невозможно искать разность
по
отрезку [-1,1]. Но невозможно искать разность ![]() в
каждой точке отрезка, значит, надо ограничиться разностью в узлах сетки.
Но опять же, поскольку мы используем для интерполяции многочлен Ньютона, то в
узлах сетки данная разность попросту равна 0. Как вариант, можно отойти от узла
на
в
каждой точке отрезка, значит, надо ограничиться разностью в узлах сетки.
Но опять же, поскольку мы используем для интерполяции многочлен Ньютона, то в
узлах сетки данная разность попросту равна 0. Как вариант, можно отойти от узла
на ![]() , высчитать там значение
вышеприведенной разности и принять его за
, высчитать там значение
вышеприведенной разности и принять его за ![]() .
Среди всех разностей найти максимум и, если он удовлетворяет заданным условиям,
принять данное n за искомую степень. Если же нет, то
увеличить n на 1 и повторить все действия.
.
Среди всех разностей найти максимум и, если он удовлетворяет заданным условиям,
принять данное n за искомую степень. Если же нет, то
увеличить n на 1 и повторить все действия.
Также надо отметить, что, сдвигаясь от последнего узла на некий шаг, мы выходим за пределы отрезка [-1,1] , тем самым переходя к решению задачи об экстраполировании, при этом погрешность резко возрастает. В данном случае целесообразно отказаться от рассмотрения погрешности в последней «сдвинутой» точке и ограничиться лишь предыдущими.
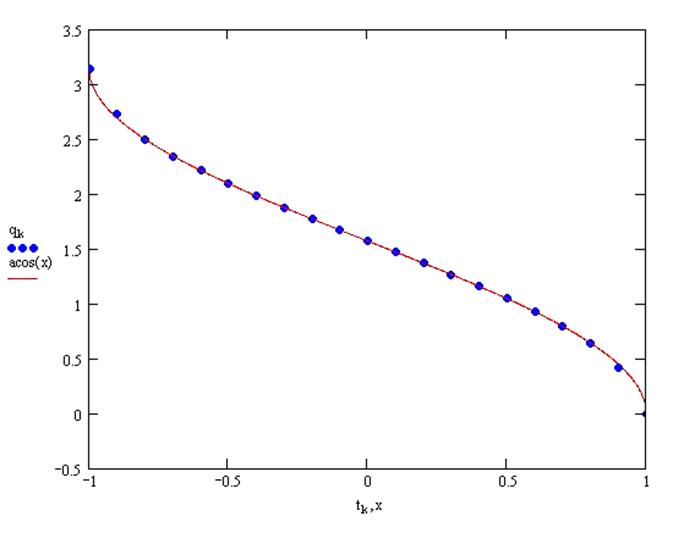
Ответ: степень интерполяционного многочлена, при котором максимальная разность не превышает 0.001 равна 11.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.