Ознакомление с системой «ЭВРИСТА», изучение способов моделирования временных рядов, методов их визуального анализа и редактирования

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Лабораторные работы № 1-3

по курсу анализ стохастических процессов

Выполнили
Студенты	Куликова А.В. Родин Д.В.
Группа	А – 01 – 03
Дата	18.10.07

Принял
Преподаватель
Дата

Цель работы

Ознакомление с системой «ЭВРИСТА», изучение способов моделирования временных рядов, методов их визуального анализа и редактирования. Изучение методов предварительной обработки экспе­риментальных данных.

Программа исследований

Часть 1

1.  Используя методическое описание системы «Эвриста» и системную помощь, ознакомиться с методами обработки временных рядов, представленными в пакете, возможностями пакета по моделированию, хранению, табличному и графическому представлению временных рядов, назначением пунктов главного меню и функциональных клавиш.

2.  Смоделировать временной ряд, заданный моделью авторегрессии-скользящего среднего АРСС(1,1).

3.  Используя интерпретатор формул, смоделировать  временные ряды, заданные формулами.

4.  Для любого из pядов X или Y провести визуальный анализ ано­мальных измерений.

5.  Отредактировать выбранный в п.4 временной ряд.

6.  Сохранить отредактированные экспериментальные данные.

Часть 2

1.  Провести визуальный анализ всех исходных временных  рядов и их сглаженных изображений. Сглаживание провести методом простого сколь­зящего среднего с разным числом точек усреднения. Сделать выводы о предполагаемом составе рядов и качестве оценивания тренда при разном количестве точек усреднения.

2.  Проверить гипотезу о случайности наблюдений в рядах данных, ис­пользуя критерии инверсий, серий и поворотных точек для всех рядов. Сделать вывод о независимости наблюдений в исследуемой реализа­ции и о возможном альтернативном предположении, если гипотеза о слу­чайности отвергнута.

3.  Исследовать стационарность рядов, возможно включающих тренд, используя: анализ ряда оценок математического ожидания и дисперсии и критерии проверки случайности; анализ оценки автокорреляционной функции (АКФ) и спектральной плотности мощности (СПМ).

4.  Провести  выделение и удаление тренда методом простого сколь­зящего среднего (в тех рядах, где он обнаружен), используя подходящее число точек сглаживания для каждого ряда.

5.  Провести повторный анализ свойств рядов с удаленным трендом различными способами: визуально, с помощью подходящего критерия случайности, с помощью оценок СПМ и АКФ.

6.  По результатам п.п. 2, 3, 4  и 5  сделать вывод о свойствах времен­ных рядов  и их предполагаемых моделях (возможных компонентах ряда).

7.  Провести начальный статистический анализ рядов с удаленным трендом, рассчитав оценки основных числовых характеристик, проверив гипотезу о нормальности и подобрав вид распределения, если гипотеза о нормальности отвергнута.

Часть 3

1.  Любым из известных способов проанализировать наличие тренда и колебательной составляющей в рядах.

2.  Для рядов, предположительно содержащих тренд, оценить порядок К>1 линейной полиномиальной регрессии, описывающей тренд.

3.  Оценить тренд, построив: полиномиальную регрессию выбранного порядка К, простую регрессию для линейной и экспоненциальной базисных функций.

4.  Для каждого из методов выделить тренд, построить графики и рас­печатать (выводить на один рисунок все оценки тренда, полученные раз­ными методами для одного ряда).

5.  Удалить обнаруженные и оцененные тренды из рядов, провести по­вторный анализ наличия тренда и качества удаления тренда разными спо­собами.

6.  Провести разделение временного ряда на компоненты, используя цифровую фильтрацию.

Исходные данные для проведения исследований

Часть 1

Параметры АРСС модели: АР = 0.4; CC = 0.5

Х = 0.3*SIN(0.05*2*PI*CASE(300)) + 0.7*NOISE(300)

Y = 0.08*LOG(0.2*CASE(300)) + NOISE(300) + ar1

Часть 2

E005 = EXP(0.005*CASE(500)) + 2*NOISE(500)

SI002 = SIN(0.002*2*pi*CASE(500)) + NOISE(500)

SI001 = 5*SIN(0.0001*2*pi*CASE(500)) + 0.5*NOISE(500) + A,
где A = SIN(0.01*2*pi*CASE(500)).

Часть 3

E005® EXP(0.005*CASE(500)+2*NOISE(500)

SI0001®5*SIN(0.0001*2*pi*CASE(500))+B+NOISE(500),

B ® SIN(0.2*2*pi*CASE(500))+2

Результаты исследований

Часть 1.

Проводится визуальный анализ временного ряда X, представляющего собой сильно зашумленные данные. График выбранного ряда имеет вид:

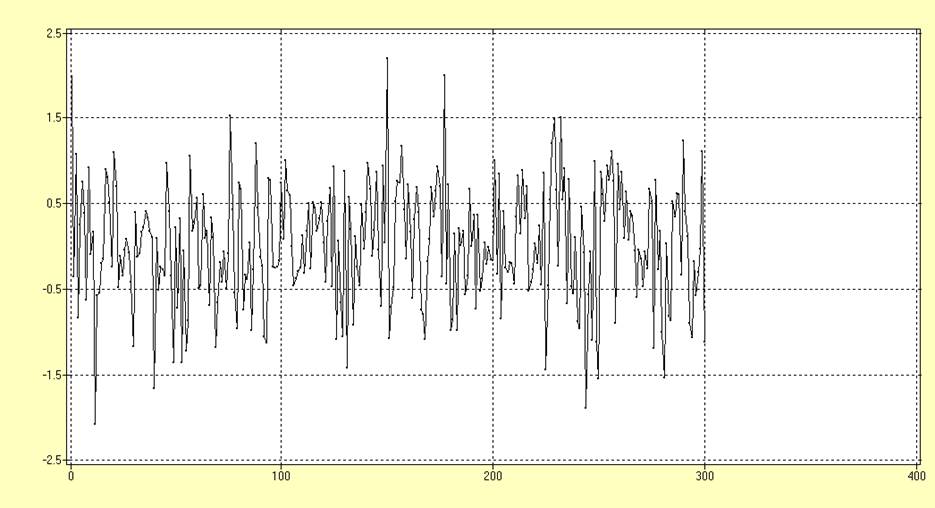
В результате проведения визуального анализа аномальных измерений были обнаружены следующие 2 выделяющиеся точки, которые могли бы быть обусловлены влиянием импульсной помехи:

	минимум	максимум
значение	-2.0798	2.1956
индекс	12	150

Графики частей ряда, содержащих выделяющиеся наблюдения, имеют вид:

минимальное значение	максимальное значение

График самой насыщенной части ряда имеет вид:

 

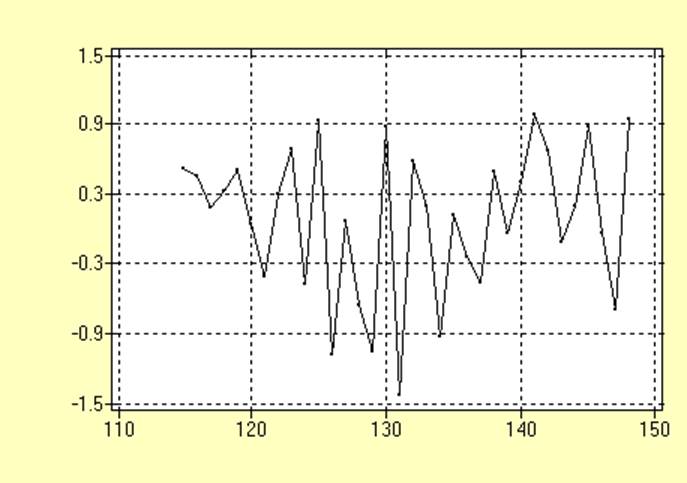
После проведения аппроксимации исходного временного ряда полиномом первого порядка получены следующие данные:

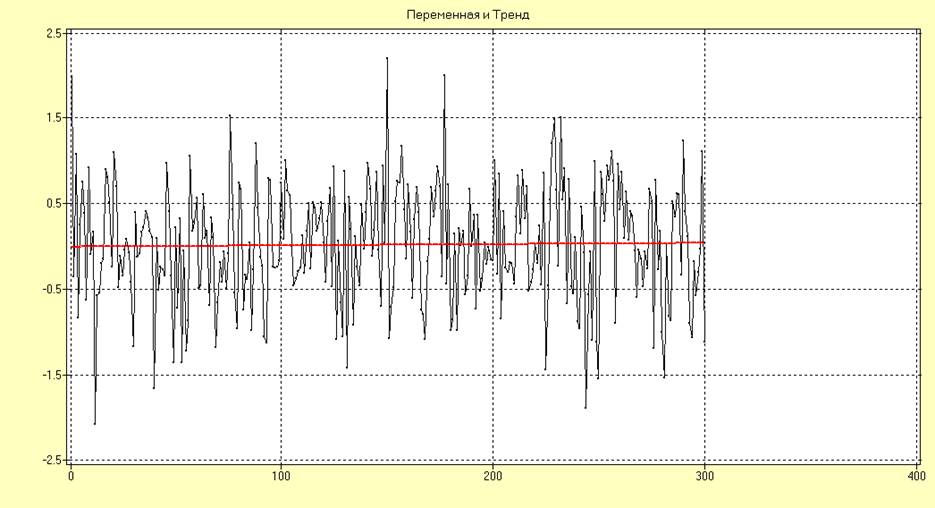
Анализируя график, можно заметить, что в исходном временном ряде прослеживается тенденция к незначительному увеличению значений.

Значения найденных выделяющихся точек можно заменить значениями, полученными линейной интерполяцией соседних измерений:

	минимум	максимум
индекс	12	150
измерение	-2,0798	2,1956
соседние измерения	0,1671	0,0393
	-0,5759	-1,0742
новое значение	-0.2044	-0,5175

Графики частей ряда, содержавших выделяющиеся наблюдения, после замены принимают вид:

минимальное значение	максимальное значение

Значения найденных выделяющихся точек можно заменить соответствующими значениями из аппроксимирующей полиномиальной зависимости:

	минимум	максимум
индекс	12	150
измерение	-2,0798	2,1956
новое значение	-0.0043	0.0162

Графики частей ряда, содержавших выделяющиеся наблюдения, после замены принимают вид: