Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ .
Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.
Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.
Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.
Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.
Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.
а)
б)
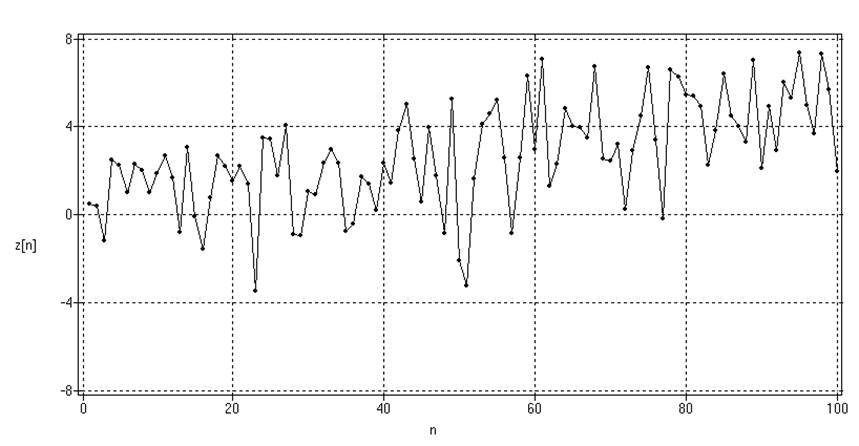
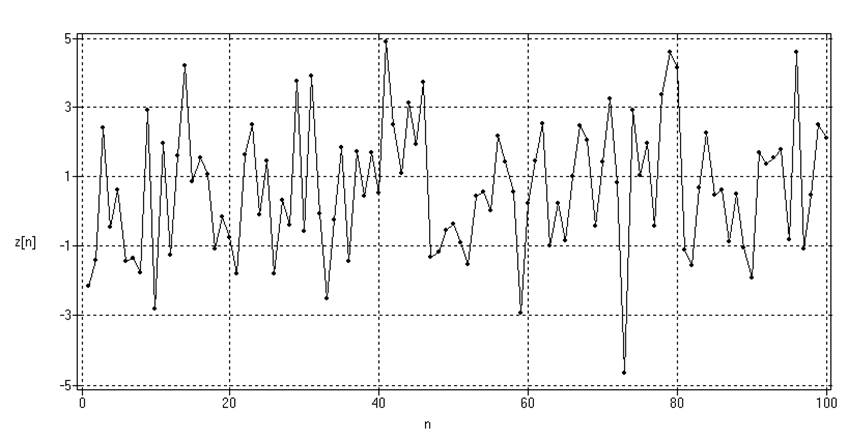
Рис.13. Временные ряды с
явным (а) и неявным (б) трендами
а) автокорреляционная последовательность временного ряда
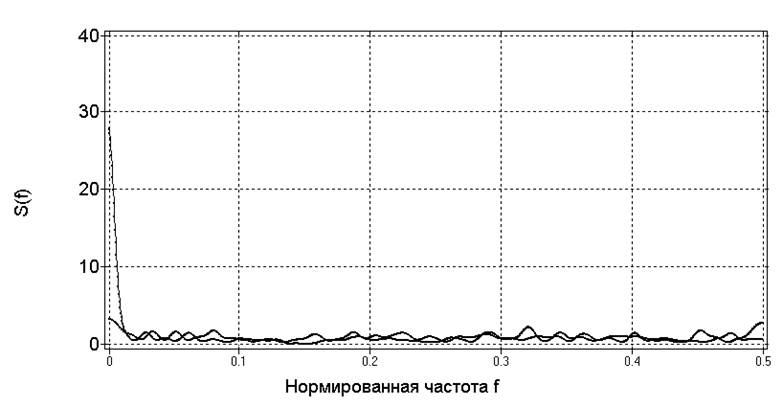
б) спектральная плотность
мощности
Рис.15. Характеристики
временных рядов до и после удаления тренда
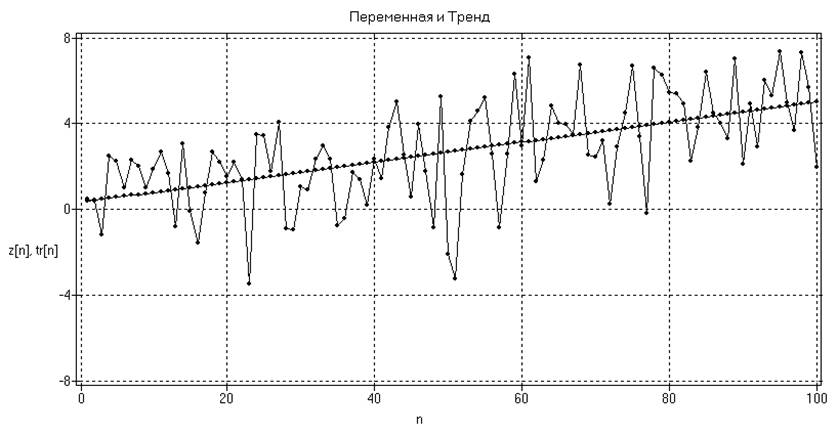
а)
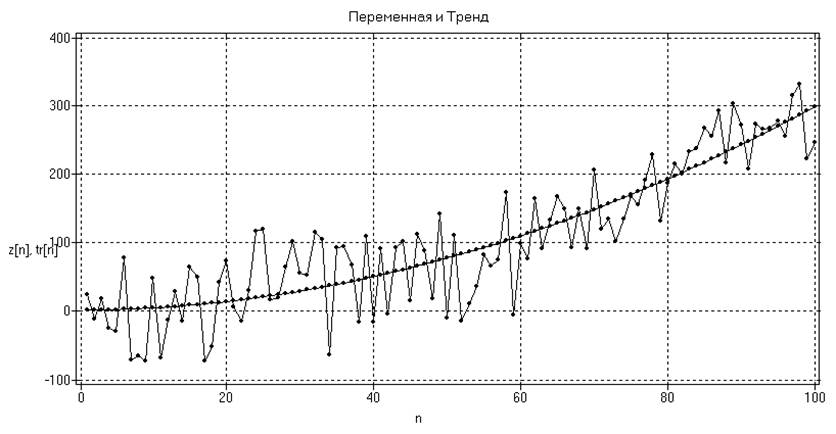
б)
Рис.16. Аппроксимация
тренда полиномами первого (а) и второго (б) порядков
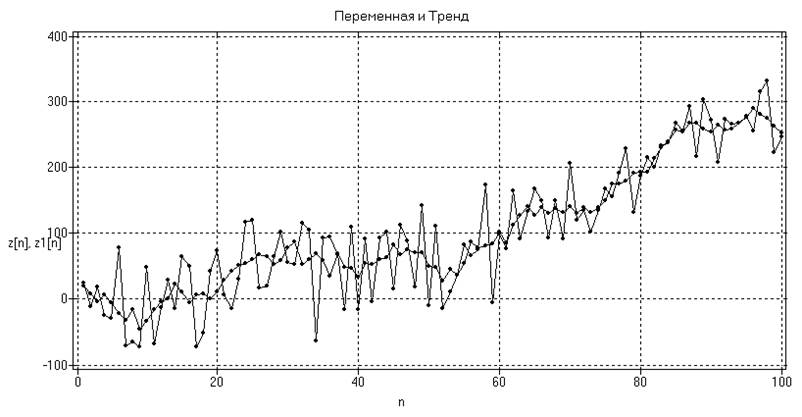
а)
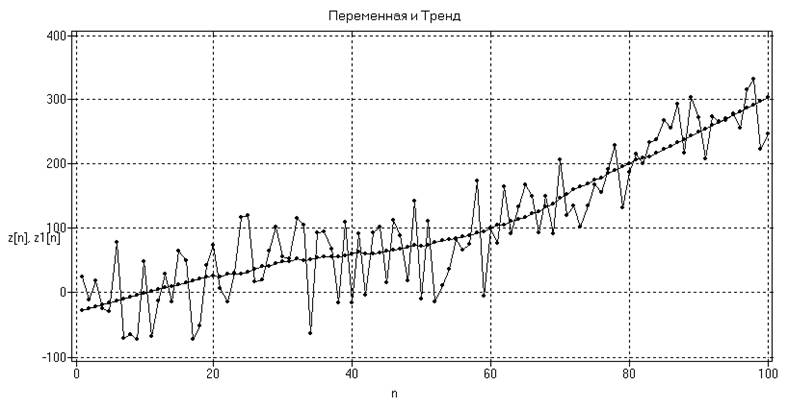
б)
Рис. 17. Результат сглаживания z1( t) временного ряда z( t) методом простого
скользящего среднего при m=5 (a)
и m=55 (б)
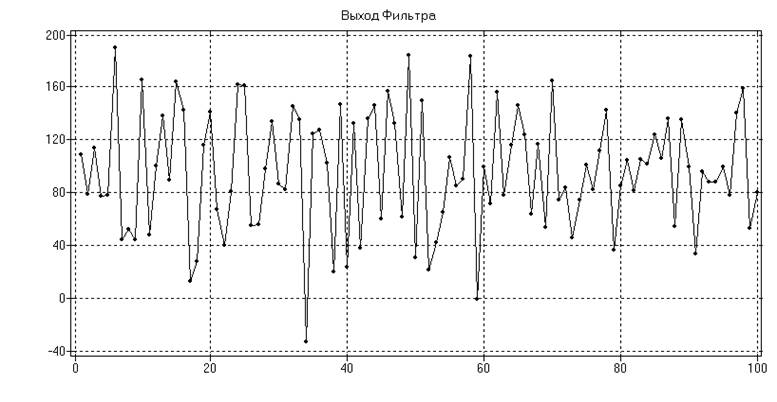
а)
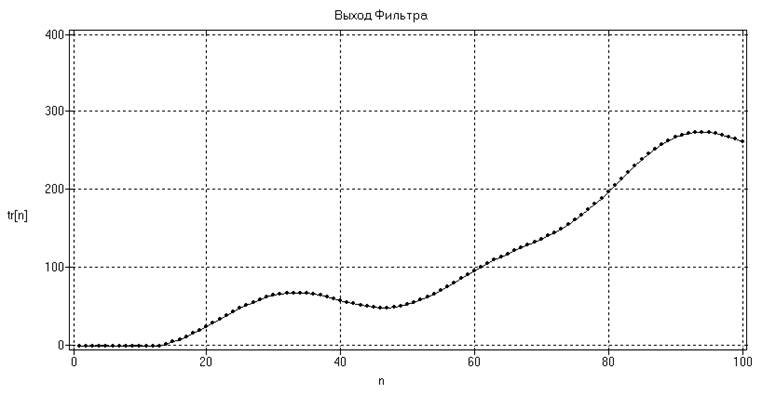
б)
Рис.
18. Результат фильтрации временного ряда:
а) высокочастотная фильтрация, б) низкочастотная
фильтрация.
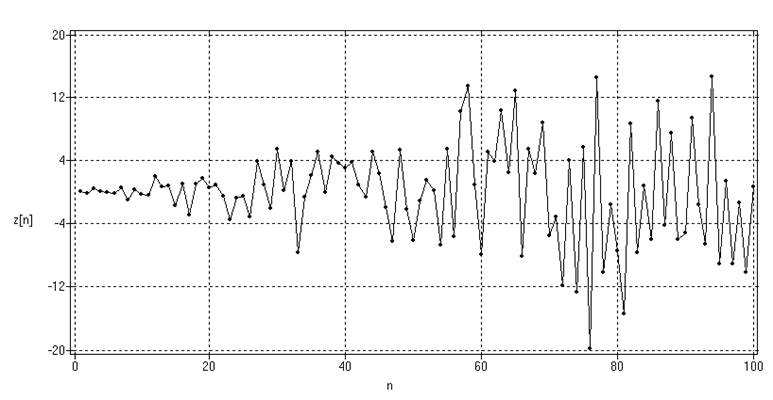
а)
б)
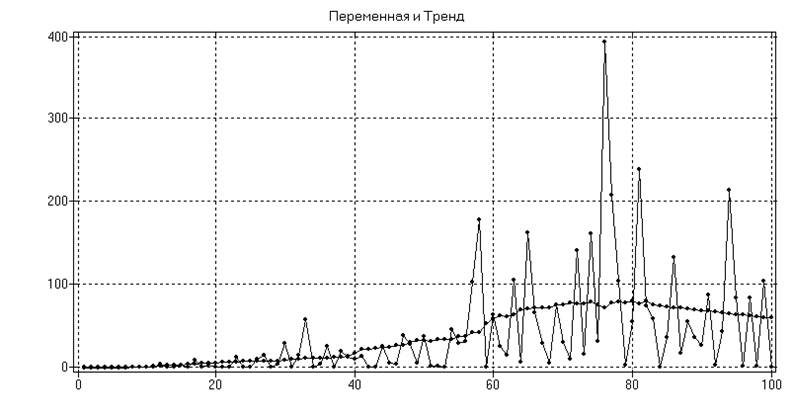
Рис.19. Нестационарный по дисперсии ряд (а) и сглаживание
квадратов центрированных ординат ряда (б)
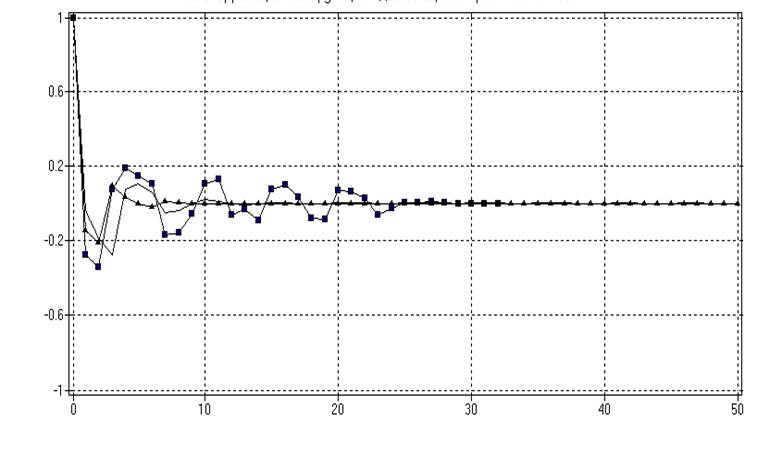
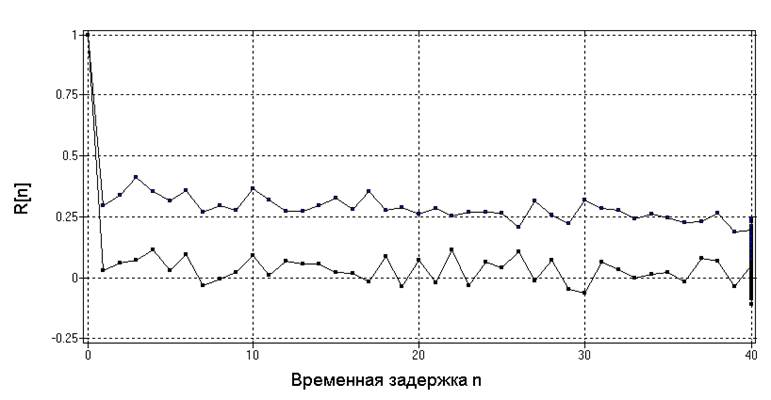
Рис. 20.
Автокорреляционная функция процесса и две ее оценки для реализаций длины N1=100
и N2=500
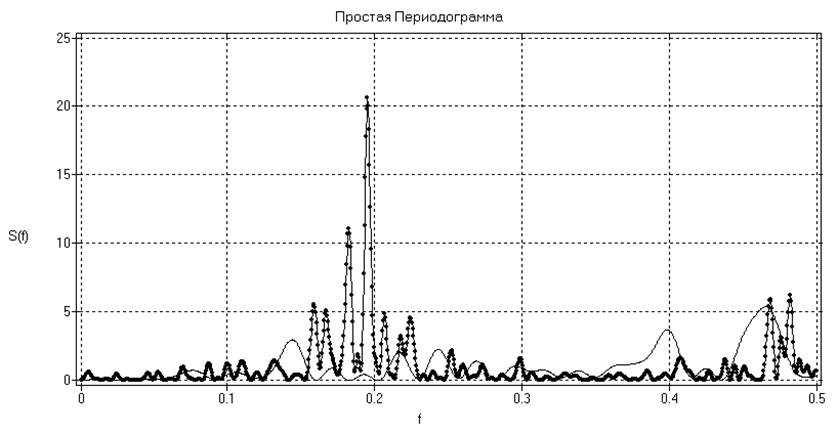
Рис. 21. Простые
периодограммы при длинах реализаций N=50 и N=500
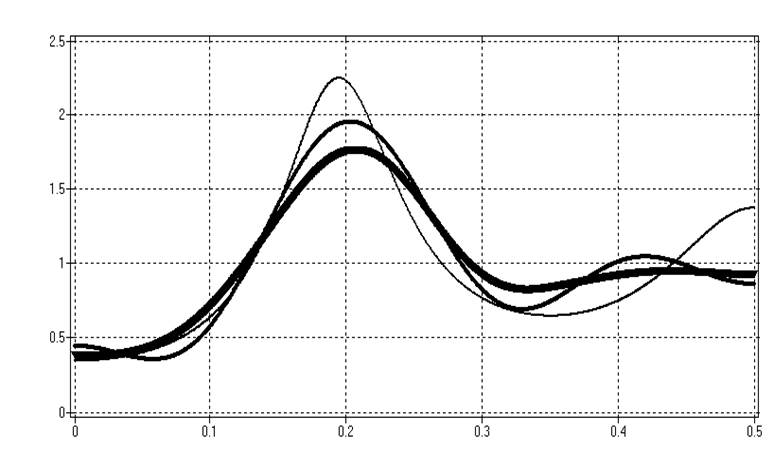
а)
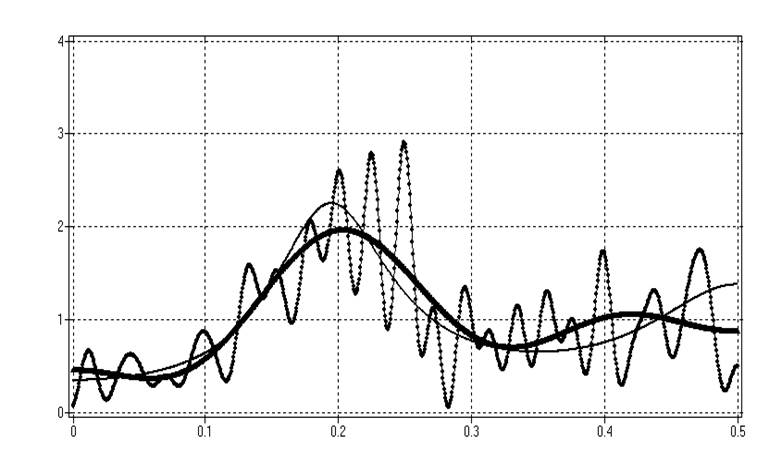
б)
Рис.24. а) СПМ
и две сглаженные оценки, полученные с использованием окон: прямоугольного и
Хемминга при адаптивном выборе ширины окна
б) СПМ и две оценки с использованием прямоугольного окна ширины
M=5 ( сильное сглаживание) и M=50
(слабое сглаживание)
Дисперсия шума
=1.00 (Дисперсия шума)/(Дисперсия ряда) =0.642
АР-Порядок Статистики
Парзен
3 -1.538855
Акаике
(инф) 3 -0.427002
Акаике
(ср.знач.) 3 0.652462
Хэннан-Куин
3 -0.432040
Критерии
порядка АРCC - модели
АР-Порядок
CC-Порядок Статистика
3
0 20.3904
Параметр Оценка Станд.Ошибка
T-Значение P-Значение
АР(1) = 0.141966 0.035728
3.973525 4.06523 e-05
АР(2) = 0.186698 0.035314
5.286782 9.33950 e-08
АР(3) = 0.601460 0.035728
16.834427 0
Сумма кв. Остатков =468.1387714
Хи-Квадрат Тест автокорреляции Остатков =12.249 с
числом степеней свободы=19
Остатки есть Белый Шум с вероятностью не более чем
=0.87466
а)
Дисперсия
АР-шума =5.350 (Дисперсия шума)/(Дисперсия ряда) =0.959
АР-Порядок
Статистики
Парзен
8 -1.007534
Акаике
(инф) 8 -0.005472
Акаике
(ср.знач.) 8 0.994545
Хэннан-Куин
8 -0.012242
Критерии
порядка АРCC - модели
АР-Порядок
CC - Порядок Статистика
2
1 853.3704481
Оценка параметров
модели АР(8)
Параметр Оценка Стандартная ошибка
T-Значение P-Значение
АР(1) = 0.00531 0.04440
0.119599 0.45242
АР(2) = 0.00454 0.044346
0.10246 0.45921
АР(3) = 0.07504 0.044343 1.69232
0.04560
АР(4) = -0.0350 0.044218
0.79155 0.21450
АР(5) = -0.1057 0.044218
2.39196 0.00856
АР(6) = -0.0050 0.044343
0.11496 0.45425
АР(7) = 0.05122 0.044344
1.15510 0.12430
АР(8) = 0.11919 0.044402
2.68434 0.00375
Сумма кв. Остатков =2636.952
Хи-Квадрат Тест автокорреляции Остатков =8.972 с
числом степ. свободы = 14
Остатки есть Белый Шум с вероятностью не более чем
=0.832782
Оценка параметров
модели АР(3)
Параметр Оценка Стандартная ошибка
T-Значение P-Значение
АР(1) = -0.00202 0.04452428245
0.04550 0.481863
АР(2) = 0.022831 0.0445126649
0.51293 0.304113
АР(3) = 0.093777 0.04452428245
2.10620 0.017843
Сумма кв. Остатков =2754.269862
Хи-Квадрат Тест автокорреляции Остатков =20.723 с
числом степеней свободы = 19
Остатки
есть Белый Шум с вероятностью не более чем =0.352257
б)
Рис.
25. Оценивание порядка и параметров модели временного ряда, заданного как АР(3)
с параметрами а(1)=0,1 а(2)=0,2 а(3)=0,6;
а) при отсутствии помех ; б) при
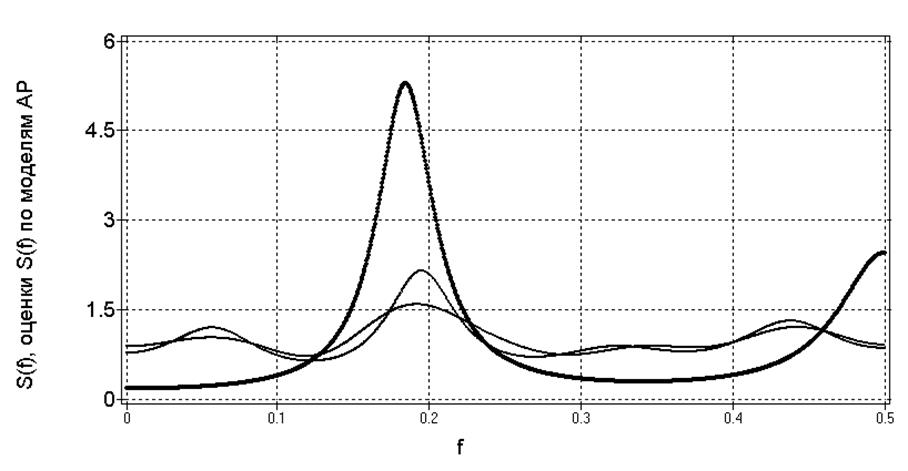
помехе e типа «белый» шум с дисперсией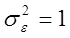
а)
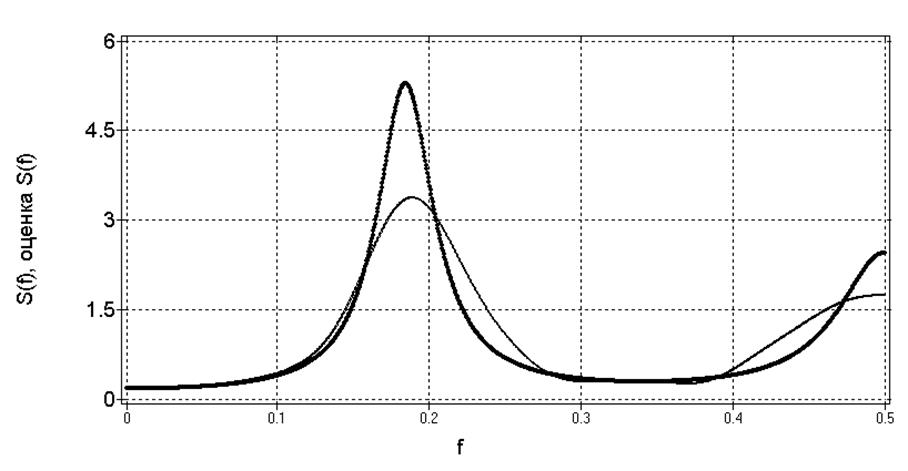
б)
Рис. 26. Теоретическая функция СПМ
временного ряда и ее оценки по моделям типа АР.
а) при отсутствии помехи измерения и
использовании модели АР(3);
б) при измерении с помехой и
использовании моделей АР(3) и АР(8).
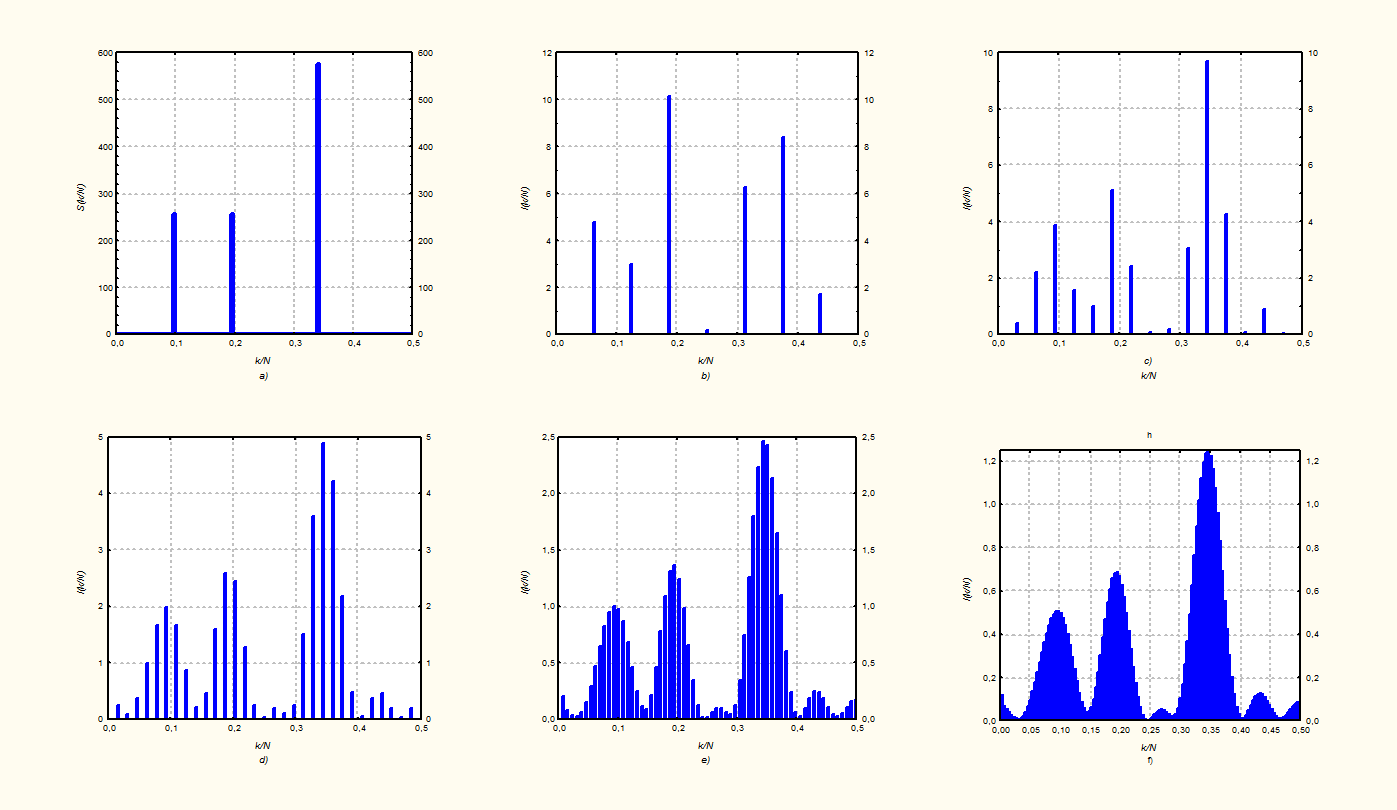
Рис. 28. Влияние процедуры дополнения нулями: а) –
теоретическая спектральная плотность; b ) – периодограмма по 16 наблюдениям (N
=16 ); с) – d ) – то же, но с дополнительными нулями ( с) – N 0 = 16; d )
– N 0 =
48; e ) – N 0 =112; f ) – N 0 = 240)
Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ .
Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.
Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.
Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.
Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.
Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.
.
