Выполнили |
Бригада №2 |
Студенты |
Козлов М. А. Попов И. О. |
|
Группа |
А – 01 – 03 |
|
Дата |
16.11.07 |
Принял |
|
Преподаватель |
|
Дата |
Цель работы
Изучение непараметрических методов оценивания спектральной плотности мощности (СПМ) временного ряда и свойств цифровых оценок.
Программа исследований
2. Исследовать свойства оценки СПМ в виде простой периодограммы, рассчитанной по реализациям различной длины N1, N2 и N3 для всех типов процессов. Сделать выводы об изменении точности оценки в зависимости от длины реализации во всех случаях. Оценки для "белого" шума и процесса Х2 вывести на печать (для процесса Х2 - три графика на один рисунок).
3. Исследовать свойства оценки СПМ в виде усредненной периодограммы для различных длин сегментов (10, 50 и 100 интервалов дискретизации) при длине N3 реализаций:
· процесса типа "белый" шум с интенсивностью N0 = 1.0,
· ряда Х3.
Сделать вывод о влиянии параметра усреднения (длины сегмента) на оценку спектальной плотности. Для расчетов оценки использовать прямоугольное «окно», ширина которого определяет длину сегмента и устанавливается вручную. Оценки СПМ для процесса Х3 вывести на один график.
· процесса типа "белый" шум с интенсивностью N0 = 1.0,
· ряда Х2.
Сделать вывод о влиянии ширины и типа "окна" на оценку спектра. Для исследования использовать "окна": Бартлетта и Ханна(Хэннинг) различной ширины (10, 50 и 100 интервалов дискретизации). Вывести на печать графики оценок СПМ процесса Х2 для двух разных окон одинаковой ширины и для одного типа окна при различной его ширине.
Исходные данные для проведения исследований
· типа "белый" шум с интенсивностью N0 = 1.0,
· X1 = SIN(0.05*2*PI*CASE(n)),
· X2 = SIN(0.05*2*PI*CASE(n)) + 2*NOISE(n),
· X3 = SIN(0.1*2*PI*CASE(n)) + Х2.
Результаты исследований
Исследование свойств оценки СПМ в виде простой периодограммы.
Оценки СПМ в виде простой периодограммы, рассчитанной по реализациям различной длины N1, N2 и N3 для процесса типа белый шум имеют вид:
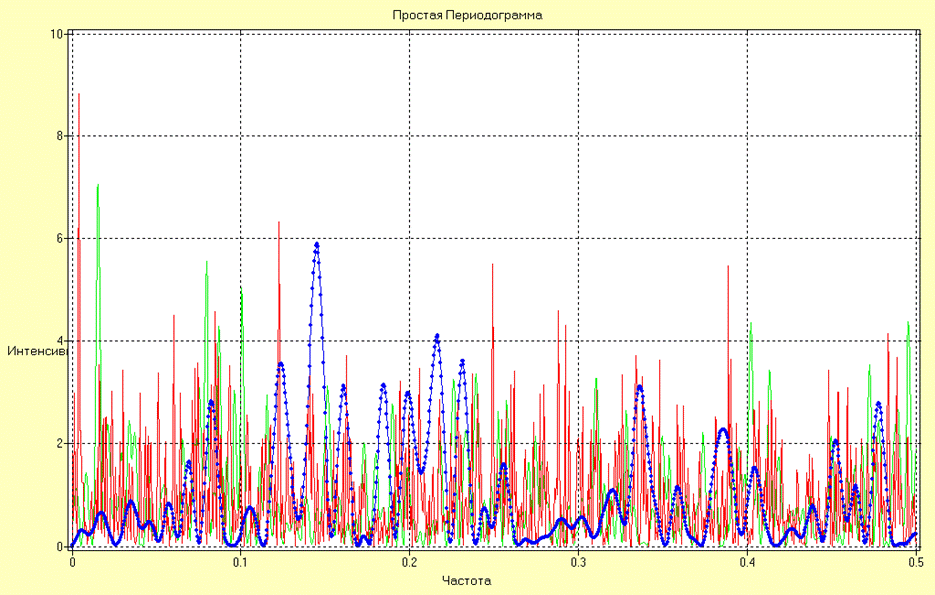
Из представленных результатов видно, что с увеличением длины выборки разрешающая способность оценки СПМ увеличивается и оценка становится менее сглаженной. Данная оценка обладает большой дисперсией и является несостоятельной, поэтому судить по ней о частотном составе процесса затруднительно.
Оценки СПМ в виде простой периодограммы, рассчитанной по реализациям различной длины N1, N2 и N3 для процесса Х1 имеют вид:
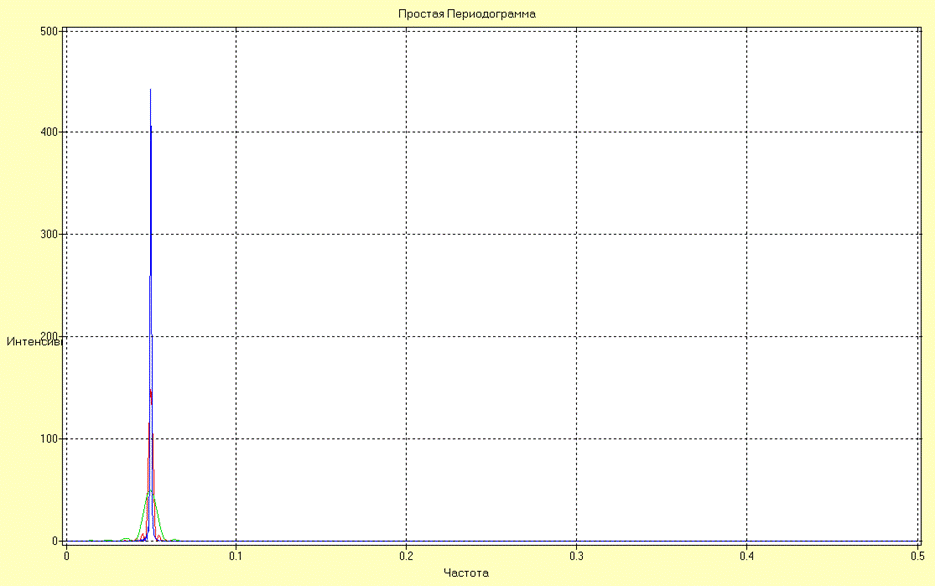
Анализируя полученные результаты можно сделать вывод об увеличении точности оценивания частоты спектрального пика с ростом длины реализации за счет увеличения разрешающей способности.
Оценки СПМ в виде простой периодограммы, рассчитанной по реализациям различной длины N1, N2 и N3 для процесса Х2 имеют вид:
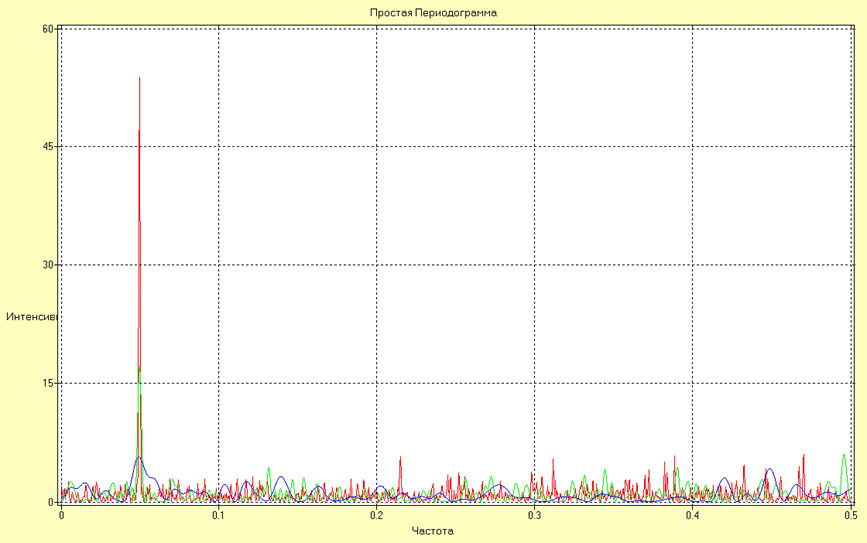
Анализируя полученные результаты можно сделать вывод о росте качества оценивания частоты спектрального пика с увеличением длины реализации за счет увеличения разрешающей способности (уменьшается размывание).
Оценки СПМ в виде простой периодограммы, рассчитанной по реализациям различной длины N1, N2 и N3 для процесса Х2 имеют вид:
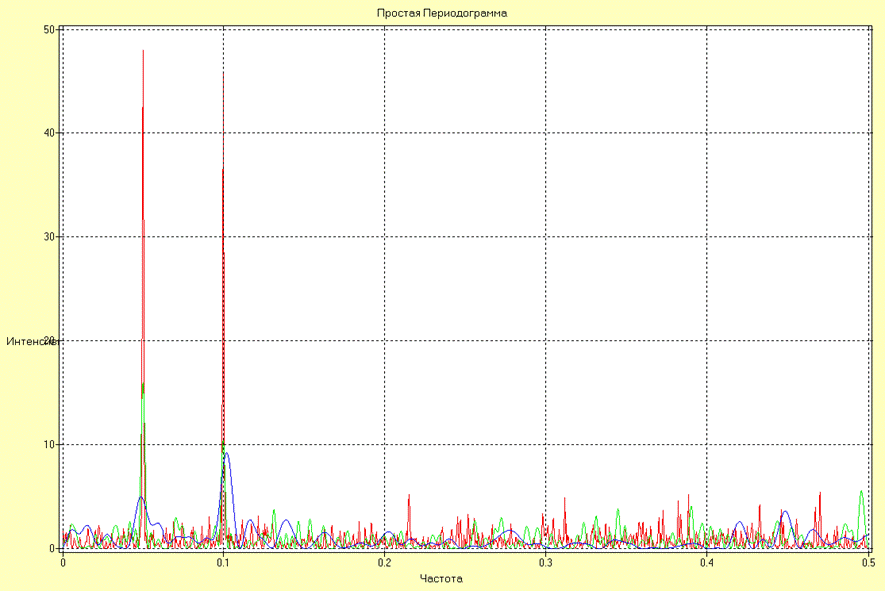
Анализируя полученные результаты можно сделать вывод о росте качества оценивания частот спектральных пиков с увеличением длины реализации за счет увеличения разрешающей способности.
Исследование свойств оценки СПМ в виде усредненной периодограммы для различных длин сегментов.
Оценки СПМ в виде усредненной периодограммы для различных длин сегментов (10, 50 и 100 интервалов дискретизации) при длине реализаций N3 = 1000 для процесса типа «белый» шум имеют вид:
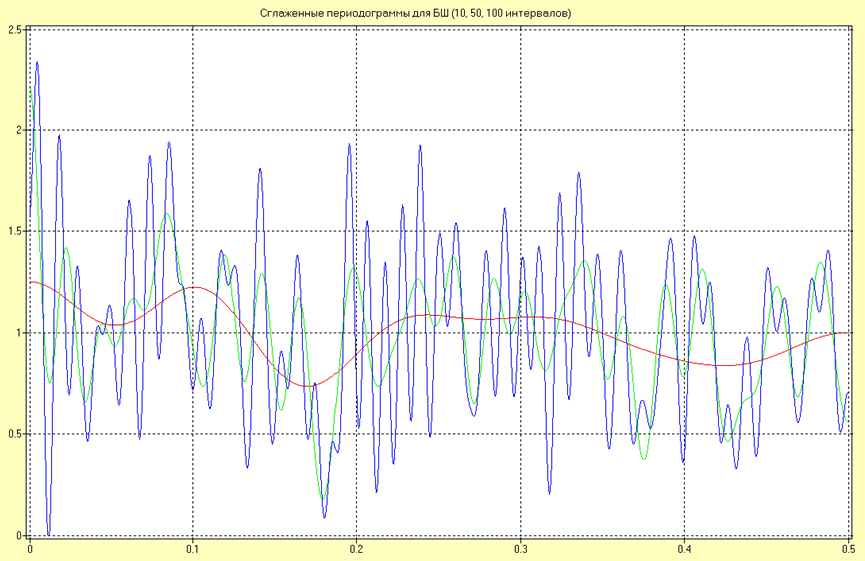
Анализируя полученные результаты можно сделать вывод об уменьшении точности оценивания и увеличении разрешающей способности с ростом количества интервалов дискретизации (увеличением ширины окна).
Оценки СПМ в виде усредненной периодограммы для различных длин сегментов (10, 50 и 100 интервалов дискретизации) при длине реализаций N3 = 1000 для процесса X3 имеют вид:
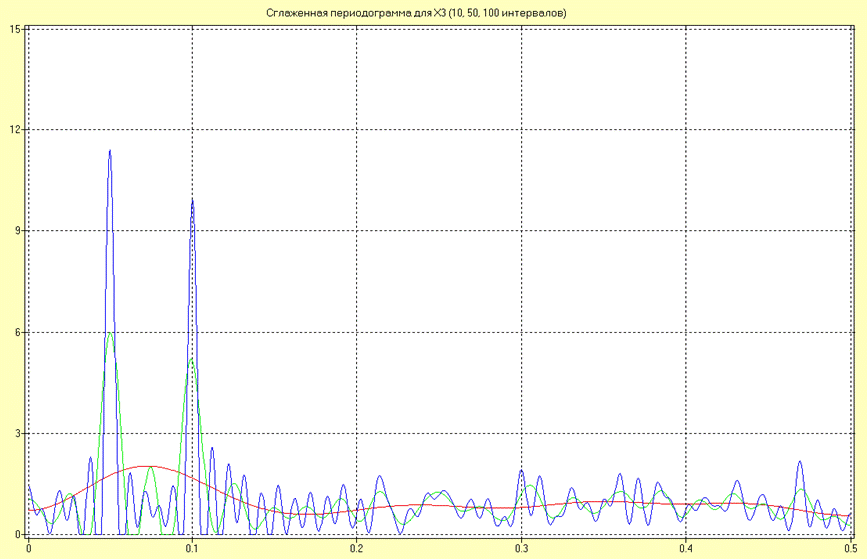
Анализируя полученные результаты можно сделать вывод о том, что с увеличением ширины окна разрешающая способность увеличивается и оценка становится все менее сглаженной, При этом спектральные пики, соответствующие основным гармоникам, становятся более выраженными. В то же время, при малой ширине окна качество оценивания мощности фоновой случайной помехи хуже, чем при большем значении.
Исследование свойств оценки СПМ в виде сглаженной периодограммы для различных типов «окон» при длине реализаций N3 = 1000.
Оценки СПМ в виде сглаженной периодограммы для окна Бартлетта для различных длин сегментов (10, 50 и 100 интервалов дискретизации) для процесса типа «белый» шум имеют вид:
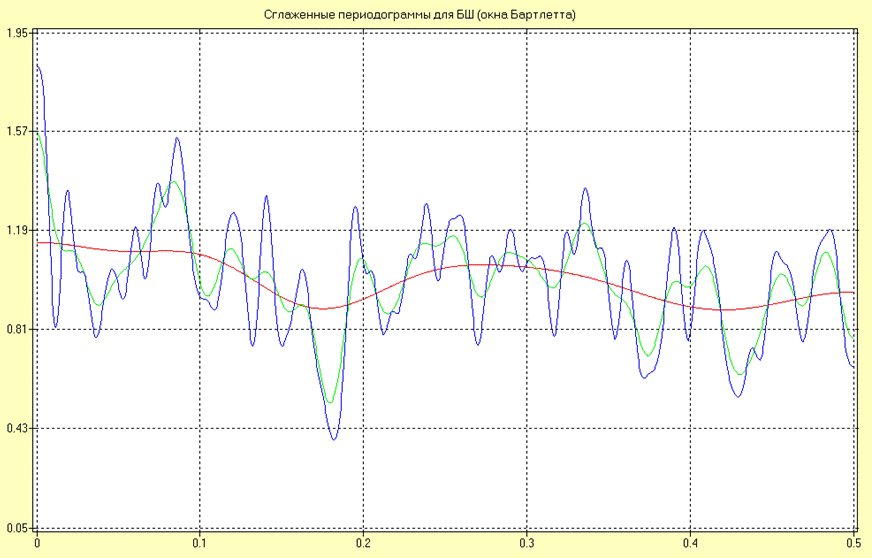
Анализируя полученные результаты можно сделать вывод об уменьшении точности оценивания и увеличении разрешающей способности с увеличением ширины окна.
Оценки СПМ в виде сглаженной периодограммы для окна Хэннинга для различных длин сегментов (10, 50 и 100 интервалов дискретизации) для процесса типа «белый» шум имеют вид:
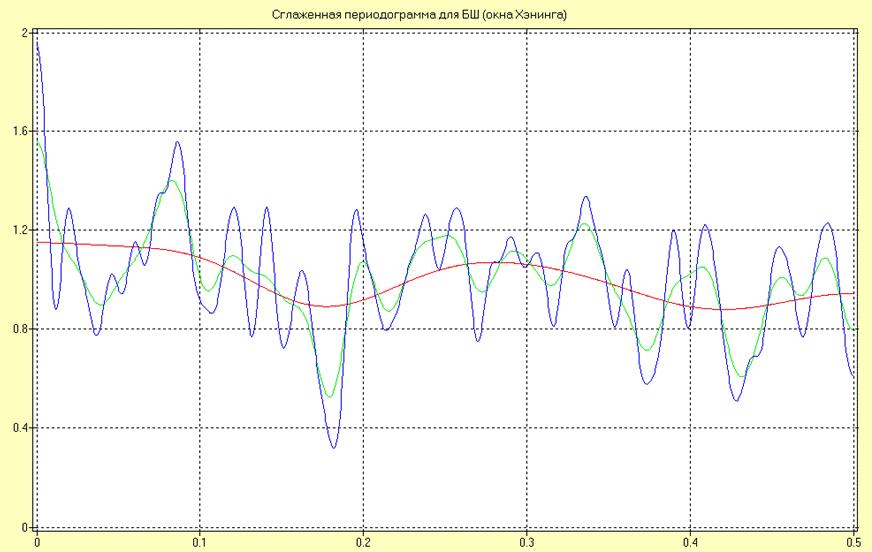
Анализируя полученные результаты можно сделать вывод об уменьшении точности оценивания и увеличении разрешающей способности с увеличением ширины окна.
Оценки СПМ в виде сглаженной периодограммы для окон Бартлетта и Хэннинга для 50 интервалов дискретизации для процесса типа «белый» шум имеют вид:
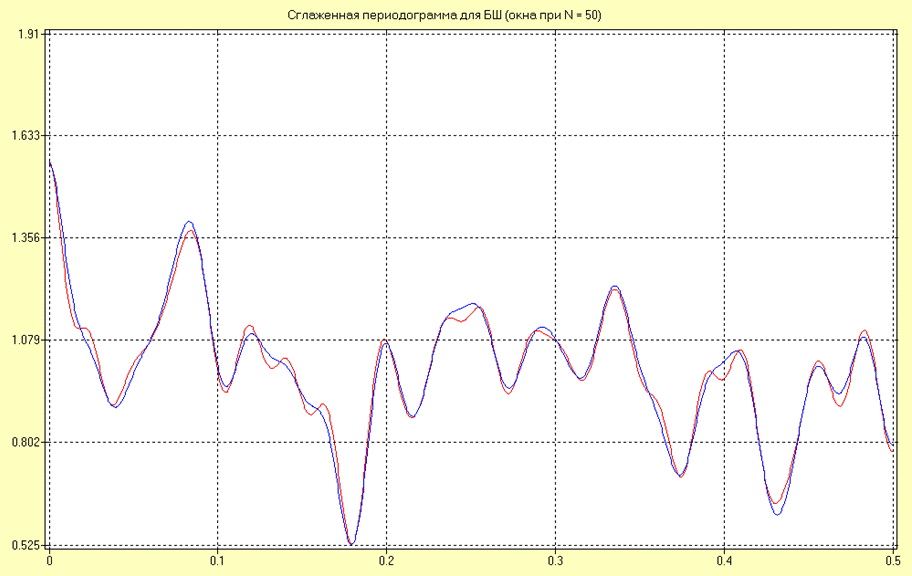
Исходя из анализа полученных результатов можно сделать вывод о том, что оценка, полученная с помощью окна Хеннинга является более сглаженной, что обусловлено меньшим влиянием эффекта наложения боковых лепестков.
Оценки СПМ в виде сглаженной периодограммы для окна Бартлетта для различных длин сегментов (10, 50 и 100 интервалов дискретизации) для процесса Х2 имеют вид:
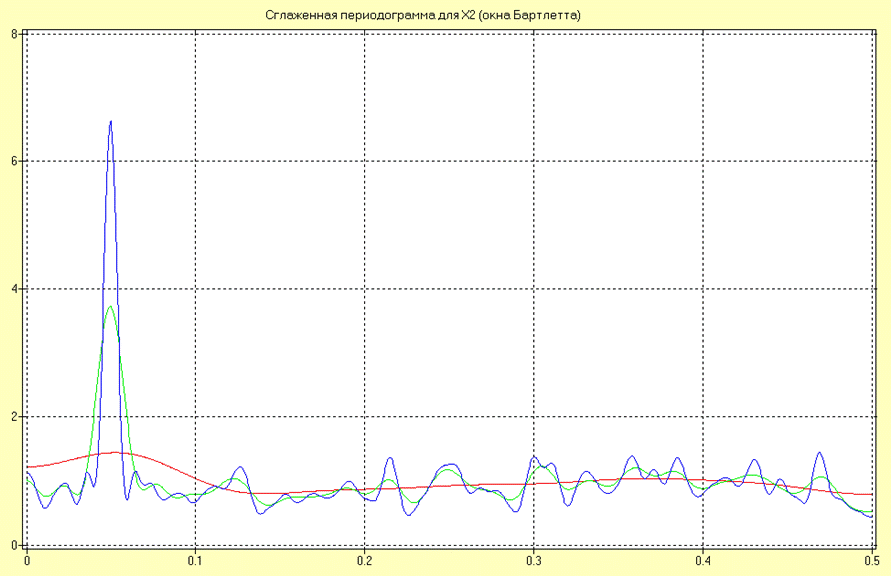
Анализируя полученные результаты можно сделать вывод о том, что с увеличением ширины окна разрешающая способность увеличивается и оценка становится все менее сглаженной, При этом спектральные пики, соответствующие основным гармоникам, становятся более выраженными. В то же время, при малой ширине окна качество оценивания мощности фоновой случайной помехи хуже, чем при большем значении. В данном случае наилучшим качеством обладает оценка, полученная при 50 интервалах дискретизации.
Оценки СПМ в виде сглаженной периодограммы для окна Хэннинга для различных длин сегментов (10, 50 и 100 интервалов дискретизации) для процесса Х2 имеют вид:
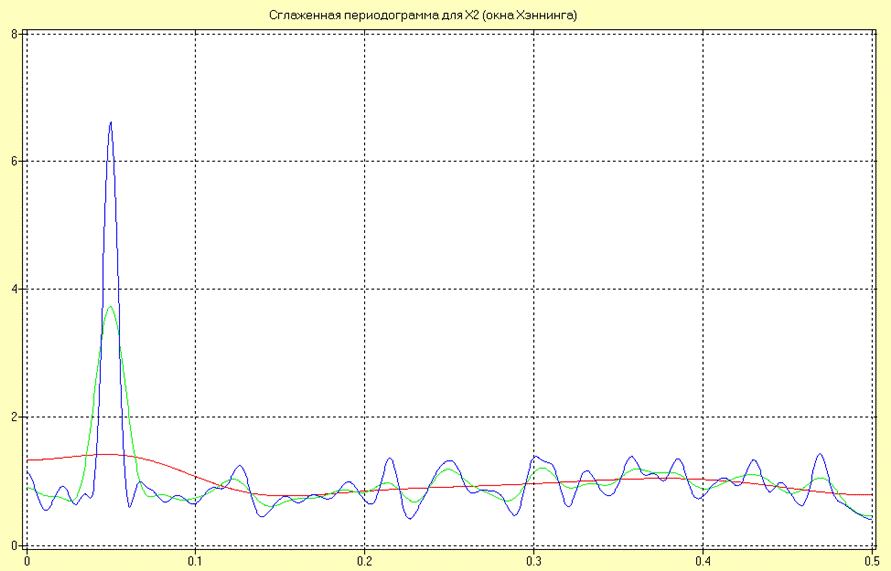
Из анализа полученных результатов следует вывод аналогичный сделанному при анализе результатов для окна Бартлетта.
Оценки СПМ в виде сглаженной периодограммы для окон Бартлетта и Хэннинга для 50 интервалов дискретизации для процесса Х2 имеют вид:
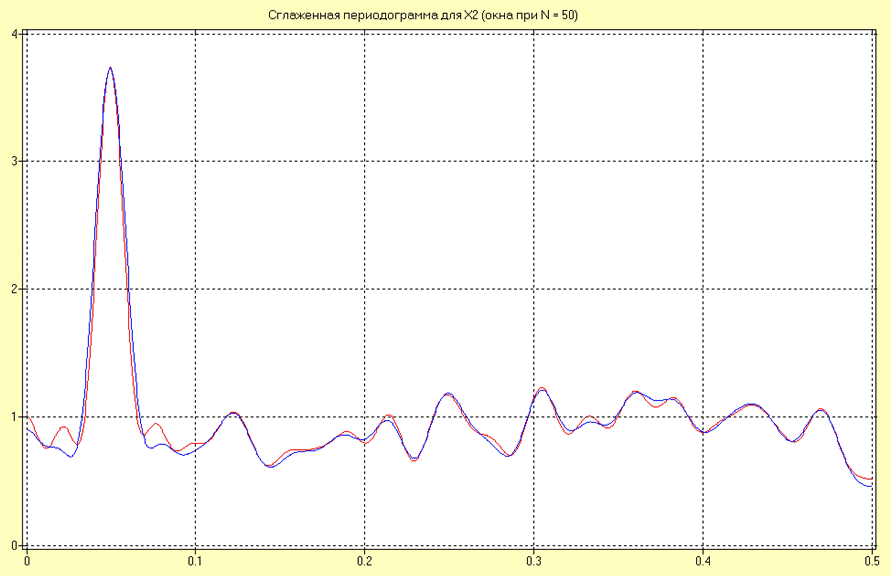
Исходя из анализа полученных результатов, можно сделать вывод о том, что оценка, полученная с помощью окна Хеннинга является более сглаженной, что обусловлено меньшим влиянием эффекта наложения боковых лепестков. Следовательно, вторая оценка является более точной.
Исследование ряда SI2
Оценка СПМ исследуемого ряда в виде простой периодограммы имеет вид:
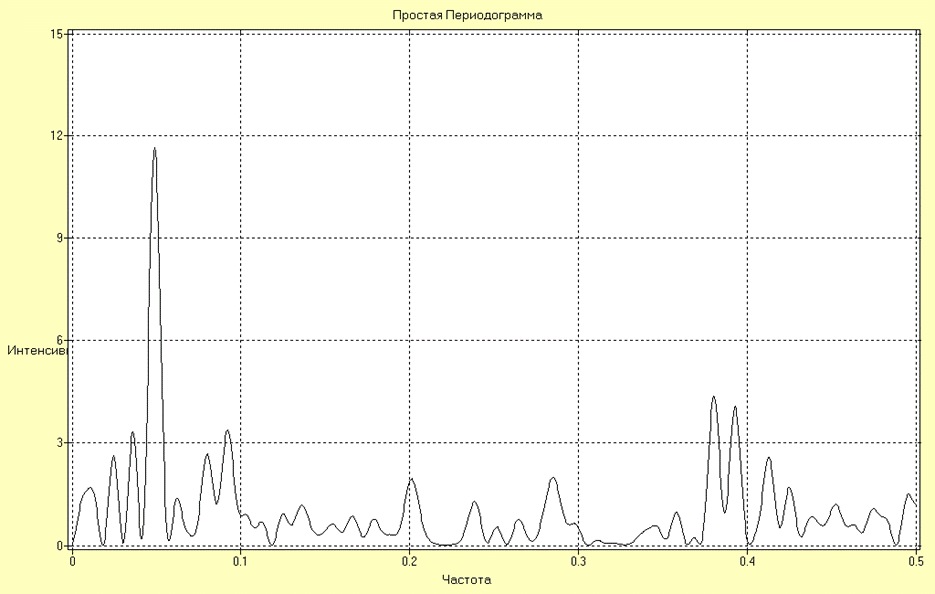
Данная оценка обладает наибольшей разрешающей способностью, однако точность оценивания незначительная и судить о спектральном составе ряда по ней затруднительно. Предварительно можно сделать вывод о наличии в составе ряда гармоник низкой частоты и высокой частоты. На средних частотах наблюдается провал.
Оценка СПМ исследуемого ряда в виде усредненной периодограммы имеет вид:
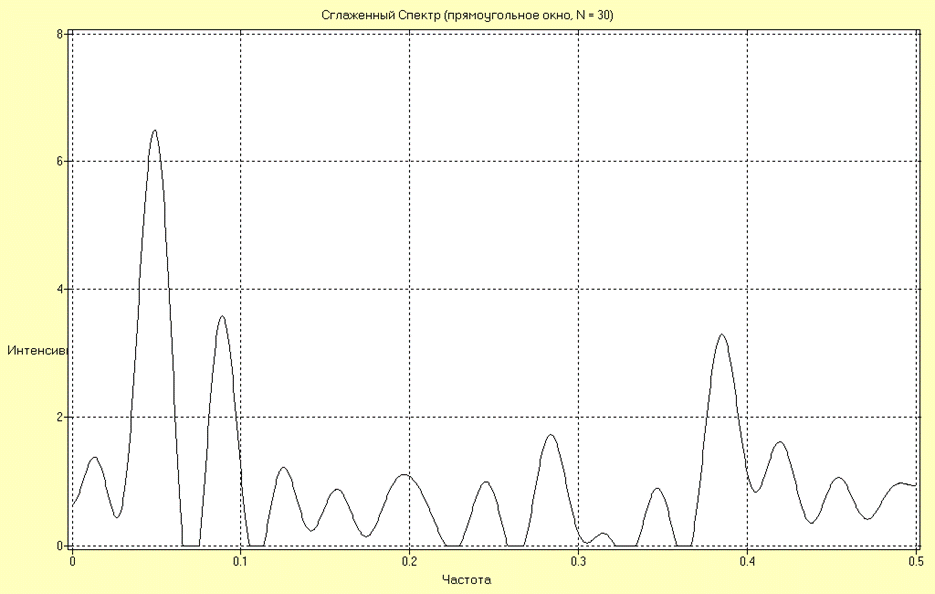
Точность данной оценки больше предыдущей. Анализ полученных результатов подтверждает сделанный вывод относительно спектрального состава ряда. Частоты основных спектральных пиков: 0.05, 0.09 и 0.385 от частоты дискретизации съема данных.
Оценки СПМ в виде сглаженной периодограммы для окон Бартлетта и Хэннинга для 30 интервалов дискретизации имеют вид:
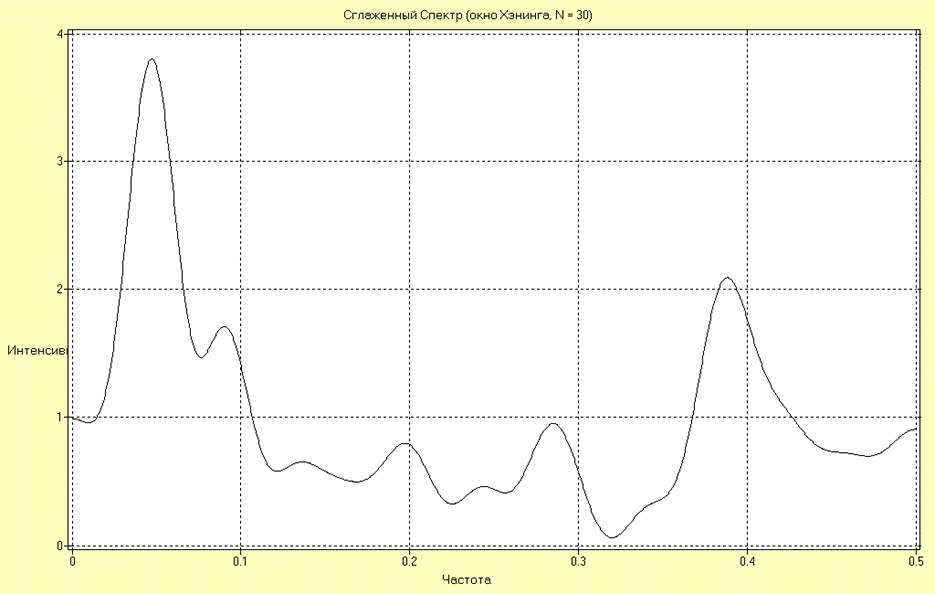
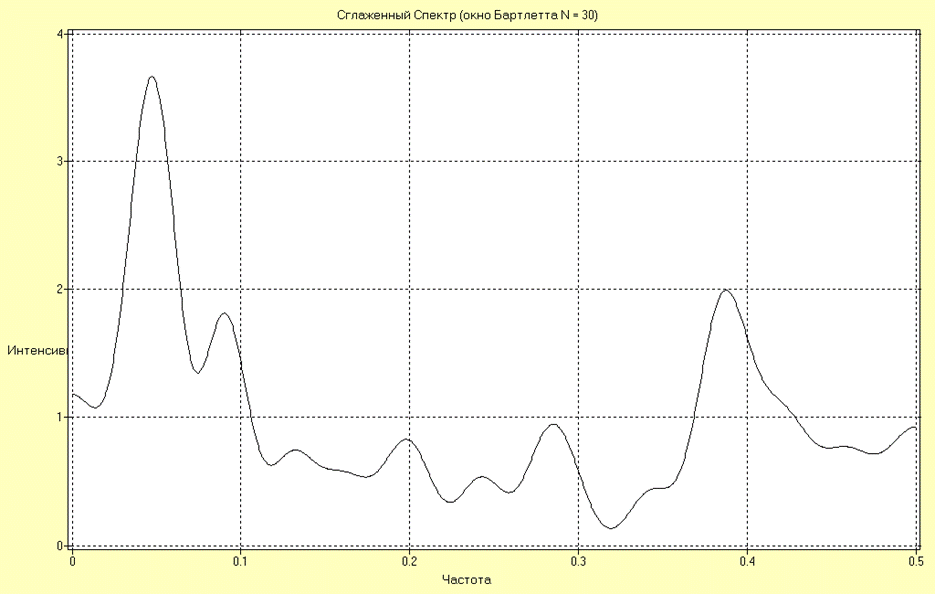
Полученные оценки подтверждают сделанный вывод относительно спектрального состава рядов.
Т.о. в основная мощность исследуемого ряда сосредоточена на частоте 0.05 от частоты дискретизации. Кроме того, в состав ряда входят две гармоники с частотами 0.09 и 0.385 меньшей мощности. так же можно сделать вывод о наличии фоновой помехи мощностью 0.5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.