Исследование стационарности ряда SI002
В результате анализа ряда оценок математического ожидания и дисперсии с помощью критериев проверки случайности были получены следующие результаты:
Тесты на Случайность
Медианный Тест
Переменная Кол-во Серий P-Значение Длина Серий P-Значение
l2_p3.ds2 5 0.7388826804 3 0.826171875
l2_p3.ms2 1 0.002699796063 5 0.216796875
Поворотных Точек Тест
Переменная Поворотных Точек Сред.Значение Стан.Отклон.
l2_p3.ds2 4 5.333333333 1.455555556
l2_p3.ms2 2 5.333333333 1.455555556
Up & Down Тест
Переменная Кол-во Серий P-Значение Длина Серий P-Значение
l2_p3.ds2 5 0.09737058403 4 0.2341666667
l2_p3.ms2 3 0.0009148792184 5 0.0429976852
Аббе Тест
Переменная Статистики P-Значение
l2_p3.ds2 1.102829527 0.7383115848
l2_p3.ms2 0.154229539 0.0006273021823
Инверсий Тест
Переменная Статистики P-Значение
l2_p3.ds2 18 0.4208286405
l2_p3.ms2 34 0.03966867046
Анализируя полученные данные можно сделать следующие выводы: гипотеза о случайности наблюдений для ряда оценок математического ожидания отвергается, следовательно ряд можно считать нестационарным по математическому ожиданию.
Оценки автокорреляционной функции и спектральной плотности мощности имеют вид:
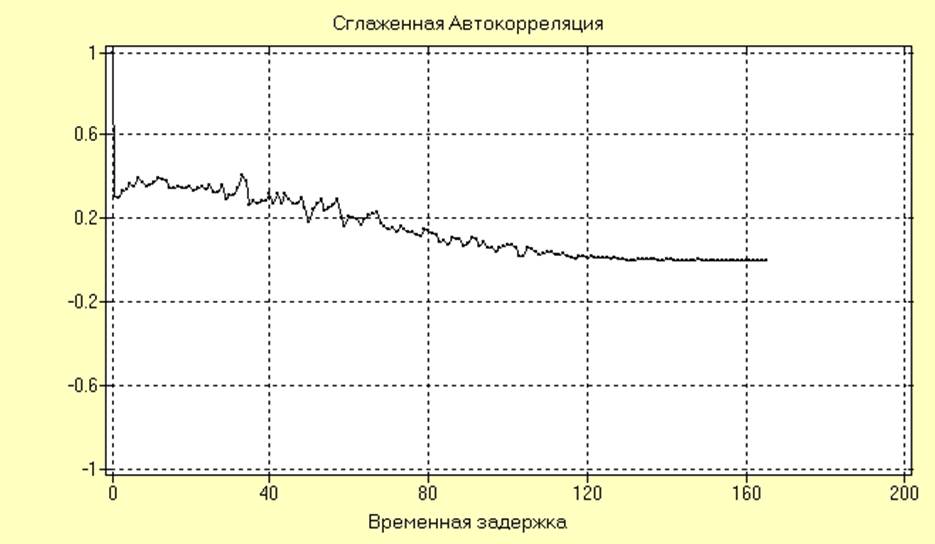
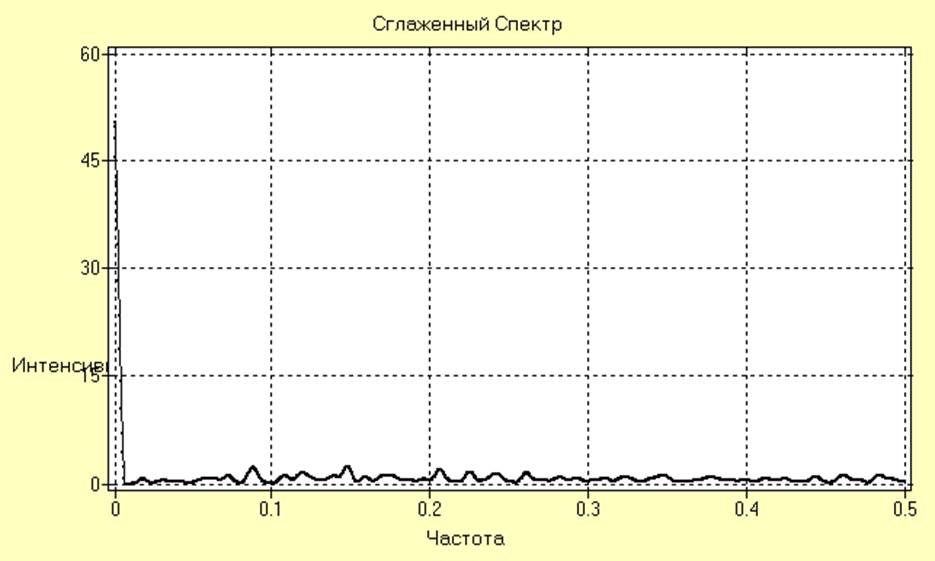
Анализирую полученные результаты можно сделать вывод о присутствии низкочастотного тренда, который является источником нестационарности по математическому ожиданию.
Т.о. тренд был обнаружен во всех 3 анализируемых рядах.
Анализ свойств рядов с удаленным трендом.
График ряда E005 после удаления тренда:
|
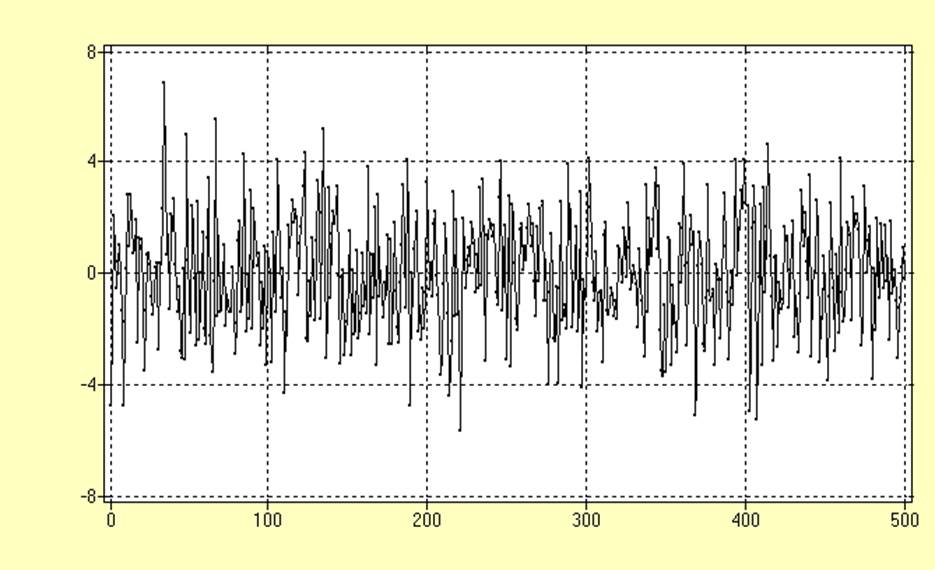
График ряда SI001 после удаления тренда:
|
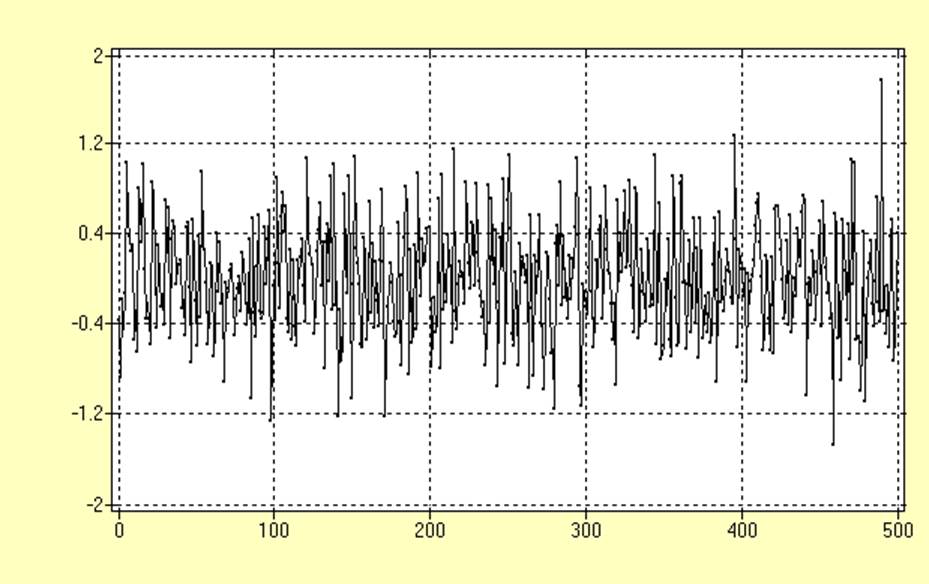
График ряда SI002 после удаления тренда:
|
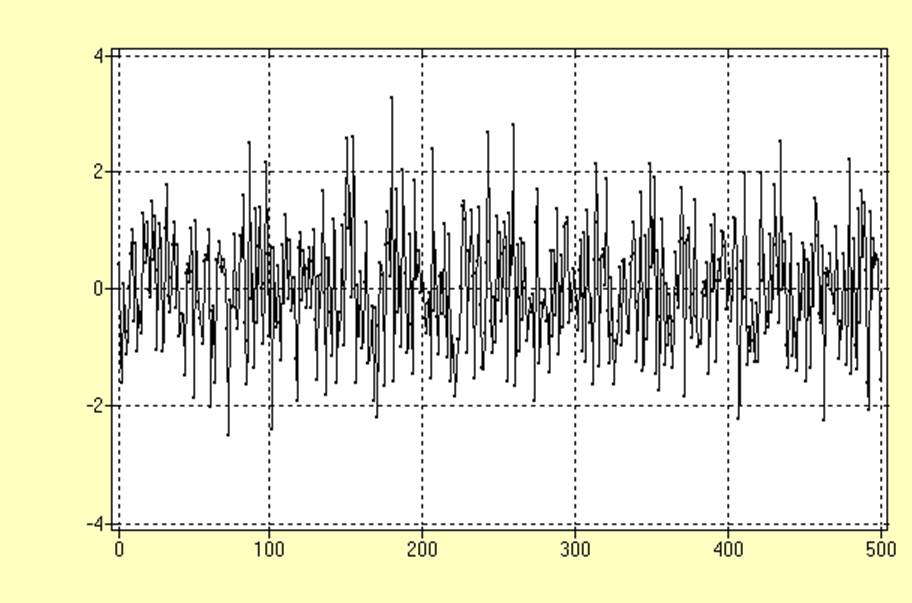
Визуальный анализ не подтверждает наличия неслучайной составляющей для рядов.
Проверка гипотезы о случайности наблюдений во всех рядах данных, с использованием критериев инверсий, серий и поворотных точек дает следующие результаты:
Медианный Тест
Переменная Кол-во Серий P-Значение Длина Серий P-Значение
lab2.e005bt 244 0.5605936745 9 0.6243684207
lab2.s001bt 245 0.6224170714 8 0.8630849597
lab2.s002bt 245 0.6224170714 9 0.6243684207
Поворотных Точек Тест
Переменная Поворотных Точек Сред.Значение Стан.Отклон.
lab2.e005bt 341 332 88.56666667
lab2.s001bt 327 332 88.56666667
lab2.s002bt 332 332 88.56666667
Инверсий Тест
Переменная Статистики P-Значение
lab2.e005bt 61887 0.7937087736
lab2.s001bt 63369 0.5942823412
lab2.s002bt 62871 0.790405196
Анализ результатов тестирования показывает, что исходная гипотеза о случайности наблюдений должна быть принята для всех 3 исследуемых рядов по данным медианного теста и теста инверсий.
Оценки АКФ и СПМ после удаления тренда для ряда Е005 принимают следующий вид:
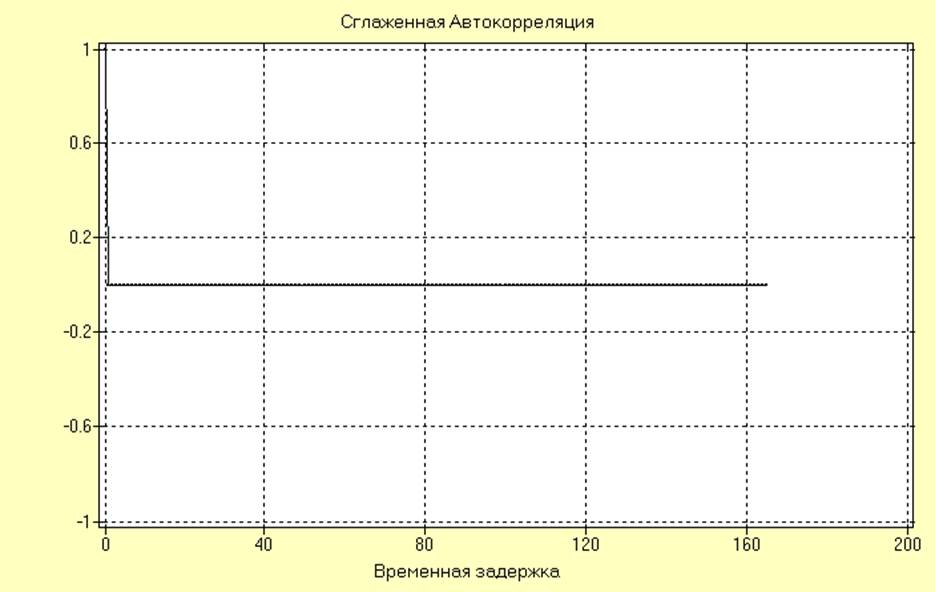
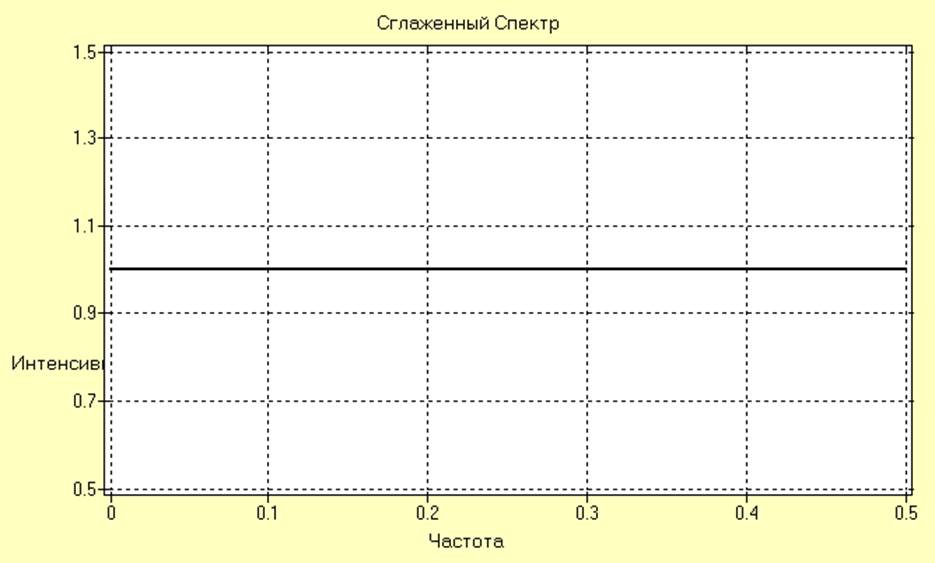
Оценки АКФ и СПМ после удаления тренда для ряда SI001 принимают следующий вид:
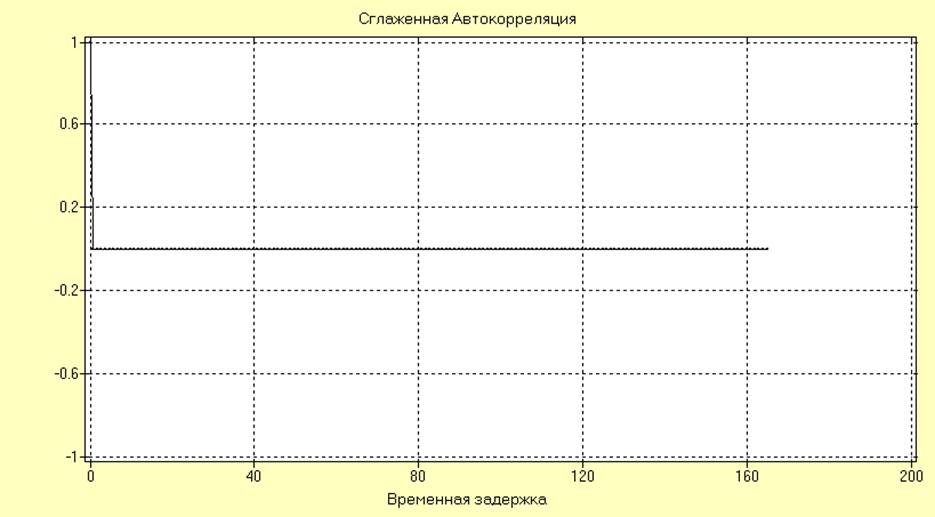
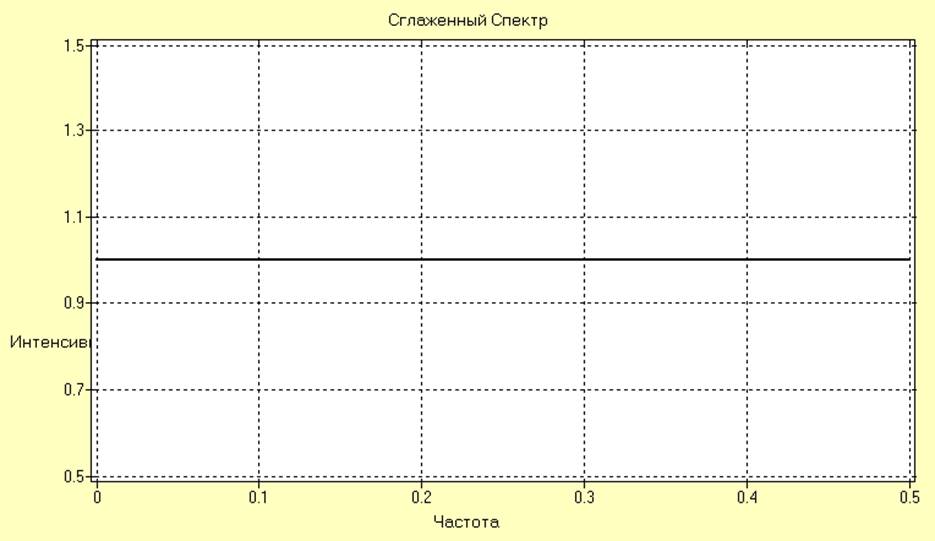
Оценки АКФ и СПМ после удаления тренда для ряда SI002 принимают следующий вид:
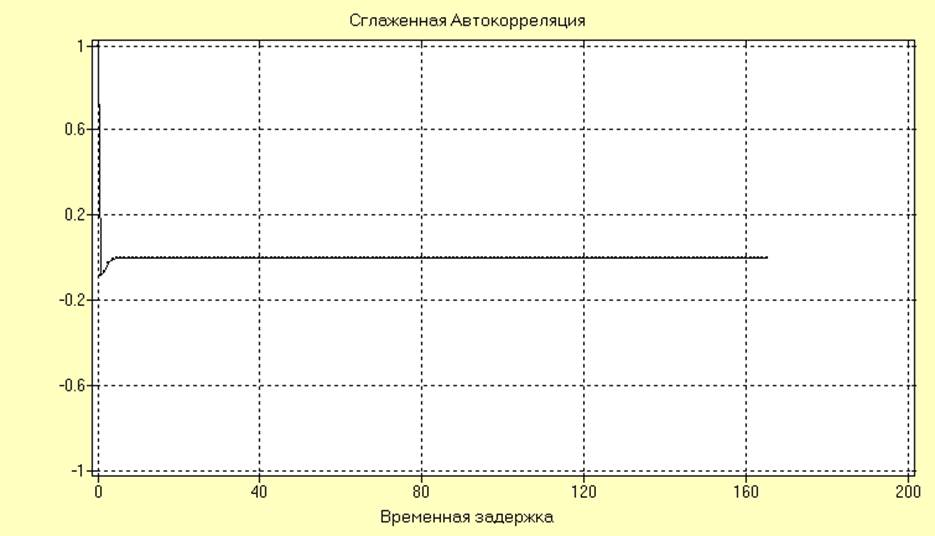
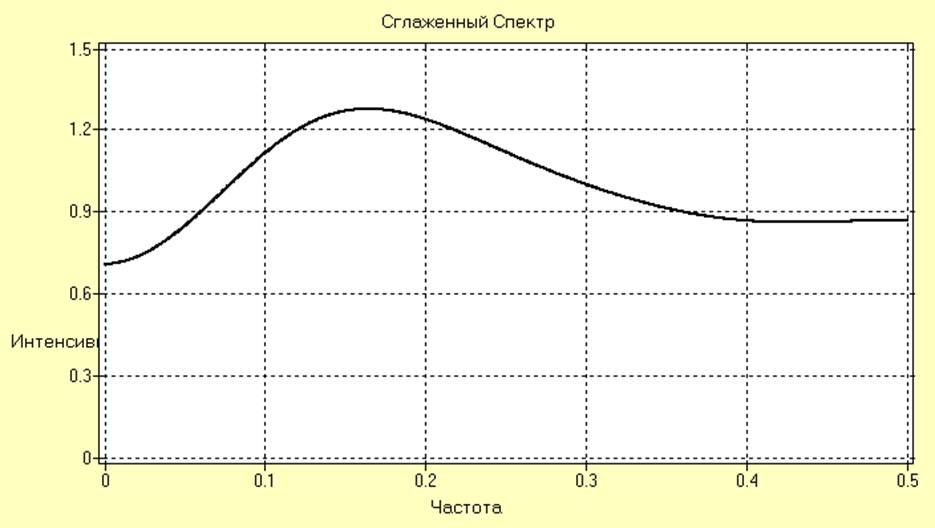
Т.о. можно констатировать удаление трендов из всех анализируемых рядов.
По результатам проведенного анализа можно сделать следующий вывод относительно свойств временных рядов и их предполагаемых моделях:
Ряд E005 представляет собой сумму детерминированной функции времени (тренда математического ожидания) и случайной широкополосной помехи. В состав ряда SI001 кроме указанных компонент входит гармонический случайный процесс. Ряд SI002 является суммой случайной широкополосной помехи и низкочастотной гармонической составляющей, которая может быть расценена как тренд.
Оценки основных числовых характеристик рядов с удаленным трендом:
lab2.si002bt lab2.si001bt lab2.e005bt
Среднее значение 0.005848911542 -0.001651702073 -0.03729043298
Медиана -0.01323155384 -0.03354320489 -0.07261304557
Максимум 2.551896572 1.458997369 6.457175255
Минимум -2.520221472 -1.433649659 -6.444069862
Дисперсия 0.9990643678 0.2533992957 4.55319772
Станд.Откл. 0.9995320744 0.5033878183 2.133822326
Асимметрия 0.003164072623 0.08073124672 -0.03237630699
Эксцесс -0.4109003026 -0.0428617743 0.02021268506
Проверка гипотезы о нормальности дает следующие результаты:
Критерий Хи-Квадрат Пирсона
Переменная c:\evrista\lab2.si002bt
Распределение Статистика Степени Свободы P-Значение
Нормальное (A,B) 41.13974447 35 0.2196023911
A =0.005848911542 ,B =0.9990643678
Переменная c:\evrista\lab2.si001bt
Распределение Статистика Степени Свободы P-Значение
Нормальное (A,B) 30.49855249 35 0.6852110143
A =-0.001651702073 ,B =0.2533992957
Переменная c:\evrista\lab2.e005bt
Распределение Статистика Степени Свободы P-Значение
Нормальное (A,B) 32.57306123 35 0.5858211283
A =-0.03729043298 ,B =4.55319772
_____________________________________________________________________________
Критерий Колмогорова-Смирнова
Переменная c:\evrista\lab2.si002bt
Распределение Статистика Р-Значение
Нормальное (A,B) 0.02279132374 0.9574496503
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.