Ознакомление с системой «ЭВРИСТА», изучение способов моделирования временных рядов, методов их визуального анализа и редактирования, страница 4

          A =0.005848911542  ,B =0.9990643678   

Переменная c:\evrista\lab2.si001bt  

   Распределение        Статистика      Р-Значение

Нормальное (A,B)        0.03116157389   0.7165655592   

          A =-0.001651702073 ,B =0.2533992957   

Переменная c:\evrista\lab2.e005bt   

   Распределение        Статистика      Р-Значение

Нормальное (A,B)        0.02464520609   0.9217243982   

          A =-0.03729043298  ,B =4.55319772

Анализ результатов тестирования показывает, что распределение наблюдений в полученных рядах близко к нормальному.

Часть 3.

Анализ наличия тренда и колебательной составляющей в исследуемых рядах.

Сглаженная периодограмма для ряда SI0001 имеет вид:

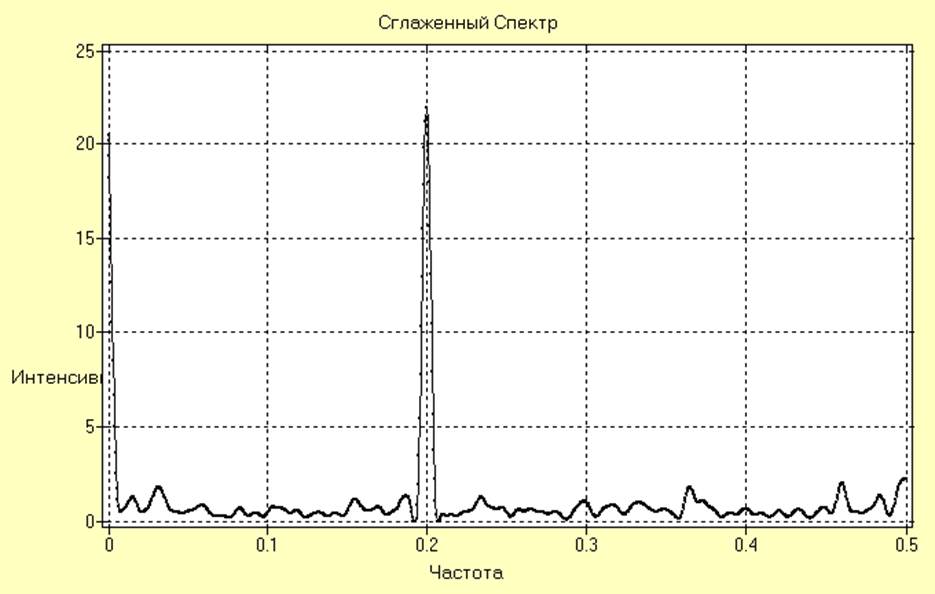
Анализ полученных результатов показывает, что в состав исследуемого ряда входят широкополосная случайная помеха, тренд, обуславливающий дрейф математического ожидания, и гармонический сигнал.

Сглаженная периодограмма для ряда E005 имеет вид:

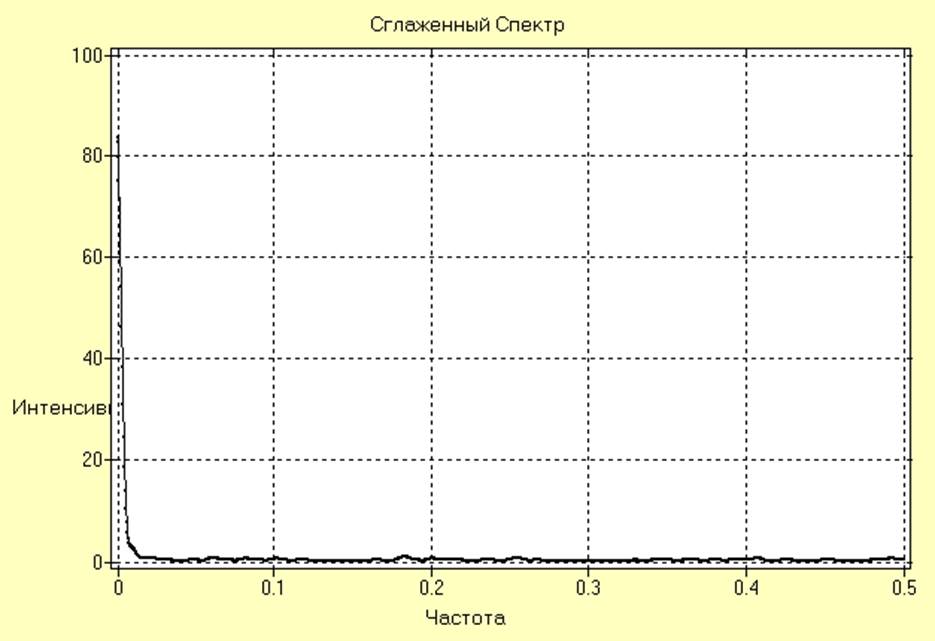
 Анализ полученных результатов показывает, что в состав исследуемого ряда входят широкополосная случайная помеха и тренд, обуславливающий дрейф математического ожидания.

Дальнейший анализ будет производится для ряда E005.

Оценка порядка линейной полиномиальной регрессии.

Результаты оценки дисперсии и среднего значения разностей различных порядков:

                  lab3.e005_r1n   lab3.e005_r2n   lab3.e005_r3n

Среднее значение  0.02584890517   -0.01361322283  0.004264679113

Оценка дисперсии    7.98125247      23.92134437     80.03289937

Дисперсия           3,99062735      3,98688333      4,00164495

                  lab3.e005_r4n   lab3.e005_r5n        

Среднее значение  -0.0121142398   0.02636985273    

Оценка дисперсии  281.9553384     1021.516095          

Дисперсия         4,02793286      4,05363532

Из анализа полученных данных следует, что описать тренд можно с помощью линейной полиномиальной регрессии 2 порядка.                    

Оценки тренда

Результаты построения полиномиальной регрессии 2 порядка для исследуемого ряда дает следующие результаты:

Модель= a0+a1t^1+a2t^2

Переменная lab3.e005

Параметр  Оценка          Станд.Ошибка     T-Значение       P-Значение

a0      1.122535649      0.2675097287     4.196242337      3.214881393e-05 

a1      -0.0008410243188 0.00247641207    0.3396140444     0.7342906667    

a2      4.212036842e-05  4.804561749e-06  8.766745152      0               

Источник      Сумма Квадратов  Степ. Свободы   Среднее Знач.

Модель        14282.53283      3                4760.844278     

Ошибка        1991.740609      497              4.007526376     

Общая         16274.27344      500              32.54854689

Результаты построения простой регрессии для линейной базисной функции для исследуемого ряда дает следующие результаты:

               Модель  Y=a+b*t

  Параметр  Оценка          Станд.Ошибка     T-Значение       P-Значение

  a=       -0.6421406893    0.1924959871     3.335865328      0.0009138435437 

  b=       0.02017703952    0.0006658270025  30.30372671      0               

Источник      Сумма Квадратов  Степ. Свободы   Среднее Знач.

Модель        13974.53111      2                6987.265553     

Ошибка        2299.742337      498              4.6179565       

Общая         16274.27344      500              32.54854689

Результаты построения простой регрессии для экспоненциальной базисной функции для исследуемого ряда дает следующие результаты:

    Модель  Y=exp(a+b*t)

  Параметр  Оценка          Станд.Ошибка     T-Значение       P-Значение

  a=       1.38341682       0.1830324289     7.558315368      1.980570113e-13 

  b=       0.002556748549   0.0006330933715  4.03850153       6.227901812e-05 

Источник      Сумма Квадратов  Степ. Свободы   Среднее Знач.

Модель        37096.59406      2                18548.29703     

Ошибка        2079.179122      498              4.175058477     

Общая         39175.77318      500              78.35154635

Построенные полиномиальная регрессия 2 порядка, простая регрессия для линейной и экспоненциальной базисных функций имеют вид:

полиномиальная регрессия порядка 2	простая регрессия для линейной базисной функции
простая регрессия для экспоненциальной базисной функции

Сравнение полученных оценок:

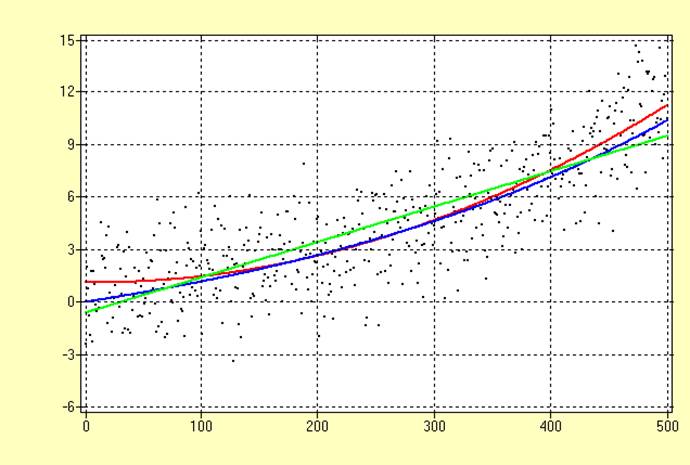
Удаление оценки тренда, полученной методом простой регрессии

для линейных базисных функций.

Сглаженная периодограмма и сглаженное изображение, полученное методом простого сколь­зящего среднего, для исследуемого ряда с удаленным трендом имеют вид:

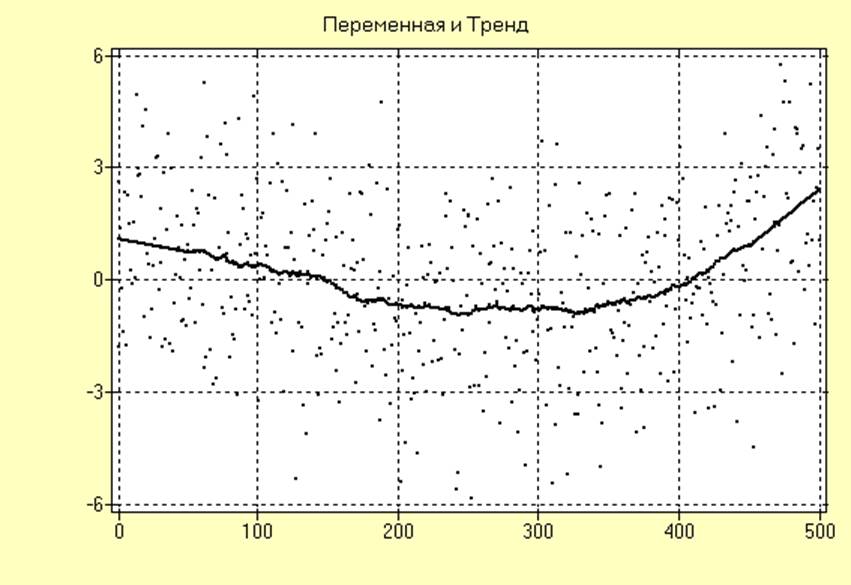
Из анализа полученных результатов следует, что качество удаления тренда довольно низкое.

Удаление оценки тренда, полученной методом простой регрессии для экспоненциальных базисных функций.

Сглаженная периодограмма и сглаженное изображение, полученное методом простого сколь­зящего среднего, для исследуемого ряда с удаленным трендом имеют вид:

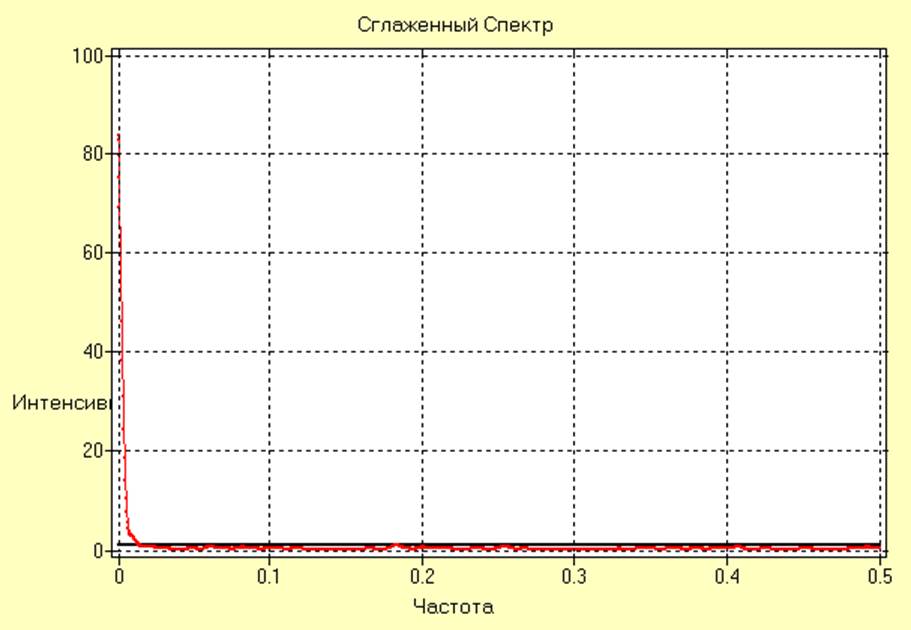
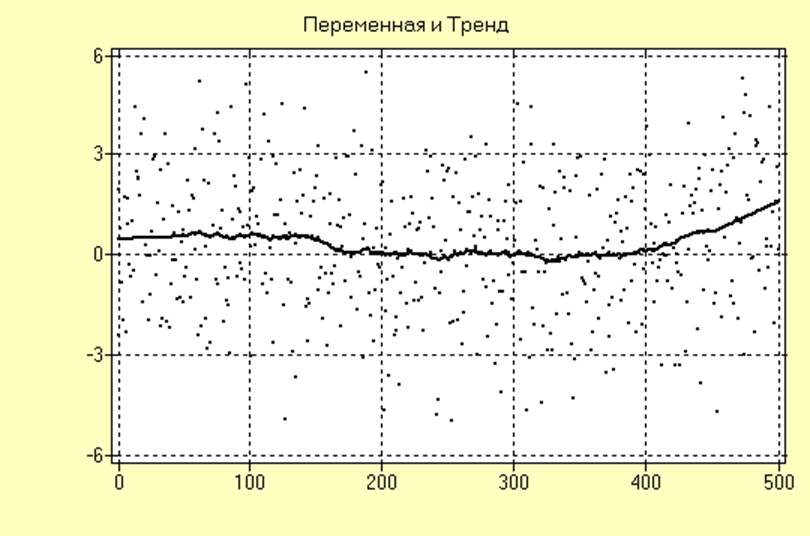
Из анализа полученных результатов следует, что качество удаления тренда улучшилось по сравнению с предыдущим случаем и является приемлемым.

Удаление оценки тренда, полученной методом полиномиальной регрессии 2 порядка.

Сглаженная периодограмма и сглаженное изображение, полученное методом простого сколь­зящего среднего, для исследуемого ряда с удаленным трендом имеют вид:

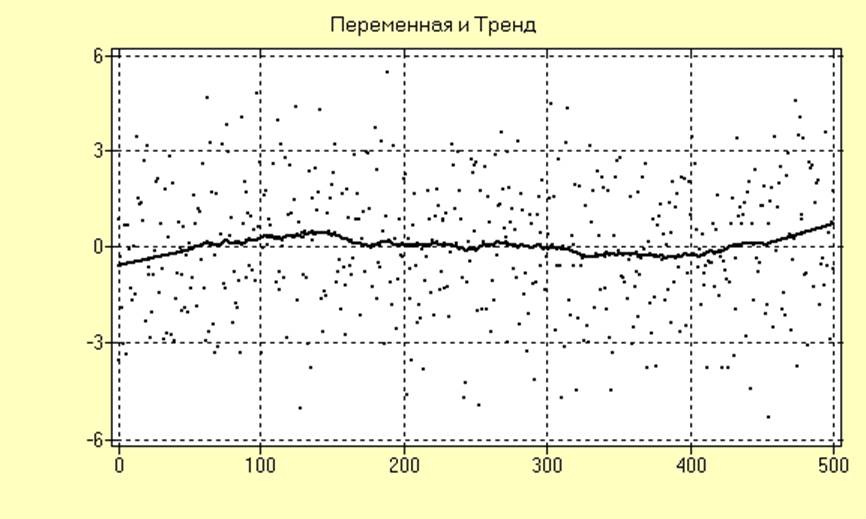
Из анализа полученных результатов следует, что качество удаления тренда стало   еще лучше.

Разделение временного ряда на компоненты с использованием цифровой фильтрации.

Для выделения обнаруженного тренда из исследуемого ряда может быть применен низкочастотный рекурсивный (тангенсный) фильтр порядка 10, АЧХ которого имеет следующий вид:

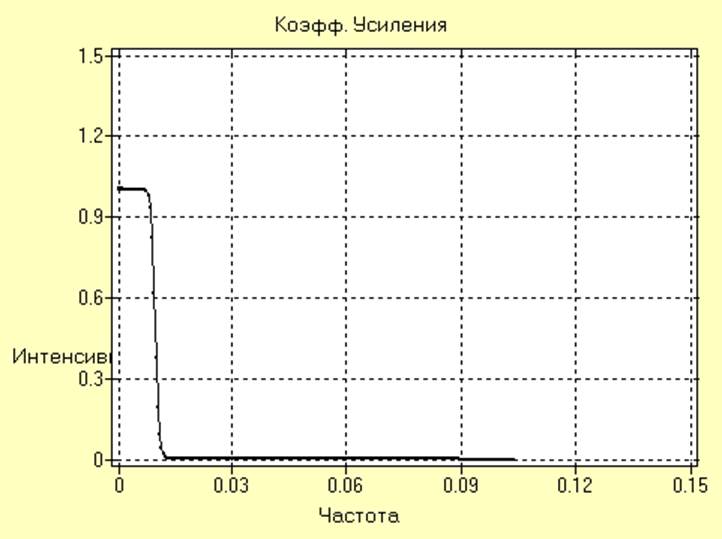
Отфильтрованный сигнал и оценка его спектральной плотности имеют вид:

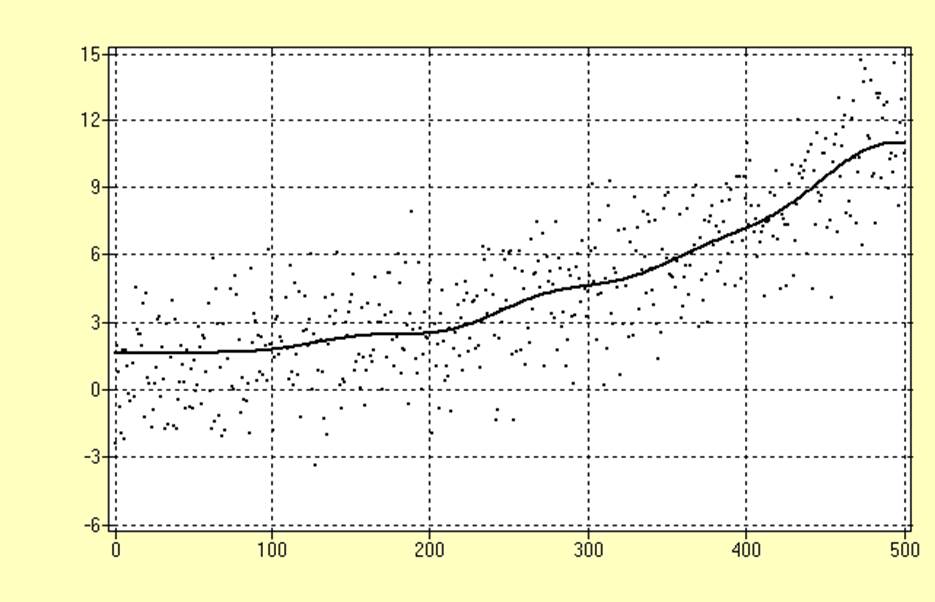
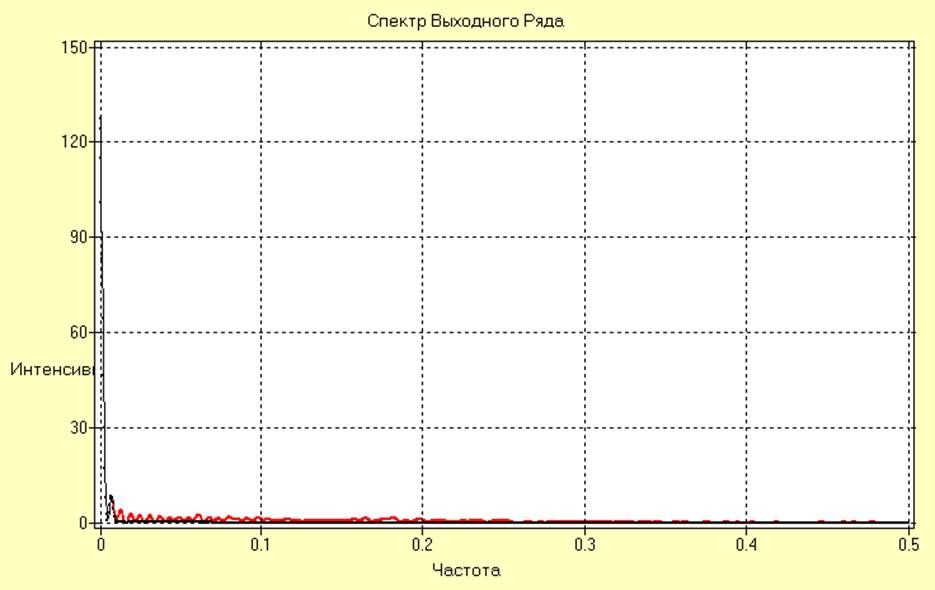
Анализируя полученные результаты, можно заметить, что цифровая фильтрация обеспечивает довольно хорошее качество выделения тренда.

Для удаления обнаруженного тренда из исследуемого ряда может быть применен высокочастотный рекурсивный (тангенсный) фильтр порядка 10, АЧХ которого имеет следующий вид:

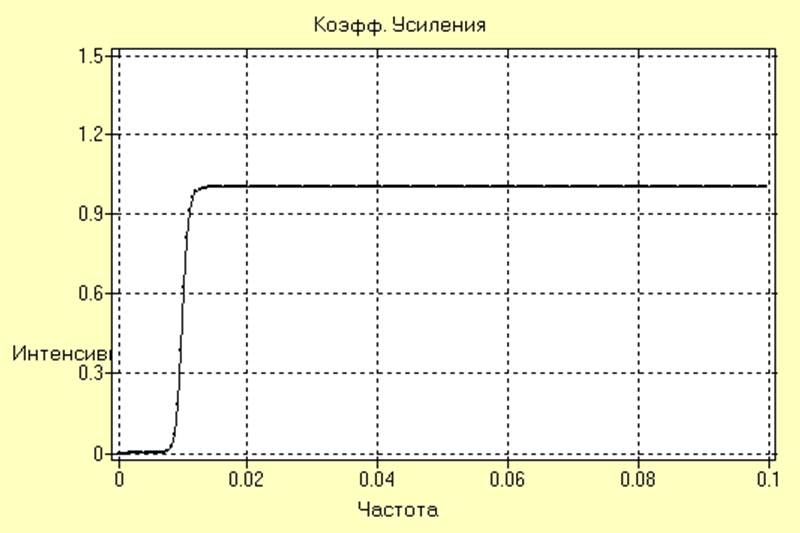
Отфильтрованный сигнал и оценка его спектральной плотности имеют вид:

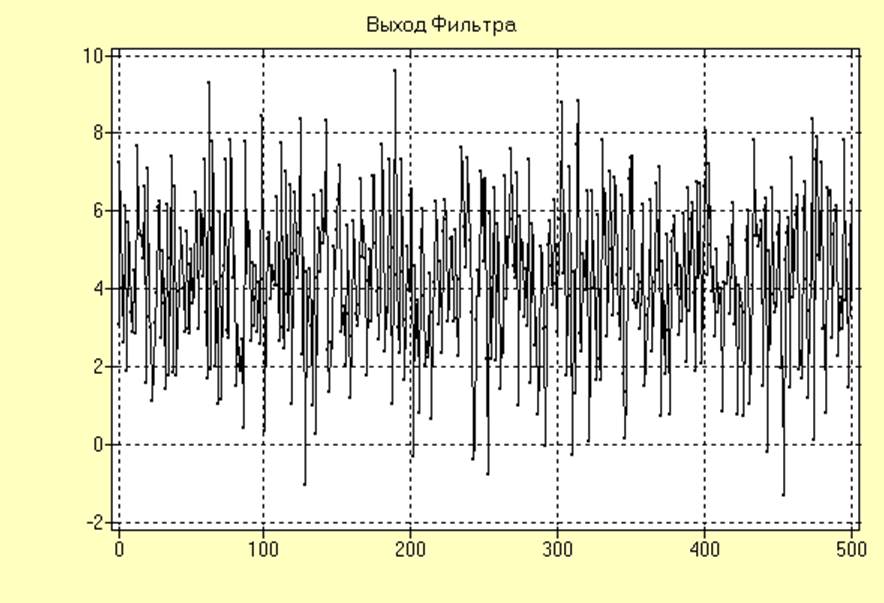
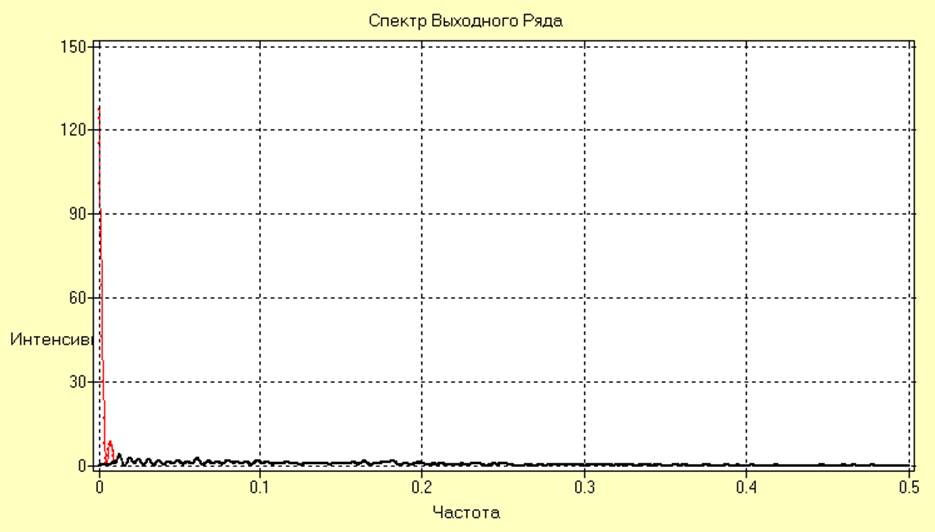
Анализируя полученные результаты, можно заметить, что цифровая фильтрация обеспечивает довольно хорошее качество удаления тренда.