Изучение алгоритмов расчета и свойств оценки авто­корреляционной функции Rхх(nT)

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Лабораторная работа № 4

по курсу анализ стохастических процессов

Цель работы

Изучение алгоритмов расчета и свойств оценки авто­корреляционной функции R_XX(nT).

Программа исследований

1. Исследовать свойства оценки автокорреляционной функции (АКФ) при n=0 (R_XX(0)), для чего:

а)  смоделировать по 10 реализаций временных рядов типа "белый" шум с интенсивностью N0=0.5 и длинами реализаций N=100 и N=900, типа авторегрессии первого порядка с параметром АР(1)=0.1, дис­персией шума s2=1 и длинами реализаций N=100 и N=1000,

б)  по всем реализациям рассчитать оценку R_XX(0) и исследовать статистические свойства этих оценок по выборкам объема 10,

в)  результаты расчетов свести в таблицы по каждому виду ряда.

2. Рассчитать R_XX(nT) и ее оценки для временных рядов заданного вида, для этого:

а)  смоделировать временные ряды типа АР первого порядка с пара­метрами АР(1)=0.1, АР(1)=-0.1 и АР(1)=-0.9 при длинах реализации N=100 и N=900 для каждого значения параметра и записать их в каталог,

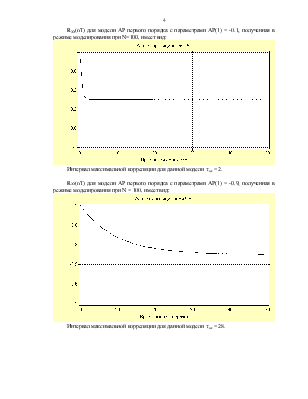
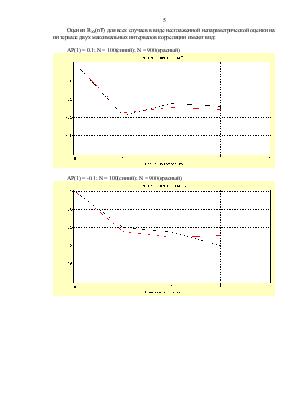
б)  в режиме моделирования рассчитать R_XX(nT) для моделей всех ви­дов при N=100 и оценить максимальный интервал корреляции (возможно использовать режим «ЛУПА»),

в)  получить оценки R_XX(nT) для всех случаев в виде несглаженной не-параметрической оценки c заданным числом ординат на интервале двух максимальных интервалов корреляции.

3. Исследовать поведение оценки R_XX(nT) временных рядов в зависи­мости от длины реализации и характера процесса, для этого:

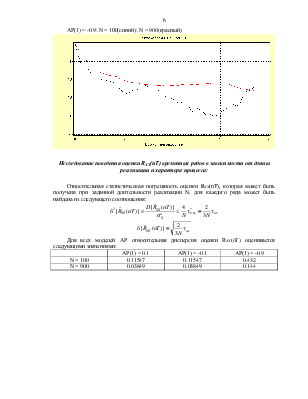
а)  оценить относительную дисперсию оценки R_XX(nT), которая мо­жет быть получена при заданной длительности реализации для каждого ряда,

б)  в режиме "ЛУПА" сравнить оценки R_XX(nT) и АКФ модели на ин­тервале максимальной корреляции (результаты п.п.2-б и 2-в) и сделать вы­воды о качестве оценки,

в)  вывести три рисунка на печать, на каждом рисунке должны быть три графика, относящиеся к ряду определенного типа: R_XX(nT) модели, оценки R_XX(nT) для N=100 и  N=900 на интервале максимальной корреля­ции.

4. Исследовать возможность обнаружения колебательной составляю­щей ряда с помощью R_XX(nT), используя временные ряды разных типов, для этого

а)  смоделировать ряды,

б)  рассчитать сглаженную оценку R_XX(nT),

в)  сделать выводы о возможности провести первоначальный анализ состава временного ряда, используя автокорреляционную функцию.

5. Исследовать корреляционные свойства модели процесса типа «бе­лый» шум до и после сглаживания методом простого скользящего сред­него. Для этого использовать реализацию временного ряда из п.1 при N=900, процедуру сглаживания по m=5 и m=25 точкам и алгоритм непара­метрического оценивания сглаженной автокорреляционной функции. Вы­вести в файл для печати оценки автокорреляционных функций исходного и двух сглаженных временных рядов. Объяснить вид оценки АКФ и изменения в ней после сглаживания.

Исходные данные для проведения исследований

SI01.N200 ® SIN(0.1*2*pi*CASE(200)),

SI01.NO200 ®SIN(0.2*pi*CASE(200))+0.5*NOISE(200),

SI01.BNO200 ® SIN(0.2*pi*CASE(200))+2*NOISE(200),

SS00501.NO200 ® SI01.BNO200+SIN(0.005*2*pi*CASE(200)).

Результаты исследований

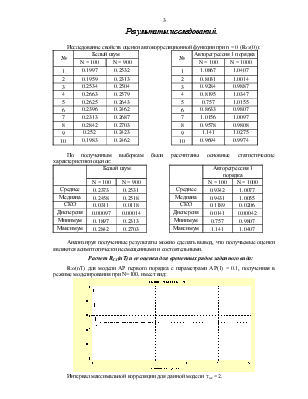
Исследование свойств оценки автокорреляционной функции при n = 0 (R_XX(0)):

По полученным выборкам были рассчитаны основные статистические характеристики оценок: