Изучение алгоритмов расчета и свойств оценки авто­корреляционной функции Rхх(nT), страница 2

	Белый шум				Авторегрессия 1 порядка
	N = 100	N = 900			N = 100	N = 1000
Среднее	0.2373	0.2531		Среднее	0.9342	1.0077
Медиана	0.2458	0.2518		Медиана	0.9431	1.0055
СКО	0.0311	0.0118		СКО	0.1189	0.0206
Дисперсия	0.00097	0.00014		Дисперсия	0.0141	0.00042
Минимум	0.1897	0.2313		Минимум	0.757	0.9807
Максимум	0.2842	0.2703		Максимум	1.141	1.0407

Анализируя полученные результаты можно сделать вывод, что получаемые оценки являются асимптотически несмещенными и состоятельными.

Расчет R_XX(nT) и ее оценки для временных рядов заданного вида:

R_XX(nT) для модели АР первого порядка с пара­метрами АР(1) = 0.1, полученная в режиме моделирования при N=100, имеет вид:

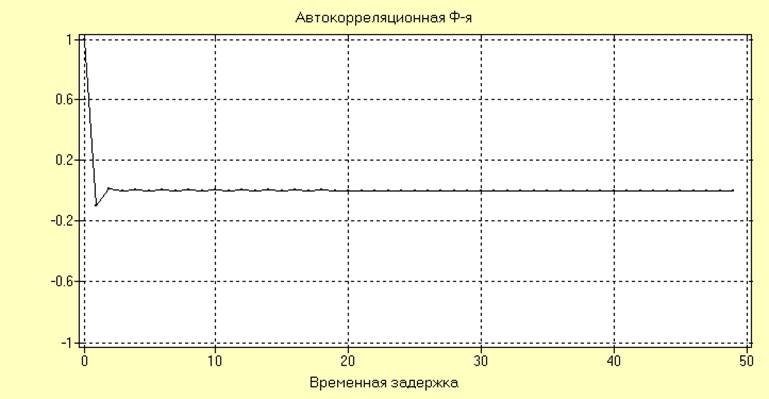
Ин­тервал максимальной корреляции для данной модели = 2.

R_XX(nT) для модели АР первого порядка с пара­метрами АР(1) = -0.1, полученная в режиме моделирования при N=100, имеет вид:

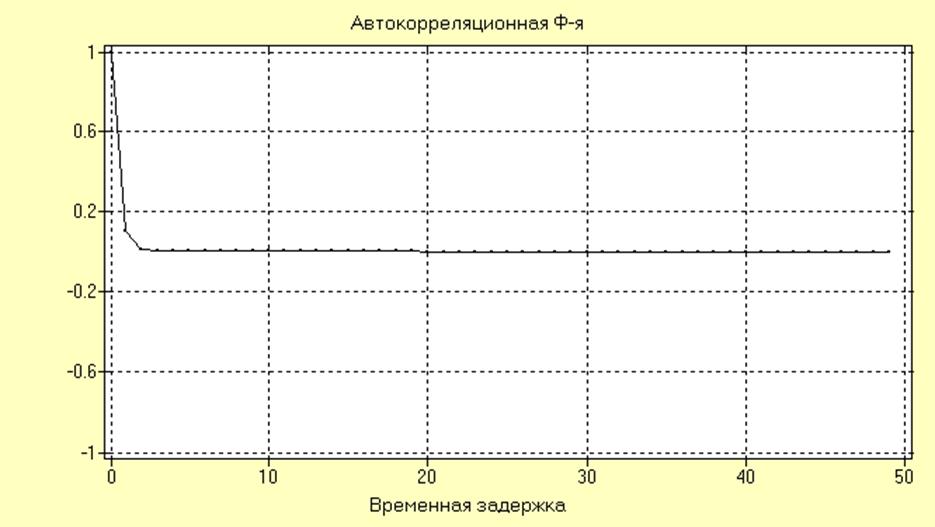
Ин­тервал максимальной корреляции для данной модели = 2.

R_XX(nT) для модели АР первого порядка с пара­метрами АР(1) = -0.9, полученная в режиме моделирования при N = 100, имеет вид:

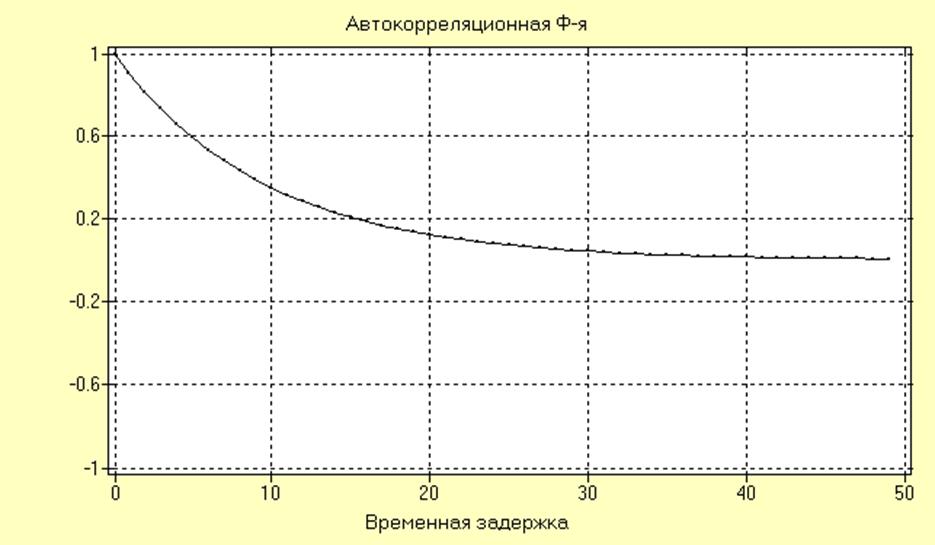
Ин­тервал максимальной корреляции для данной модели = 28.

Оценки R_XX(nT) для всех случаев в виде несглаженной непараметрической оценки на интервале двух максимальных интервалов корреляции имеют вид:

АР(1) = 0.1; N = 100(синий); N = 900(красный)

АР(1) = -0.1; N = 100(синий); N = 900(красный)

АР(1) = -0.9; N = 100(синий); N = 900(красный)

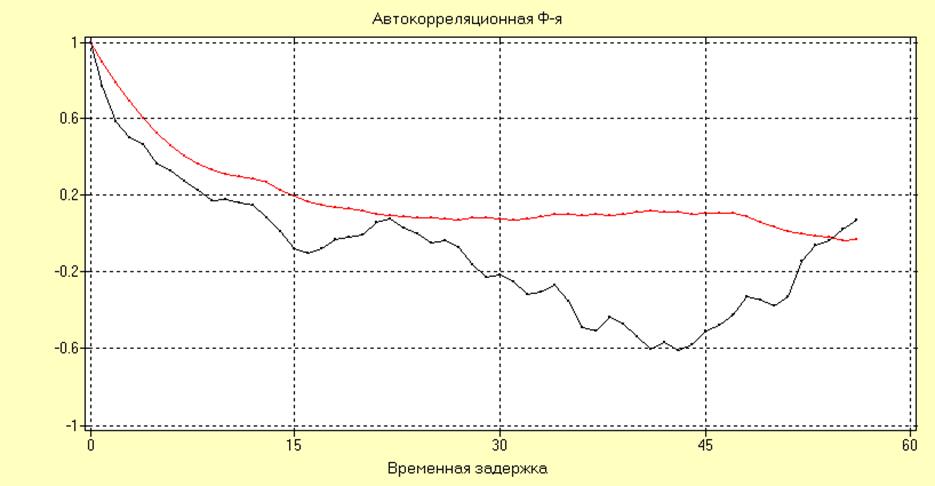
Исследование поведения оценки R_XX(nT) временных рядов в зависи­мости от длины реализации и характера процесса:

Относительная статистическая погрешность оценки R_XX(nT), которая мо­жет быть получена при заданной длительности реализации N, для каждого ряда может быть найдена из следующего соотношения:

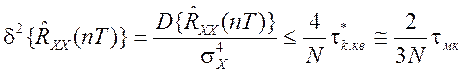
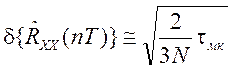
Для всех моделей АР относительная дисперсия оценки R_XX(nT) оценивается следующими значениями:

	АР(1) = 0.1	АР(1) = -0.1	АР(1) = -0.9
N = 100	0.11547	0.11547	0.432
N = 900	0.03849	0.03849	0.144

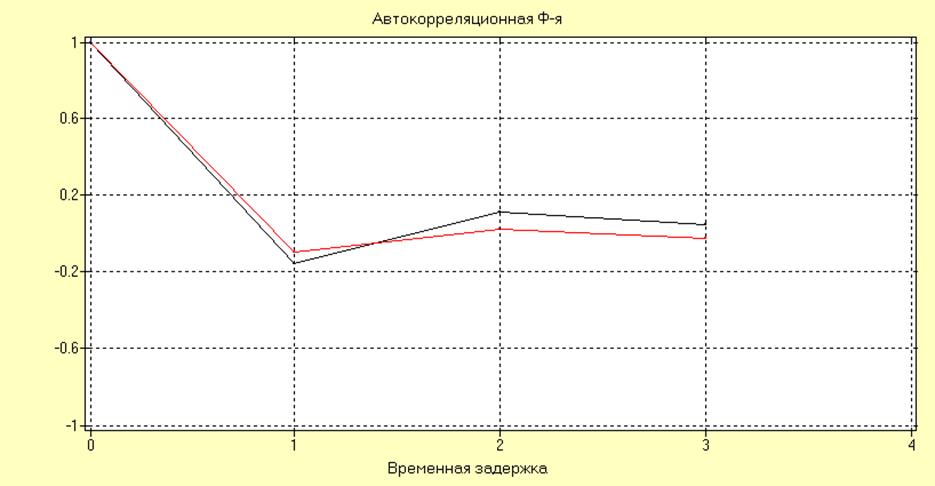
Сравнение оценки R_XX(nT) и АКФ моделей на ин­тервале максимальной корреляции дает следующие результаты:

АР(1) = 0.1; N=100(черный), N=900(красный), теоретическая(синий)

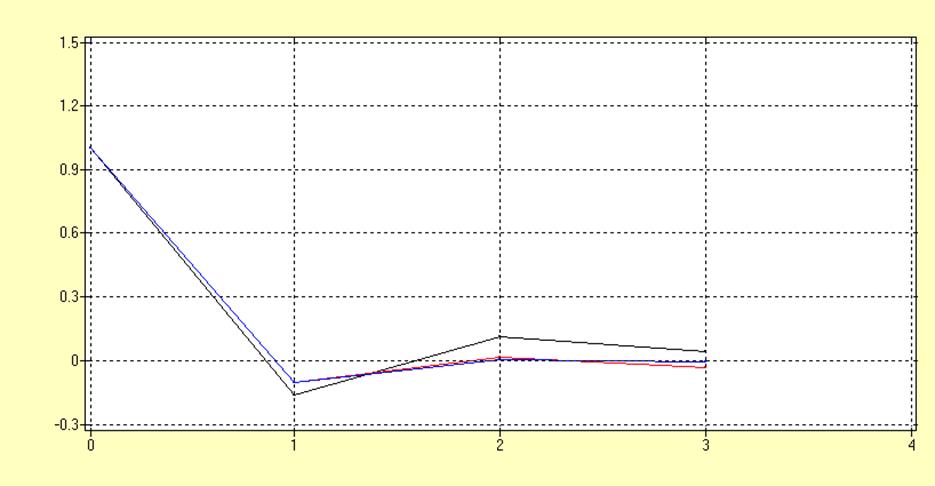
Оценка, полученная по выборке большей, длины является более точной, что соответствует теории. Анализируя графики можно предположить, что оценка автокорреляционной функции является асимптотически несмещенной и состоятельной.

АР(1) = -0.1; N=100(черный), N=900(красный), теоретическая(синий)

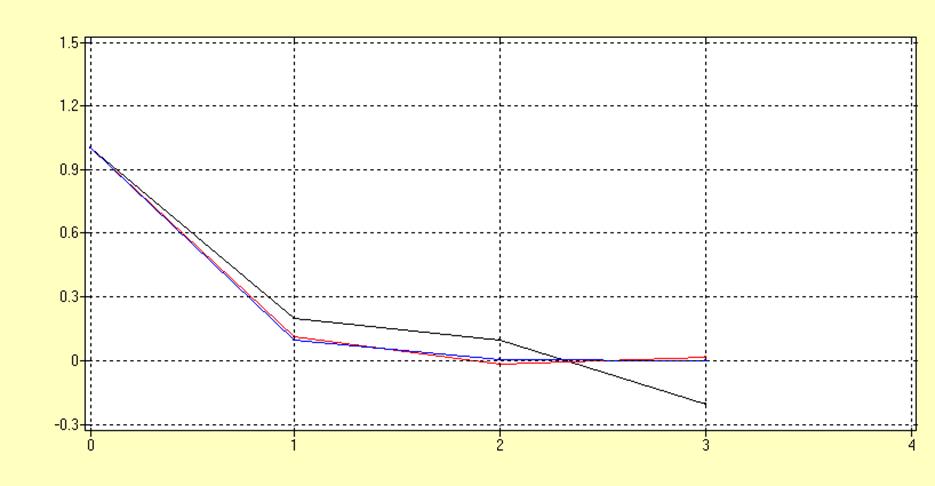
Оценка, полученная по выборке большей, длины является более точной, что соответствует теории. Анализируя графики можно предположить, что оценка автокорреляционной функции является асимптотически несмещенной и состоятельной.

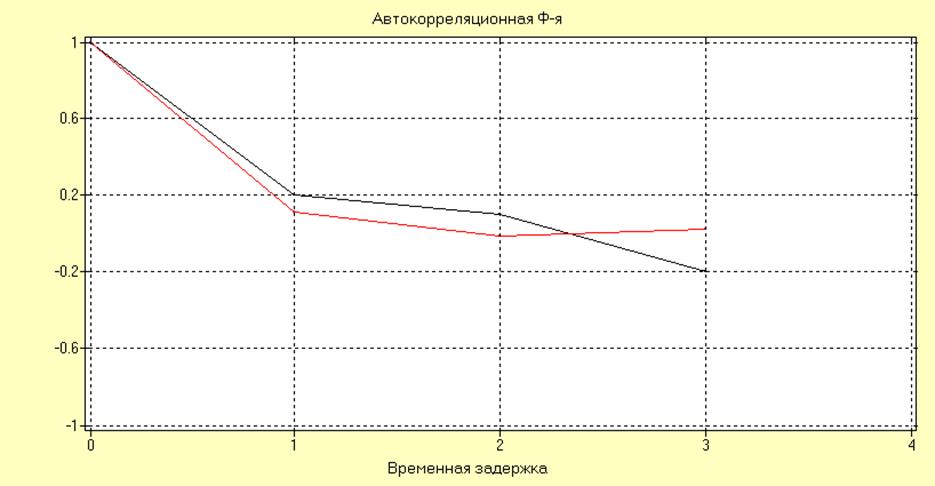
АР(1) = -0.9; N=100(черный), N=900(красный), теоретическая(синий)

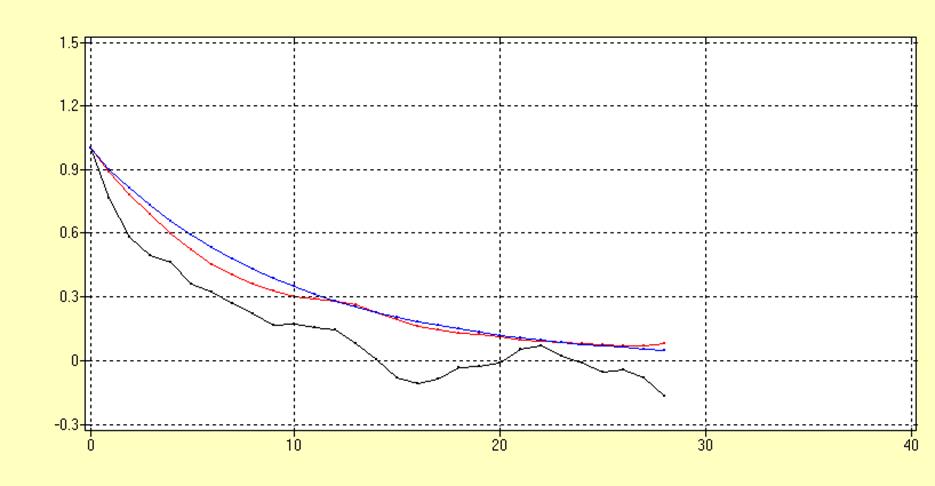
Оценка, полученная по выборке большей, длины является более точной, что соответствует теории. Анализируя графики можно предположить, что оценка автокорреляционной функции является асимптотически несмещенной и состоятельной.

Исследование возможности обнаружения колебательной составляю­щей ряда с помощью R_XX(nT)

Сглаженная оценка R_XX(nT) для ряда SI01.N200 = SIN(0.1*2*pi*CASE(200)) имеет вид:

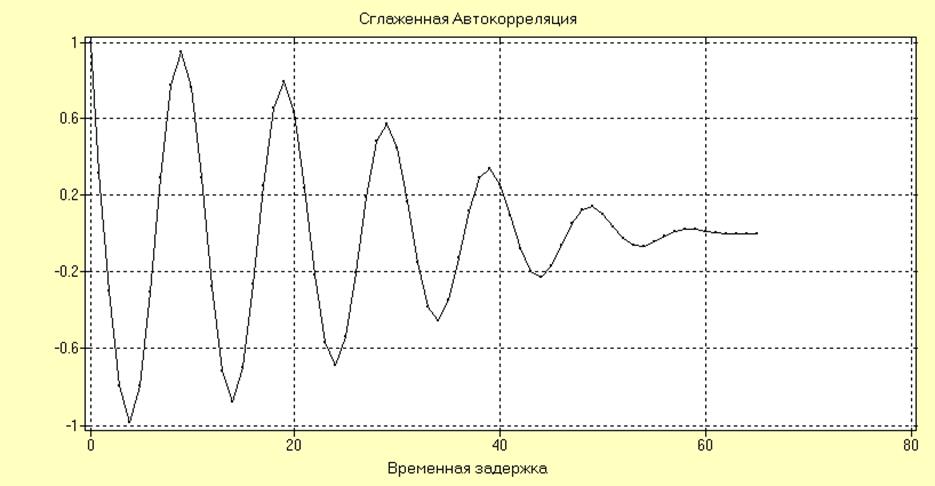
Из графика видно, что оценка АКФ для исследуемого процесса имеет ярко выраженный колебательный характер, что говорит о наличии колебательной составляющей в исследуемом ряде.

Сглаженная оценка R_XX(nT) для ряда SI01.NO200 ® SIN(0.2*pi*CASE(200)) + 0.5*NOISE(200) имеет вид:

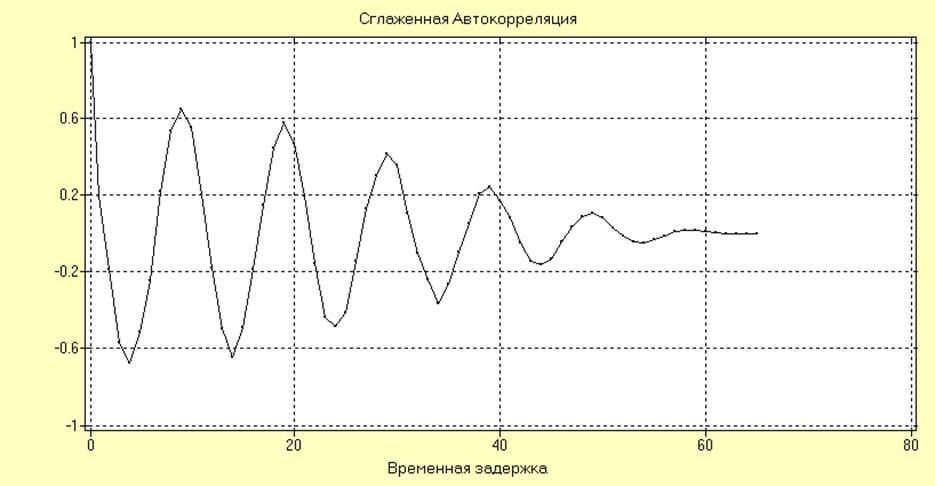
Из графика видно, что оценка АКФ для исследуемого процесса имеет ярко выраженный колебательный характер. Уменьшение амплитуды колебаний в сравнении с предыдущим случаем свидетельствует об уменьшении коррелированности отсчетов за счет добавления широкополосной помехи.

Сглаженная оценка R_XX(nT) для ряда SI01.BNO200 ® SIN(0.2*pi*CASE(200)) + 2*NOISE(200) имеет вид:

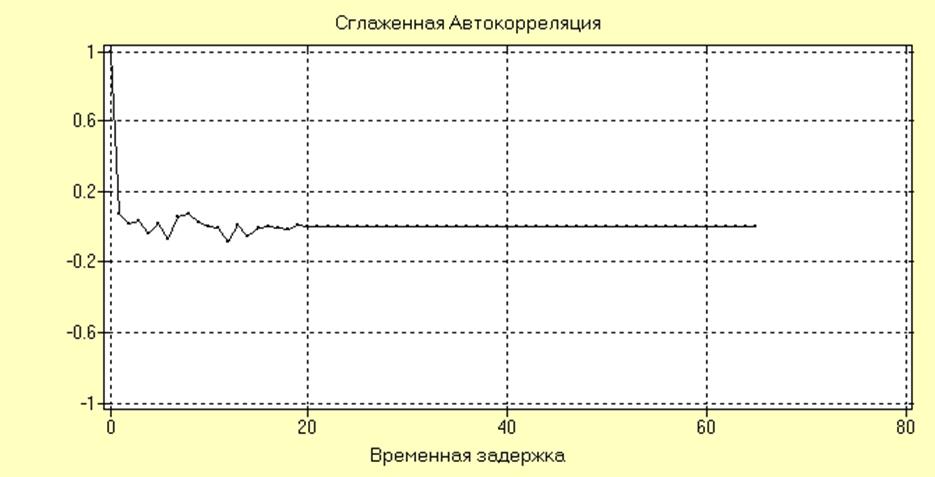
Как видно из графика АКФ исследуемого ряда близка к АКФ белого шума, однако в области малых интервалов между ординатами имеется некоторая корреляция. Анализ данной корреляции затруднен в силу малой амплитуды сигнала на фоне широкополосной помехи.

Сглаженная оценка R_XX(nT) для ряда SS00501.NO200 ® SI01.BNO200 + SIN(0.005*2*pi*CASE(200)) имеет вид:

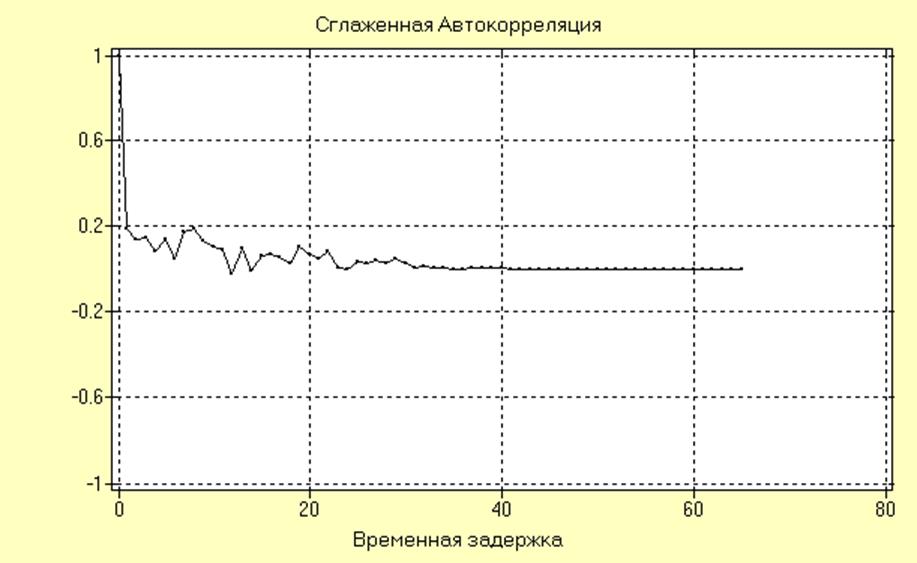
Как видно из графика АКФ исследуемого ряда близка к АКФ белого шума, однако в области малых интервалов между ординатами имеется некоторая корреляция. Анализ данной корреляции затруднен в силу малой амплитуды сигнала на фоне широкополосной помехи. Если сравнить данную АКФ с предыдущей, то нетрудно заметить, что корреляция увеличилась. Это свидетельствует о том, что в данном процессе соотношение синал/шум выше, чем в предыдущем.

Исследование корреляционных свойств модели процесса типа «бе­лый» шум до и после сглаживания методом простого скользящего сред­него.

Оценки автокорреляционных функций исходного и двух сглаженных временных рядов имеют вид:

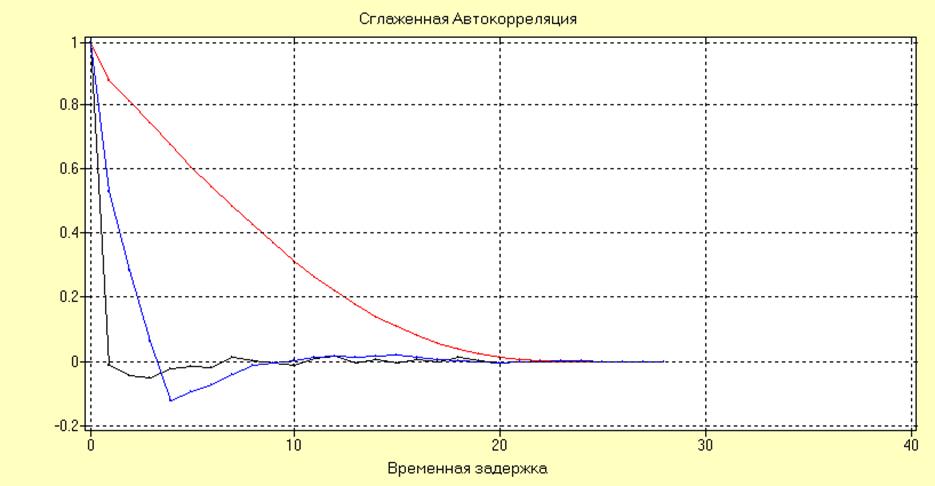
Анализируя полученные результаты можно сделать вывод, о том что сглаживание методом простого скользящего среднего вносит дополнительную коррелированность рядов, причем интервал максимальной корреляции равен количеству точек, по которому производится сглаживание.