Исследование переходных процессов в схемах с распределенными параметрами

ЛАБОРАТОРНАЯ РАБОТА № 3

ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СХЕМАХ

 С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

ЦЕЛЬ РАБОТЫ

Ознакомиться с методикой исследования переходных процессов в схемах с распределенными параметрами. Для заданного варианта схемы разработать математическую модель, реализовать ее на ПЭВМ, рассчитать переходный процесс и провести анализ полученных результатов.

ПРОГРАММА РАБОТЫ

1. Для  заданного варианта схемы с распределенными  параметрами      (табл. П.3) разработать математическую модель, описывающую переходные процессы в исследуемой схеме.

2. Реализовать разработанный алгоритм в виде программы для ПЭВМ.

3. Рассчитать  во временном диапазоне от 0 до 40 мкс изменения напряжения в узлах схемы  при воздействии заданного импульса напряжения.

4. Составить отчет, который должен содержать:

-  исходную расчетную схему и математическую модель для исследования  

          волновых процессов  в заданной схеме;

-  распечатку программы разработанного алгоритма;

-  расчетные кривые изменения напряжения в исследуемых узлах схемы ;

-  анализ полученных результатов.

ПОЯСНЕНИЯ К РАБОТЕ

          При исследовании электромагнитных переходных процессов в электрической сети, последнюю можно представить в виде совокупности узлов, включающих элементы с сосредоточенными параметрами (моделирующими различное высоковольтное оборудование), соединенные между собой элементами с распределенными параметрами (воздушными или кабельными линиями). При этом в отличие от схем с сосредоточенными параметрами, где любая коммутация в схеме приводит к мгновенному изменению напряжения и тока во всех узлах цепи, в схемах, содержащих участки линий,  изменения напряжений и токов в узлах  происходят с некоторой задержкой по времени, поскольку узлы схемы соединены между собой элементами с распределенными параметрами,  по которым электромагнитная волна распространяется с конечной скоростью, определяемой свойствами диэлектрической среды (воздуха для воздушной линии, элегаза – для газоизолированных линий, бумажно-пропитанная и пластмассовая изоляция – для кабельных линий). Определение изменения напряжения и токов в узлах такой схемы осуществляется на базе математической модели, которая содержит уравнения,  описывающие переходные процессы в узлах схемы и уравнения длинной линии, связывающих эти узлы.

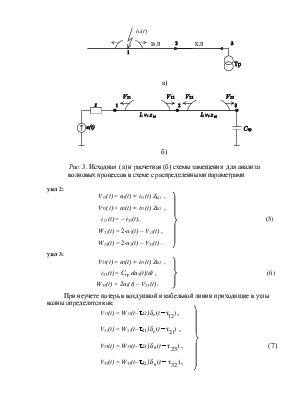
          Рассмотрим математическую модель, описывающую переходные процессы в схеме, содержащей лишь два узла (рис.1), соединенные участком линии с параметрами l , n и Z_В , где l  - длина линии, n - скорость распространения электромагнитной волны и  Z_В  - волновое сопротивление линии.

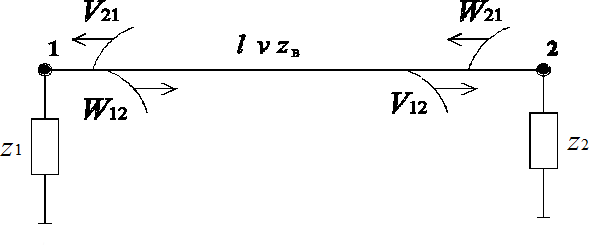
Рис. 1.  К выводу уравнений, описывающих волновые

                      процессы в электрических сетях

          При использовании метода обобщенных бегущих волн уравнения для узлов схемы записываются в виде

                              V₂₁(t) = u₁(t) + i₂₁(t) Z_В ,

                             V₁₂(t) = u₂(t) + i₁₂(t) Z_В ,

                               i₁(t)  = f₁ [u₁(t)] ,                                                                       (1)                                              i₂(t)  = f ₂[u₂(t)] ,                                                                               

где V₁₂(t) и V₂₁(t) – обобщенные волны, набегающие на узлы 1 и  2, 

u₁(t), u₂(t) и  i₁(t), i₂(t) - напряжения и токи в соответствующих узлах.

          Уравнения (1) позволяют в каждый момент времени при известных значениях обобщенных волн, набегающих на узлы 1 и 2, определить напряжения и токи в этих узлах. Затем в этих узлах определяются обобщенные отраженные волны:    

                   W₂₁(t) = 2u₂(t) – V₁₂(t) ,   

                   W₁₂(t) = 2u₁(t) – V₂₁(t) .                                                                    (2)

          При неучете  потерь в линии (R=G=0) отраженные волны будут падающими для узлов, через времена, равные временам пробега волн по линии, т.е. уравнения, связывающие узлы 1 и 2, записываются в виде

                       V₁₂(t) = W₁₂(t–t₁₂),

                       V₂₁(t)=W₂₁(t–t₂₁),                                                 (3) 

где t₁₂= t₂₁ = l/n - время пробега волны по линии длиной l,

        0при  t < t₁₂ ,

 =  

                                         1  при,  t > t₁₂  - обобщенная единичная функция.

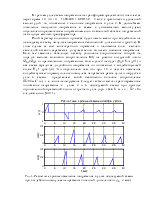
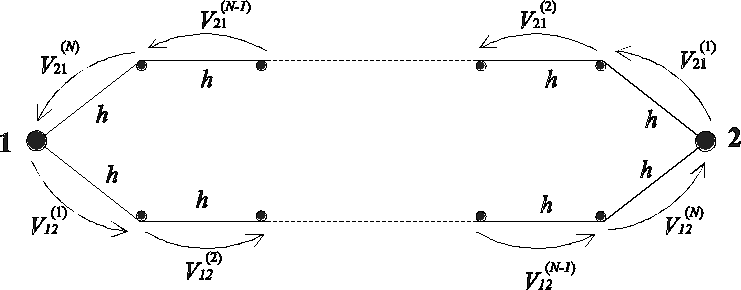
          Таким образом, математическая модель расчетной задачи состоит из уравнений (1), описывающих переходные процессы в узлах исследуемой схемы, и уравнений (2) и (3), описывающих волновые процессы в линии. На рис.2 приведена блок-схема и алгоритм, имитирующий  движение прямых и обратных волн. Из рисунка видно, что для моделирования движения этих волн требуется два массива размерностью (N+1), где величина N зависит от времени пробега волны по линии и выбранного шага (h) расчета N= t₁₂/h.

          В общем случае шаг численного решения h определяется необходимой точностью решения узловых уравнений, временем пробега волны по линии, частотным спектром воздействующих на схему импульсов напряжения и видом нагрузки в узлах – наличием активных линейных или нелинейных элементов, а также элементов, запасающих энергию (емкостей или индуктивностей).

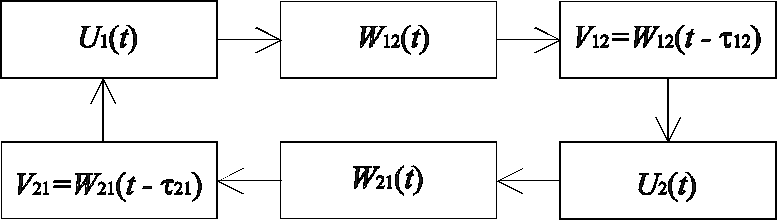
а)

б)

          Рис. 2. Блок-схема программы (а) и алгоритм движения волн (б) для

          исследования волновых процессов  в схеме с двумя узлами 1 и 2,

         соединенными  линией с распределенными параметрами.

          Современное развитие вычислительной техники позволяет не подходить строго к оптимальному выбору шага решения с точки зрения экономии машинного времени и обеспечения необходимой точности расчета, поэтому для исследования волновых процессов при воздействии на схему импульсов напряжения с достаточно крутыми фронтами и варьировании параметров R, L и C в реальных диапазонах их изменения согласно вычислительным экспериментам достаточно выбрать шаг расчета  в диапазоне 0,01…0,1 мкс. При этом следует отметить, что шаг решения должен укладываться целое число раз во времени пробега волны по линии.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

          При выполнении лабораторной работы каждому студенту выдается в соответствии с табл.П2 вариант расчетной схемы, для которой на базе  разработанной математической модели, реализованной применительно к ПЭВМ, необходимо провести анализ волнового процесса при воздействии на схему            (табл.П.3) импульса напряжения заданной формы (табл.П.4).