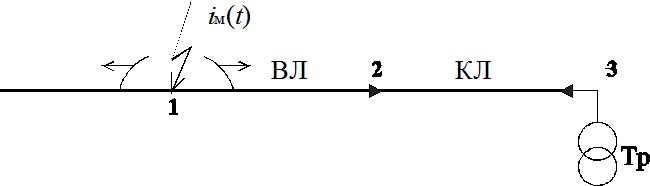
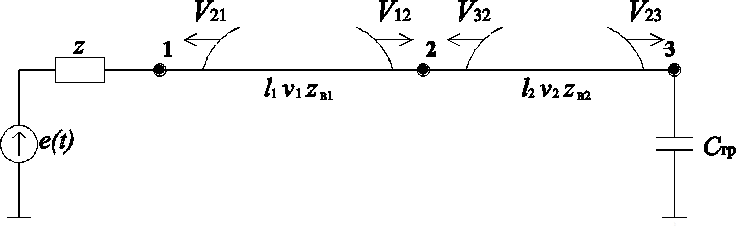
Электротехника \ Физико-математические основы электроэнергетики

Исследование переходных процессов в схемах с распределенными параметрами, страница 2

В качестве примера составим математическую модель, позволяющую исследовать электромагнитные переходные процессы, возникающие в схеме при ударе молнии в линию в непосредственной близости от кабельной вставки, в конце которой подключен ненагруженный трансформатор. На рис.3 представлены исходная  и расчетная схемы замещения, содержащая три узла и связывающие эти узлы отрезки воздушной и кабельной линий. В  схеме приняты следующие исходные данные:

e(t)   -  воздействующий импульс напряжения конечной длительности,

l1= 1500 м  и l2= 600 м  - соответственно, длины воздушной и кабельной линии,

n1= 300 м/мкс и n2= 150 м/мкс  - скорости распространения электромагнитной волны по воздушной и кабельной линии,

Z = ZВ1= 400 Ом  и  ZВ2 = 40 Ом   -  волновые сопротивления ВЛ и КЛ,

Стр = 2000 пФ   -  входная емкость трансформатора на частоте грозового импульса напряжения.

          Исходные уравнения для узлов записываются в виде:

узел 1:

                              V21(t) = u1(t) + i21(t) ZВ1  ,

                              u1(t)  = e(t) – i(t) Z ,                                                            (4)

                                 i(t)  = – i21(t),                                                          

                             W12(t) = 2u1(t) – V21(t).   

а)

б)

Рис. 3. Исходная  (а) и расчетная (б) схемы замещения  для анализа

             волновых процессов в схеме с распределенными параметрами

узел 2:

                               V12(t) = u2(t) + i12(t) ZВ1  ,

                               V32(t) = u2(t) + i32(t) ZВ2  ,

                                 i12(t) = – i32(t),                                                                            (5)

                               W21(t) = 2×u2(t) – V12(t) ,   

                               W23(t) = 2×u2(t) – V32(t) .   

узел 3:

                               V23(t) = u3(t) + i23(t) ZВ2  ,

                                 i23(t) = Стр du3(t)/dt ,                                                                   (6)

                              W32(t) = 2u3(t) – V23(t) .             

          При неучете потерь в воздушной и кабельной линии приходящие в узлы волны определятся как:

                                V12(t) = W12(t–t12),

 V21(t) = W21(t–t21) ,                                                  

                                V23(t) = W23(t–t23),                                             (7)

 V32(t) = W32(t–t32),                         

где t12  и  t23  -  времена пробега волны по воздушной и кабельной линии, соответственно.

          Для определения u1(t), u2(t) и u3(t) системы уравнений (4)…(6) целесообразно переписать в виде:  

 


                     u1(t) = [V21(t) Z + e(t) ZВ1]/(Z + ZВ1) ,           

                     u2(t) = [V12(t) ZВ2 + V32(t) ZВ1]/(ZВ1 + ZВ2) ,

                     du3(t)/dt = [V23(t) – U3(t)]/Cтр/ZВ2 ,                                                           (8)

                     W12(t) = 2u1(t) – V21(t) ,    W21(t) = 2u2(t) – V12(t) ,   

                     W23(t) = 2u2(t) – V32(t) ,    W32(t) = 2u3(t) – V23(t) .             

          При использовании для численного интегрирования обыкновенного дифференциального уравнения  dy(t)/dt = f [y(t), t], например, неявного метода трапеций, решение уравнения на (k+1)-м шаге интегрирования  (t= k×h) запишется в виде

                          y[(k+1)h] = y(kh) + 0,5×h [f(yk+1,tk+1) + f(yk,tk)] .                              (9)

Соответственно, напряжение в узле 3 на (k+1)-ом шаге интегрирования можно определить как

             u3(k+1) = [u3(k) + (V23(k) +V23(k+1) – u3(k))×h/2/ZВ2/Стр]/(1+ h/2/ZВ2/Cтр).            (10)

          Таким образом, расчет переходного процесса в исследуемой схеме сводится к решению системы уравнений (8) при известных значениях волн, приходящих в узлы схемы, определению волн, отраженных от узлов и имитации движения обобщенных волн по линиям в соответствии с  волновыми уравнениями (7).

          Для реализации этой модели может быть использована какая-либо из систем инженерных расчетов: MATLAB, Mathcad, EXCEL и др.  Ниже приведены примеры использования для реализации рассмотренного алгоритма систем MATLAB и EXCEL

 Пример реализации математической модели в системе MATLAB 

Программа расчета переходных процессов в схеме, приведенной на рис.3, при использовании метода  бегущих волн имеет вид:

% Исходные данные

tr=40e-6;                                               - время расчета  переходного процесса                      

h=0.1e-6;                                               - шаг расчета       

L1=1500;L2=600;                                - длина ВЛ и КЛ         

v1=300.e6;v2=150.e6;                          - скорости распр. волн по ВЛ и КЛ             

Z1=400;Z2=40;                                     - волновые сопротивления ВЛ и КЛ         

C=2e-9;                                               - входная емкость трансформатора          

U0=1;                                                  - амплитуда воздействующей волны 

ti=2e-6;                                               - длительность срезанного импульса

U3k=0;                                                - начальное значение U3(t)   

nt=tr/h;                                                - количество циклов по времени  

% Начальные значения массивов напряжений и времени

UM1=0;UM2=0;UM3=0;tm=0;

% Формирование размерности для массивов волн

N1=round(1+L1/v1/h);

N2=round(1+L2/v2/h);

% Формирование начальных (нулевых) массивов волн

V12=zeros(1,N1);

V21=zeros(1,N1);

V23=zeros(1,N2);

V32=zeros(1,N2);

% Расчет волнового процесса (цикл по времени)

for k=1:nt

   t=k*h;

%   if(t<=ti)                                                                   

%      e=2*U0-2*U0*(ti-t)/ti;   

%   else                                                 - срезанный импульс  

%      e=0;

%      end

e=2*U0;                                                - прямоугольный импульс

      % Сдвиг волн на шаге расчета

      for i=N1:-1:2

         V12(i)=V12(i-1);

         V21(i)=V21(i-1);

      end

      for i=N2:-1:2

         V23(i)=V23(i-1);

         V32(i)=V32(i-1);

      end

      % Вычисление значений напряжения в узлах

      U1=(V21(N1)+e)/2;

      U2=(V12(N1)*Z2+V32(N2)*Z1)/(Z1+Z2);

      U3=(U3k+h*(V23(N2)+V23(N2-1)-U3k)/2/Z2/C)/(1+h/2/Z2/C);

      U3k=U3;

      % Формирование массивов напряжений и времени

      UM1=[UM1 U1];

      UM2=[UM2 U2];

      UM3=[UM3 U3];

      tm=[tm t*1.e6];

      % Вычисление отраженных (падающих) волн

      V12(1)=2*U1-V21(N1);

Скачать файл