Расчетное задание № 1.
Исследование переходных процессов
в цепях с сосредоточенными параметрами.
· Для заданной схемы с сосредоточенными параметрами (контур второго порядка) составить уравнения, описывающие процессы в схеме.
· Рассчитать переходные процессы в контуре (напряжение на емкости, ток в индуктивности) при включении постоянной э.д.с. с помощью численных методов интегрирования дифференциальных уравнений. Подобрать величины активных сопротивлений таким образом, чтобы переходный процесс в контурах имел колебательный характер.
· Оценить максимальные значения напряжений и токов в переходном процессе по инженерной методике и сравнить с результатами расчета численным методом.
· Рассчитать переходные процессы в контуре при включении
переменной э.д.с. ![]() при углах включения
при углах включения ![]() и
и ![]() .
.
· Составить отчет, проанализировать полученные результаты.
Для анализа переходных процессов в схеме с сосредоточенными параметрами необходимо записать уравнения, описывающие процессы в схеме. При современном уровне развития вычислительной техники дифференциальные уравнения при заданных начальных условиях можно решить, используя численные методы расчета. Для этого необходимо записать полученные уравнения в форме Коши:
![]()
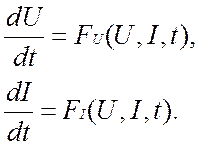 (1.1)
(1.1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() R
L
R
L
![]()
![]()
![]()
![]() e(t)
C
e(t)
C
Рис.1.1. Пример расчетной схемы.
Например, переходные процессы в контуре R,L,C, изображенном на рис. 1.1, описываются следующей системой уравнений:
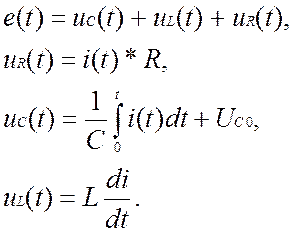 (1.2)
(1.2)
Уравнения (1.2) в форме Коши будут иметь вид:
![]()
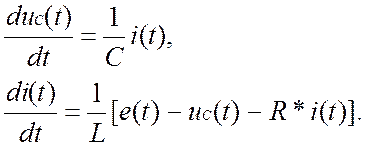 (1.3)
(1.3)
Решить систему уравнений, описывающую процессы в заданной схеме, можно при помощи одной из систем инженерных и научных расчетов MathCAD (MathCAD 7/0 PRO) или MATLAB (MATrix LABarotatory), в состав которых входят в том числе функции численного интегрирования системы обыкновенных дифференциальных уравнений. Рассмотрим примеры решения системы уравнений (1.3) в обеих этих системах.
В МathCAD введен ряд функций [2], дающих решения для систем обыкновенных дифференциальных уравнений. Остановимся на одной из них:
rkfixed(X,T1,T2,n,D) - возвращает матрицу решений методом Рунге-Кутта
системы обыкновенных дифференциальных
уравнений с начальными условиями в векторе X,
правые части которых записаны в символьном
векторе D,на интервале от T1 до T2 при
фиксированном количестве шаговрасчета n.
Решение системы дифференциальных уравнений методом Рунге-Кутта с фиксированным шагом.
Исходные данные:
R:=100 L:=1 C:=10-6
e(t):=1 To:=0 Tmax:=0.1
Решение:
![]() - параметр системы
- параметр системы
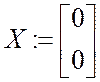 - вектор начальных
условий
- вектор начальных
условий
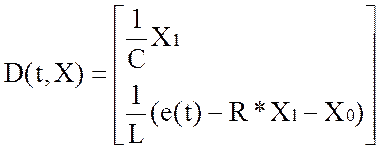 - система
дифференциальных уравнений
- система
дифференциальных уравнений
![]() - задание решения
- задание решения
n:=0…1000 - номера шагов расчета, выводимых на график
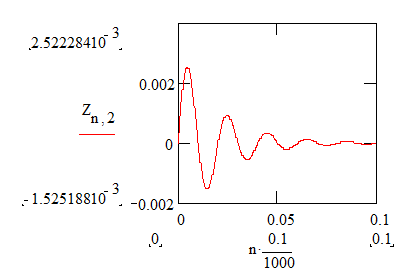
График тока во времени (t=Tma.x./N)
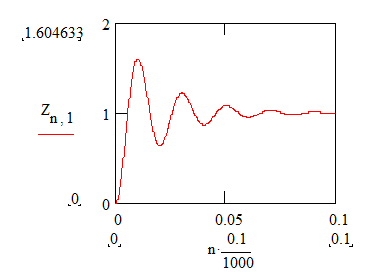
График изменения напряжения во времени
Рис.1.2. Решение системы дифференциальных уравнений с применением функции
rkfixed ( включение схемы на постоянную э.д.с.)
Рис.1.2. иллюстрирует технику решения системы из двух дифференциальных уравнений (1.3) и построение расчетных кривых изменения тока и напряжения во времени. В расчете введены следующие обозначения:
X - вектор начальных условий (UС = 0, i0 = 0 ),
X0 - обозначение переменной, производная которой вычисляется в первом
уравнении системы (1.3),
X1 - обозначение переменной, производная которой вычисляется во втором
уравнении системы (1.3),
D(t,X) - матрица, вычисления правых частей дифференциальных уравнений,
T0 и Tmax – время начала и конца расчета.
Численное интегрирование системы обыкновенных дифференциальных уравнений (1.3) при использовании системы Matlab осуществляется следующим образом: уравнения (1.3) записываются в виде отдельной функции (rlc.m), расположенной в основной (головной) программе ( Main.m) и затем с помощью встроенной процедуры осуществляется решение дифференциальных уравнений одним из численных методов ( например методом трапеций при использовании стандартной процедуры - ode23t ).
Пример основной программы Main.m
global R L C w
R=100; L=0.1; C=1.e-6; % задание параметров схемы
w=100*pi; % задание частоты источника
t0=0; % начальное время расчета
tf=0.1; % конечное время расчета
y0=[0 0]; % вектор начальных условий (UC=0,i0=0)
ts=[t0 tf]; % диапазон времени расчета от t0 до tf
[t,y]=ode23t('rlc',ts,y0); % решение системы уравнений (1.3)
subplot(211),plot(t,y(:,1),'red'),grid; % построение графика i(t)
title('Ток в контуре') % название графика
subplot(212),plot(t,y(:,2),'green'),grid; % построение графика U(t)
title('Напряжение на конденсаторе') % название графика
Пример подпрограммы-функции rlc.m
function yp=rlc(t,y)
global R L C w
e=1; % включение постоянной э.д.с.
%e=sin(w*t) % включение синусоидальной э.д.с.
%e=sin(w*t+pi/2) % включение синусоидальной э.д.с.
yp=[e/l-y(1)*r/l-y(2)/l; y(1)/c]; % реализация правых частей системы (1.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.