На рис. 1.3 и 1.4 приведены полученные в системе Matlab расчетные кривые изменения тока в схеме и напряжения на емкости при включении исследуемого контура на постоянную и переменную э.д.с.
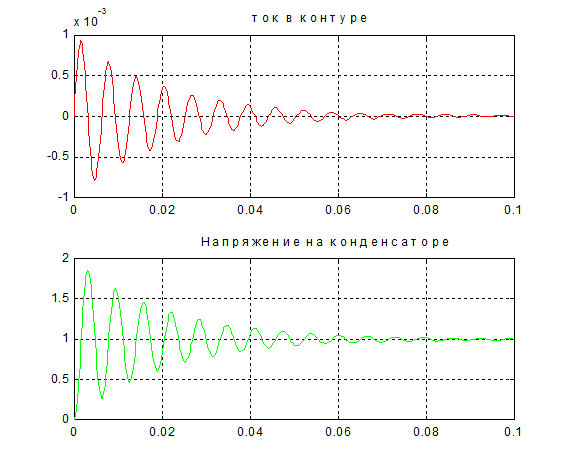
Рис.1.3 Расчетные кривые при включении схемы на постоянную э.д.с.
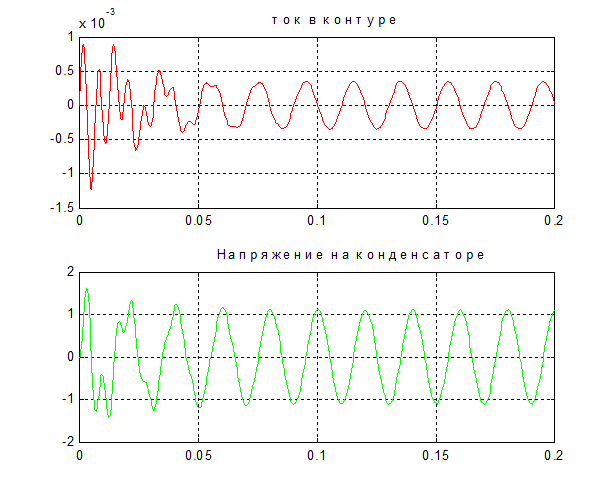
Рис.1.4 Расчетные кривые при включении схемы на переменную э.д.с.
Часто исследователя интересует не форма кривой напряжения или тока, а лишь значения их максимальных величин в переходном процессе Umax и Imax. Выведем формулы для определения Umax и Imax с помощью простой инженерной методики.
Как известно [4], после затухания переходного процесса источник э.д.с. создает установившийся (вынужденный) режим. При переходе цепи от одного установившегося состояния к другому на установившиеся (вынужденные) составляющие напряжения и тока, которые наступили как бы сразу после коммутации, накладываются свободные (переходные) составляющие, которые существуют только в переходном процессе. Следовательно, напряжения и токи в линейных цепях в любой момент времени можно представить следующим образом:
![]()
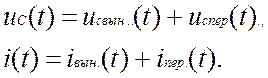 (1.4)
(1.4)
Вынужденные составляющие тока и напряжения в контуре,
приведенном на рис.1.1, при включении постоянной э.д.с. e(t)=Eбудут равны Iвын.=0, Uвын.=Е.При включении переменной э.д.с. ![]() вынужденные составляющие тока и
напряжения будут синусоидальны и равны
вынужденные составляющие тока и
напряжения будут синусоидальны и равны
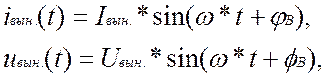 (1.5)
(1.5)
где
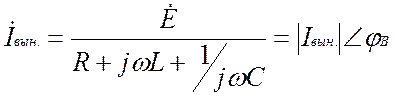 , (1.6)
, (1.6)
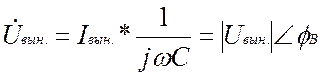 .
.
Переходный процесс обусловлен несоответствием
значений токов и напряжений в контуре до и после коммутации. Электромагнитная
энергия, затрачиваемая на переходный процесс, определяется разницей токов в
индуктивности до и после коммутации 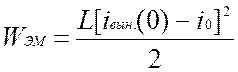 . Электростатическая энергия, затрачиваемая на
переходный процесс, определяется разницей напряжений на емкости до и после
коммутации
. Электростатическая энергия, затрачиваемая на
переходный процесс, определяется разницей напряжений на емкости до и после
коммутации
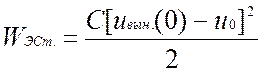 . В процессе колебаний вся энергия, расходуемая на
переходный процесс, W=WЭМ+WЭСт. может быть
сосредоточена либо в индуктивности (при этом ток в индуктивности будем
максимальным), либо в емкости ( при этом максимальным будет напряжение на
емкости).
. В процессе колебаний вся энергия, расходуемая на
переходный процесс, W=WЭМ+WЭСт. может быть
сосредоточена либо в индуктивности (при этом ток в индуктивности будем
максимальным), либо в емкости ( при этом максимальным будет напряжение на
емкости).
В соответствии с законом сохранения энергии максимальные амплитудные значения переходной составляющей напряжения на емкости Uпер и тока в индуктивности Iпер. определиться как
![]() ,
,
![]() .
(1.7)
.
(1.7)
где 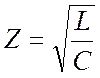 -
характеристическое сопротивление контура.
-
характеристическое сопротивление контура.
Дифференциальные уравнения, описывающие процессы в контуре для переходных составляющих тока и напряжения, могут быть записаны аналогично уравнениям (1.3) при отсутствии э.д.с. и после преобразования иметь вид:
![]()
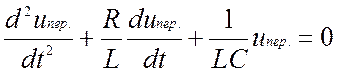 ,
,
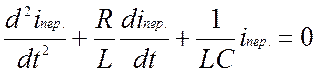 .
(1.8)
.
(1.8)
Характер изменения переходных составляющих токов и напряжений зависит только от параметров контура R-L-C, иначе говоря, от вида корней характеристического уравнения
![]() .
(1.9)
.
(1.9)
В (1.9) приняты следующие обозначения: 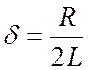 ,
, 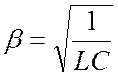 .
.
Корни характеристического уравнения (1.9) определяются равенством
![]() . (1.10)
. (1.10)
Переходные составляющие тока и
напряжения iпер. и uпер. будут иметь
апериодический характер, в том случае, если корни характеристического уравнения
действительные (при ![]() ), или колебательный
характер, если корни мнимые (при
), или колебательный
характер, если корни мнимые (при ![]() ). Можно подобрать
величину активного сопротивления в контуре таким образом, чтобы переходный
процесс в нем имел колебательный характер. В этом случае изменения iпер.
и uпер. представляются затухающими синусоидальными функциями
с угловой частотой колебаний контура
). Можно подобрать
величину активного сопротивления в контуре таким образом, чтобы переходный
процесс в нем имел колебательный характер. В этом случае изменения iпер.
и uпер. представляются затухающими синусоидальными функциями
с угловой частотой колебаний контура ![]() и
коэффициентом затухания
и
коэффициентом затухания ![]() .
.
![]()
![]() ,
, 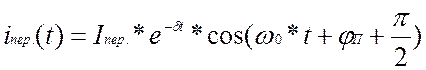 , (1.11)
, (1.11)
где
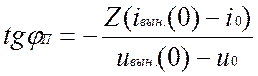 .
.
В соответствии с (1.4) напряжение на емкости и ток в любой момент времени переходного процесса при включении постоянной э.д.с. можно определить по выражениям:
![]()
![]() ,
,
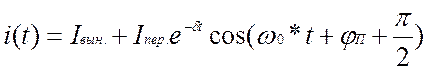 , (1.12)
, (1.12)
при включении переменной э.д.с.:
![]()
![]() ,
,
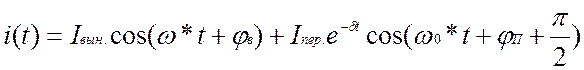 . (1.13)
. (1.13)
Наибольшие в течение переходного процесса значения
напряжений и токов в контуре совпадают по времени с максимумами iпер.
и uпер . При этом максимум uпер
соответствует времени 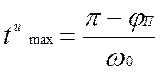 , максимум iпер.
– времени
, максимум iпер.
– времени 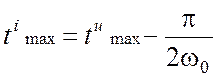 .
.
Введем следующие обозначения:
![]()
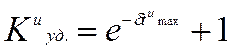 - ударный коэффициент перенапряжений,
- ударный коэффициент перенапряжений,
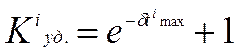 -
ударный коэффициент сверхтоков.
-
ударный коэффициент сверхтоков.
С учетом этих обозначений максимальные в переходном процессе напряжения и токи при включении постоянной э.д.с. можно найти по формулам:
![]()
![]() .
(1.14)
.
(1.14)
В контуре с переменной э.д.с. максимальные в переходном процессе напряжения и токи можно определить из следующих соображений:
·
Если частота собственных колебаний
контура много больше синхронной частоты (![]() ),
можно считать, что вынужденные составляющие напряжения и тока практически не
изменяются в течение всего переходного процесса и равны uвын.(0) и iвын.(0). При этом Umax и Imax равны
),
можно считать, что вынужденные составляющие напряжения и тока практически не
изменяются в течение всего переходного процесса и равны uвын.(0) и iвын.(0). При этом Umax и Imax равны
![]()
![]() . (1.15)
. (1.15)
·
Если частота собственных колебаний
контура сопоставима с синхронной частотой (1,5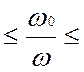 3),
максимально возможные Umax и Imax будут в
случае совпадения максимумов вынужденных и переходных составляющих напряжений и
токов. При этом Umax и Imax с
запасом можно определить по выражениям (1.14), Uвын. и Iвын.в которых равны амплитудным значениям вынужденных
составляющих напряжения и тока.
3),
максимально возможные Umax и Imax будут в
случае совпадения максимумов вынужденных и переходных составляющих напряжений и
токов. При этом Umax и Imax с
запасом можно определить по выражениям (1.14), Uвын. и Iвын.в которых равны амплитудным значениям вынужденных
составляющих напряжения и тока.
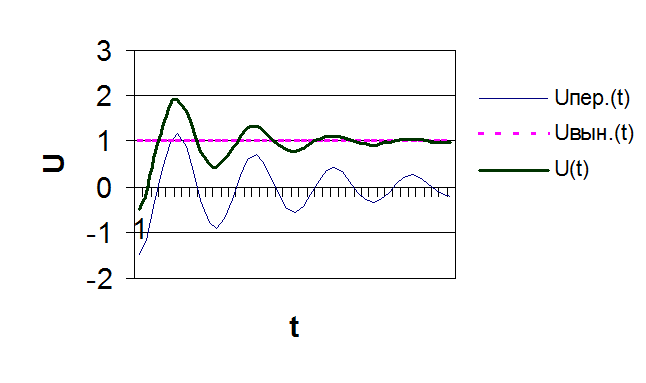
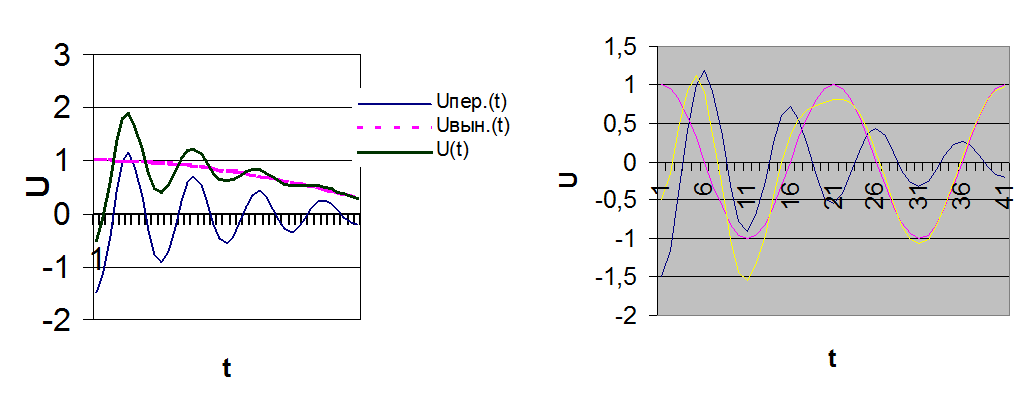
На рис. 1.5 в качестве иллюстрации приведены кривые изменения всех составляющих переходных процессов в контуре при включении постоянной (а) и переменной э.д.с. (б и в).
 |
б) ![]() в)
в)
![]()
Рис. 1.5 Кривые, иллюстрирующие изменения всех составляющих переходных процессов в контуре при включении постоянной (а) и переменной э.д.с. (б и в).
1. Перенапряжения в электрических системах и защита от них: Учебник для вузов/ В.В. Базуткин, К.П. Кадомская, М.В. Костенко, Ю.А. Михайлов.-СП.:Энергоатомиздат, Санкт-Петербург. отделение.1995.-320 с., ил.
2. В.П. Дьяконов, И.В. Абраменкова- MathCAD 7.0 в математике, физике и в Internet.-м.:”Нолидж”, 1998.-352 с., ил.
3. Потемкин В.Г.-Система MATLAB. Справочное пособие.-М.-ДИАЛОГ-МИФИ, 1998 –350 с.
4. Основы теории цепей: Учебник для вузов/ Г.В. Зевеке, П.А. Ионкин,
А.В. Нетушил, С.В. Страхов.- 5-е изд.,перераб.-М.:Энергоатомиздат,1989.
-528 с.: ил.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.