













6. Уравнения плоскости и прямой
6.1. Геометрические способы задания прямой и плоскости
Приведем некоторые сведения из школьного курса геометрии, касающиеся прямой и плоскости. Известно, что математические утверждения делятся на аксиомы и теоремы. Аксиомы принимаются без доказательства, а теоремы являются логическими следствиями из системы аксиом. Не будем разделять аксиомы и теоремы, объединяя их общим термином «утверждения».
Утверждение 1. Через любые две точки проходит прямая, и притом только одна.
Утверждение 2. Через любую точку, не лежащую на прямой, проходит другая прямая, параллельная данной, и притом только одна.
Утверждение 3. Через любые три точки, не лежащие на прямой, проходит плоскость, и притом только одна.
Утверждение 4. Через две пересекающиеся прямые проходит плоскость и притом только одна.
Утверждение 5. Через любую точку пространства проходит прямая, перпендикулярная плоскости и притом только одна.
Утверждение 6. Если две прямые перпендикулярны к плоскости, то они параллельны.
Опираясь на утверждения 1-6, и учитывая, что любой отрезок (направленный или ненаправленный) полностью определяет прямую, частью которой он является, перечислим некоторые способы задания плоскости.
|
•
• |
Способ 1. Прямая однозначно определена, если заданы две точки, через которые она проходит |
|
• • |
Способ 1. Прямая однозначно определена, если заданы точка, через которую она проходит, и отрезок, параллельный прямой и не лежащий на ней. |
|
|
Способ 1. Плоскость однозначно определена, если указана точка, лежащая в этой плоскости, и вектор (направленный отрезок), перпендикулярный этой плоскости. |
|
• |
Способ 2. Плоскость однозначно определена, если указаны три точки, лежащие в этой плоскости. |
|
|
Способ 3. Плоскость однозначно определена, если указаны точка, лежащая в этой плоскости, и два неколлинеарных вектора, параллельных этой плоскости. |
6.2.Уравнения плоскости
Выберем в пространстве декартову прямоугольную систему
координат с базисом ![]() . В некоторых случаях,
вместо термина «система координат» удобнее применять термин «репер»
. В некоторых случаях,
вместо термина «система координат» удобнее применять термин «репер»
Определение 6.1. Репером или системой координат в
пространстве называют
упорядоченный набор ![]() , состоящий из
зафиксированной точки пространства
, состоящий из
зафиксированной точки пространства ![]() , называемой началом
координат, и базиса
, называемой началом
координат, и базиса ![]() пространства.
пространства.
Каждая точка ![]() определяет
вектор
определяет
вектор ![]() =
=![]() ,
приложенный к началу координат. Координатами вектора
,
приложенный к началу координат. Координатами вектора ![]() =
=![]() являются координаты точки
являются координаты точки ![]() . Вектор
. Вектор ![]() называют
радиус-вектором точки
называют
радиус-вектором точки ![]() . Любая пара точек
. Любая пара точек
![]() и
и ![]() определяет
вектор
определяет
вектор ![]() =
=![]() ,
координатами которого являются разности координат точек
,
координатами которого являются разности координат точек ![]() и
и
![]() :
: ![]() =
=![]() .
.
Пусть![]()
![]() =
=![]() -
точка и вектор в этом пространстве. Они однозначно определяют плоскость
-
точка и вектор в этом пространстве. Они однозначно определяют плоскость ![]() , проходящую через точку
, проходящую через точку ![]() и перпендикулярную вектору
и перпендикулярную вектору ![]() [1].
Пусть также
[1].
Пусть также ![]() - любая точка, лежащая в плоскости
- любая точка, лежащая в плоскости ![]() , не совпадающая с
, не совпадающая с ![]() . Отрезок
. Отрезок ![]() ,
а значит и вектор
,
а значит и вектор ![]() перпендикулярны вектору
перпендикулярны вектору ![]() . Следовательно, скалярное
произведение векторов
. Следовательно, скалярное
произведение векторов ![]() и
и ![]() равно
нулю:
равно
нулю:
![]() =
=![]() =0.
=0.
Переобозначим: ![]() .
Тогда координаты любой точки, лежащей в плоскости
.
Тогда координаты любой точки, лежащей в плоскости ![]() , удовлетворяют
равенству:
, удовлетворяют
равенству:
|
|
(6.1) |
В то же время, если точка не лежит в плоскости ![]() , то ее координаты не удовлетворяют
равенству (6.1). Равенство (6.1) называют уравнением плоскости,
проходящей через заданную точку, перпендикулярно заданному вектору.
, то ее координаты не удовлетворяют
равенству (6.1). Равенство (6.1) называют уравнением плоскости,
проходящей через заданную точку, перпендикулярно заданному вектору.
Раскроем скобки в уравнении (6.1) и обозначим число ![]() . Равенство (6.1) примет вид:
. Равенство (6.1) примет вид:
|
|
(6.2) |
которое называют общим уравнение плоскости.
Геометрический смысл коэффициентов ![]() в уравнении (6.2) очевиден: то
координаты известного вектора нормали к плоскости
в уравнении (6.2) очевиден: то
координаты известного вектора нормали к плоскости ![]() =(
=(![]() ). Выясним геометрический смысл
свободного члена уравнения, числа
). Выясним геометрический смысл
свободного члена уравнения, числа ![]() . Найдем
. Найдем ![]() =
=![]() ,
то есть вектор сонаправленный
,
то есть вектор сонаправленный ![]() и имеющий
единичную длину (см. стр ).
и имеющий
единичную длину (см. стр ). ![]() =(
=(![]() ), причем
), причем ![]() =1
или
=1
или ![]() . Чтобы нормировать вектор
. Чтобы нормировать вектор ![]() , надо его координаты (
, надо его координаты (![]() ), разделить на его длину, то есть на
число
), разделить на его длину, то есть на
число ![]() . Получим:
. Получим:
![]() =(
=(![]() )=
)=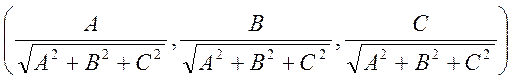 .
.
Разделим уравнение (6.2) на длину вектора ![]() :
:
|
|
(6.3) |
где
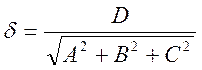 . Уравнение (6.3) называют нормированным
уравнением плоскости.
. Уравнение (6.3) называют нормированным
уравнением плоскости.
Рассмотрим вектор ![]() =(
=(![]() ). При любом
). При любом ![]() он
коллинеарен вектору
он
коллинеарен вектору ![]() , его начало совпадает с
началом координат. Подберем
, его начало совпадает с
началом координат. Подберем ![]() таким, чтобы
конец вектора
таким, чтобы
конец вектора ![]() лежал на плоскости. Тогда
лежал на плоскости. Тогда ![]() - это расстояние от начала координат
до плоскости. Концом искомого вектора является точка, координаты которой
удовлетворяют уравнению (6.3):
- это расстояние от начала координат
до плоскости. Концом искомого вектора является точка, координаты которой
удовлетворяют уравнению (6.3):
![]()
![]()
![]() .
.
Обозначим
расстояние от начала координат до плоскости ![]() .
Тогда
.
Тогда ![]() =
= ![]() при
при
![]() , то есть:
, то есть: ![]()
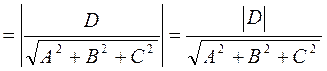 .
.
|
|
(6.4) |
Итак, абсолютная величина свободного члена в общем уравнении плоскости есть произведение расстояния от начала координат до плоскости на длину ее нормального вектора. Если уравнение плоскости нормировано, то абсолютная величина свободного члена есть расстояние от начала координат до плоскости.
Пусть заданы три точки![]() ,
,
![]() и
и ![]() .Эти
точки однозначно определяют плоскость
.Эти
точки однозначно определяют плоскость![]() , в которой они
лежат. Пусть также
, в которой они
лежат. Пусть также ![]() - любая точка, лежащая в плоскости
- любая точка, лежащая в плоскости
![]() , не совпадающая ни с одной из точек
, не совпадающая ни с одной из точек ![]() ,
, ![]() или
или
![]() . Векторы
. Векторы ![]() ,
,
![]() и
и ![]() компланарны.
Следовательно, их смешанное произведение (
компланарны.
Следовательно, их смешанное произведение (![]()
![]()
![]() )
равно нулю (см. стр. ), то есть справедливо равенство:
)
равно нулю (см. стр. ), то есть справедливо равенство:
|
|
(6.5) |
которое называют уравнением плоскости, проходящей через три заданные точки.
Пользуясь свойствами определителей, представим определитель в равенстве (6.5) в виде суммы двух определителей:
![]() =
=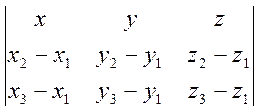 +
+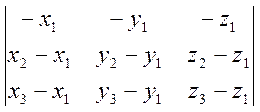 .
.
Первой строкой определителя ![]() являются
переменные
являются
переменные ![]() ,
, ![]() и
и
![]() . Разложив его по первой строке,
получим:
. Разложив его по первой строке,
получим:
![]() =
=![]() -
-
-![]() +
+
+![]() =
=![]() ,
,
где
![]() - коэффициенты перед переменными,
полученные в результате вычислений. Обозначим число, полученное в результате
вычисления определителя
- коэффициенты перед переменными,
полученные в результате вычислений. Обозначим число, полученное в результате
вычисления определителя ![]() через
через ![]() .
.
После этих преобразований, уравнение плоскости,
проходящей через три заданные точки, примет вид общего уравнения плоскости: ![]() .
.
Плоскость однозначно определена, если указаны точка,
лежащая в этой плоскости, и два неколлинеарных вектора, параллельных этой
плоскости. Пусть ![]() - точка, лежащая в
плоскости
- точка, лежащая в
плоскости ![]() ,
, ![]() =
=![]() и
и ![]() =
=![]() - два неколлинеарных друг другу
вектора, причем оба параллельны плоскости
- два неколлинеарных друг другу
вектора, причем оба параллельны плоскости ![]() .
Векторное произведение векторов
.
Векторное произведение векторов ![]() и
и ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.