ТФНП, интеграл по фигуре, тройной интеграл, вопросы и тесты

Лекция 1. ТФНП

1.  , ,  – ?

2.  Привести пример несвязного множества (м. геометрическую интерпретацию).

3.  Привести пример функции, точки разрыва которой образуют поверхность.

4.  Что нужно указать, для того чтобы доказать по определению, что функция нескольких переменных имеет предел в некоторой точке (общий алгоритм).

5.  Известно, что частные производные функции в точке  непрерывны. Следует ли из этого, что функция непрерывна в точке ?

Лекция 3. Интеграл по фигуре

1.  Обосновать (или опровергнуть) необходимость стремления  помимо  в определении интеграла по фигуре .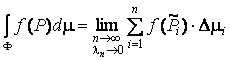

2.  Вычислить , если , где , .

3.  Вспомнить (сформулировать) аналог теоремы о среднем для функции одной переменной.

4.  Чем являются значения  и  для множества значений функции (7 п., 3 св.).

5.  Какие характеристики позволяет вычислить интеграл по фигуре (скалярные, векторные).

Лекция 5. Тройной интеграл

1.  Сформулировать замечания к случаю перехода к ССК, аналогично рассмотренным заменам.

Лекция 7. Криволинейный и поверхностный интеграл первого рода.
Механические приложения кратных интегралов

1.  Каким образом получено уравнение касательной плоскости и координаты нормального вектора из выведенных формул в ТФНП?

2.  Записать формулу, позволяющую вычислить поверхностный интеграл I рода для функции .

3.  Записать параметризацию поверхности .

4.  Каким образом при переходе  получили ?

5.  Вычислить знаменатель  в последнем примере.