Уравнения плоскости и прямой, страница 3

При переходе к трехмерному пространству с заданной декартовой прямоугольной системой координат происходит естественное обобщение уравнений прямой на плоскости на трехмерный случай. Запишем основные виды уравнений прямой  в трехмерном пространстве,

Название уравнения	Вид уравнения	Геометрический смысл чисел, входящих в уравнение
Уравнение прямой , проходящей через две заданные точки		, - координаты двух заданных точек, через которые проходит прямая .
Каноническое уравнение прямой		- координаты заданной точки прямой ; - координаты направляющего вектора.
Параметрическое уравнение прямой		Геометрический смысл  и тот же самый, что и в каноническом уравнении, - свободная переменная, параметр.

Обратим внимание на то, что все, приведенные в таблице, виды уравнений прямой могут быть представлены как системы уравнений двух плоскостей.

Например, уравнение прямой, проходящей через две заданные точки:

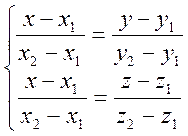
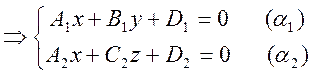
В уравнении плоскости : , , ; координата отсутствует, следовательно, плоскость  или, что то же самое, ‌‌ ‌ . Аналогично для плоскости :

или ‌ ‌ ; , , .

Также и остальные уравнения прямой можно представить как системы уравнений двух плоскостей, параллельных координатным плоскостям. В общем случае плоскости , линией пересечения которых является прямая , могут быть расположены произвольно относительно системы координат. Систему уравнений двух плоскостей называют общим уравнением прямой. Общее уравнение прямой - это уравнение линии пересечения данных плоскостей:

В заключение приведем векторное уравнение прямой:

где =- радиус-вектор произвольной точки, лежащей на прямой, = - радиус-вектор известной, фиксированной точки этой прямой,  - направляющий вектор прямой. Векторное уравнение прямой, лежащей в плоскости, имеет вид (6.  ), но все векторы, входящие в него, имеют лишь по две координаты.

6.5. Преобразование координат

Рассматривая уравнения плоскости и прямой, мы подчеркивали их связь с выбранным репером. В этом разделе рассмотрим, как меняются эти уравнения при переходе от одного репера к другому.

Будем рассматривать геометрические пространства с ортонормированными базисами, то есть базисами состоящими из единичных векторов, попарно перпендикулярных друг другу. Реперы с такими базисами могу отличаться друг от друга (а) точкой приложения базиса, (б) направлениями базисных векторов.

Пусть точки приложения базиса (,) – точки и . Точка имеет радиусы-векторы  в репере ,  и в репере . Точка  в репере  имеет радиус-вектор .

·	Так как =+, то формулы перехода от одного репера к другому имеют вид:  или ,          (6.19) где  -координаты точки  в репере , - координаты той же точки в репере , - координаты точки  (нового начала координат) в репере .

Равенства (6.19) можно записать более компактно:

где  - радиус вектор точки  в репере ,  - радиус вектор той же точки в репере ,  - радиус-вектор «нового» начала координат в «старом» репере.

·	Пусть векторы и  в репере имеет координаты =(), =(), то есть =, =. Радиус-вектор точки в реперах  и  :  = =+= ==.

Следовательно, имеем:

,

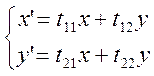или в матричной форме:

где  - столбец координат точки в репере , = 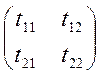матрица перехода от репера  к реперу , столбцами которой являются координаты векторов  и  в репере , = - столбец координат точки  в репере .

Если найти матрицу , обратную матрице , то можно выразить  через :

Столбцы матрицы  - это координаты векторов  и  в репере .

В случае трехмерного геометрического пространства будут справедливы равенства (6.21 ) и (6.22), но векторы  и  будут содержать по три координаты, а матрицы  и  иметь три строки и три столбца.

Таким образом, переход от одного репера к другому удобно выполнять в два шага:

Шаг 1.  Выполнить перенос начала координат, пользуясь формулой: .

Шаг 2. Выполнить поворот осей координат, пользуясь формулой:.

Пример. Прямая  задана своим общим уравнением:

:  .

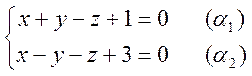Записать уравнение этой прямой в системе координат, начало которой является какая-либо точка прямой ,  сонаправлена вектору нормали плоскости , ось  проходит по прямой , базис является левой тройкой векторов.

Решение.

1.Найдем какую-либо точку лежащую на прямой  и перенесем в нее начало координат. Пусть

.

Новое начало координат: . Пользуясь формулами 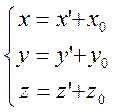, запишем уравнение прямой в системе координат с началом в точке :

.

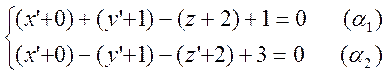
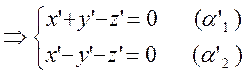2. Найдем векторы, сонаправленные новым координатным осям, и, нормировав их, получим новый базис.

Вектор нормали плоскости :  . Напомним, что координаты вектора нормали к плоскости – это коэффициенты перед переменными в ее уравнении. .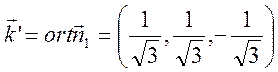

Вектор, сонаправленный прямой , можно найти как векторное произведение векторов нормалей к плоскостям  и :

.

, 

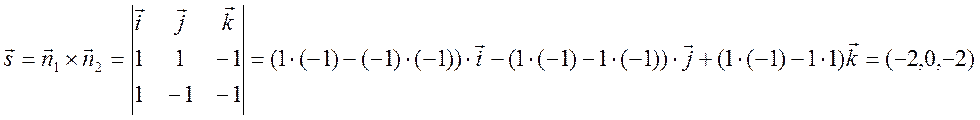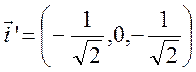
Вектор, сонаправленный  найдем, вычислив векторное произведение  и . Напомним, что тройка (- левая. (см. стр. ).

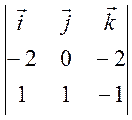=)= (2,-4,-2)=-2(1,-2,-1),   .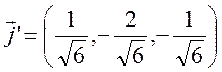

Итак, матрица  перехода от базиса  к базису имеет вид:

== -

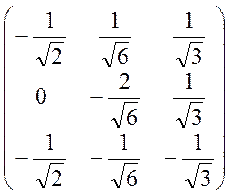
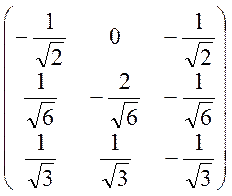
(Вычисление элементов матрицы  выполните самостоятельно).

3. Умножим нормальные векторы плоскостей  и  на матрицу :

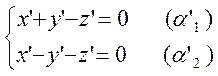
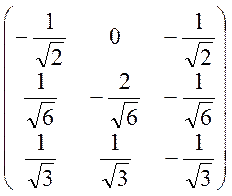
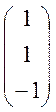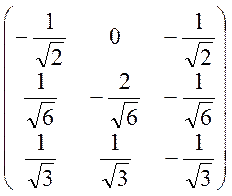
= - =(0,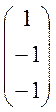0,-),

= - =(0,-,-).

Уравнения плоскостей ,  и общее уравнение прямой  в репере  имеет вид:

 .

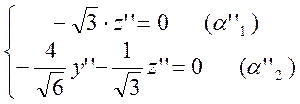
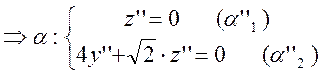Обратим внимание на следующий факт: , то есть, чтобы найти матрицу, обратную матрице перехода от одного ортонормированного базиса к другому, достаточно ее транспонировать.