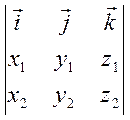Уравнения плоскости и прямой, страница 2

==

 перпендикулярно обоим векторам, а следовательно, перпендикулярно и плоскости . Если выбрать  вектором нормали к плоскости: =, то имеем случай, когда плоскость задана способом 1.  Дальнейшие рассуждения аналогичны приведенным выше. После соответствующих выкладок, получаем:

Раенство (6. 6) называют детерминантным уравнением плоскости. Легко видеть, что введя соответствующие обозначения и выполнив несложные преобразования, мы вновь получаем общее уравнение плоскости.

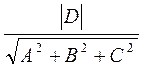Таким образом, как бы ни была задана плоскость, в выбранном репере она имеет уравнение , где -переменные, координаты произвольной точки плоскости, - координаты вектора, перпендикулярного плоскости,  - расстояние от начала координат до плоскости.

Если плоскость параллельна одной из осей координат, то вектор нормали перпендикулярен этой оси, и соответствующая его координата равна 0:

 Если плоскость перпендикулярна одной из осей координат, то вектор нормали параллелен  этой оси, и две его координаты становятся равными 0:

Проанализируем общее уравнение плоскости с алгебраической точки зрения. Рассмотрим случай, когда , ,. Уравнение  является линейным уравнением с тремя переменными (). Две любые переменные могут принимать произвольные значения, то есть являются свободными переменными, а третья выражается через них, то есть является базисной. Пусть свободные переменные – это   и , а - базисная переменная. Разделим уравнение на :  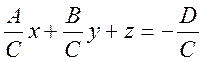или , где 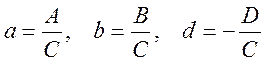. Положим: , . Множество решений уравнения имеет вид:

Перепишем последнее равенство в виде системы:

Система (6.8) представляет собой параметрическое уравнение плоскости. Ее можно рассматривать как систему трех уравнений с двумя свободными переменными ,  и тремя базисными . Свободные переменные  и  называют параметрами.

Все виды уравнений плоскости могут быть приведены к уравнению: . Справедлива теорема.

Теорема об общем уравнении плоскости. В любом репере произвольная плоскость может быть задана общим уравнением . Геометрическим образом этого уравнения в любом репере является плоскость.

В заключение приведем векторное уравнение плоскости:

где =- радиус-вектор произвольной точки плоскости, - радиус-вектор известной, фиксированной точки плоскости,  - вектор нормали к плоскости.

6.3. Уравнения прямой на плоскости

Пусть на плоскости задан ортонормированный репер  (или декартова прямоугольная система координат) и указаны координаты двух точек  и . Проведем через эти точки прямую. Возьмем на ней произвольную точку , не совпадающую с или . Рассмотрим векторы =  и =. Эти векторы коллинеарны: ‌ ‌ , а следовательно их координаты пропорциональны:

Координаты любой точки, лежащей на прямой, удовлетворяют данному равенству. Если же точка не лежит на прямой, то ее координаты данному равенству не удовлетворяют. Равенство (6.10) называют уравнением прямой, проходящей через две заданные точки.

Уравнение (6.10) содержит две переменные  и четыре числа: . Выполнив операции над числами и несложные преобразования с равенством (6.10), получаем уравнение:

где , , .

Обратим внимание на то, что уравнение (6.11) совпадает с уравнением плоскости перпендикулярной . Такое совпадение не случайно: прямую лежащую в плоскости можно рассматривать как линию пересечения двух плоскостей:  и , а уравнение (6.11) - как решение системы:

Пусть теперь прямая задана вторым способом (см. стр.  ), то есть задана точка , через которую она проходит, и вектор , которому прямая параллельна. Заданный вектор  называют направляющим вектором прямой. Воспользовавшись теми же рассуждениями, что и при выводе уравнения прямой, проходящей через две заданны точки, получим уравнение:

Уравнение (6.13) называют каноническим уравнение прямой. Выполнив преобразования равенства (6.13), вновь приходим к уравнению (6.11), либо к системе (6.12), где , , . Рассмотрим векторы , и . Скалярное произведение , следовательно , следовательно вектор  есть вектор перпендикулярный прямой, то есть вектор нормали к прямой. Это приводит к выводу, который часто используется при решении задач: числа   в уравнении прямой на плоскости есть координаты вектора нормали к прямой.

Из уравнения (6. ), приравняв дроби к параметру , получим параметрическое уравнение прямой:

Если из канонического уравнения прямой выразить и ввести соответствующие

Пусть - какая либо прямая на плоскости. Все уравнения прямой на плоскости с заданной системой координат можно привести к виду: . Для более компактной записи это уравнение принято записывать так:

что, естественно, не меняет геометрический смысл чисел  и : - вектор нормали к прямой. Легко показать, что 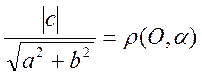есть расстояние от начала координат до прямой . Уравнение (6.16) называют общим уравнением прямой на плоскости.

Справедлива теорема:

Теорема об общем уравнении прямой на плоскости.  Всякую прямую на плоскости в любом репере можно задать уравнением . Геометрическим образом такого уравнения в любом репере является прямая.

6.4. Уравнения прямой в трехмерном пространстве