Теория цепей и электрических сигналов. Сигналы в электротехнике и теории цепей

Теория цепей  и электрических сигналов

                           НАУКА   изучает    НАУЧНЫЕ    свойства  НАУЧНЫХ    примитивов, функциональные  при   научных   преобразованиях.

Примитивы  электротехники (радиотехники):

·  Активное сопротивление   

·  Емкостное сопротивление     

·  Индуктивное сопротивление                                                                           

В электротехнике  и теории цепей и сигналов   используются:

1.  Законы Кирхгофа  (для трех цепей);

2.  Эквивалентные преобразования  электрических элементов:

·  Последовательное  включение элементов (при этом складываются сопротивления)

·  Параллельное включение элементов (при этом складываются величины- обратные сопротивлению – т.н.  «проводимость».

·  Преобразования соединения элементов «звездой»  в соединение «треугольник».

3.  Полная  принципиальная схема  обычно содержит более чем три электрические цепи, а уравнений Кирхгофа можно составить только три для суммы токов выходящих из узла трех цепей и суммы токов входящих в узел трех цепей. Таким образом – с помощью эквивалентных преобразований полная принципиальная схема преобразуется до вида, когда в схеме не более трех цепей, с помощью уравнений Кирхгофа определяются токи в цепях, а затем с помощью обратных эквивалентных  преобразований восстанавливают полную принципиальную схему и определяют токи и напряжения на каждом конкретном элементе.

                            При  рассмотрении  взаимодействия  различных  электрических  сигналов с элементами электрической цепи различают:

1.  Виды сигналов:  по форме, периодичности, детерминированности (случайные или функциональные).

2.  Математические модели сигналов -  S (t)  или U (t)

Математические  модели задаются в виде  аналитических выражений, графиков, таблиц значений, чаще всего – комбинацией заданных элементарных функций.

3.  Преобразование, которое схема осуществляет над сигналом:

       - токовое (изменение тока);

       - напряжения (изменение напряжения);

      - частотное (изменение частоты сигнала);

Чаще всего схема осуществляет над сигналом  комплексное преобразование .

4.  Преобразования чаще всего описываются как некоторые математические действия (операторы) над величинами, описывающими сигнал (ток, напряжение, частота, форма сигнала и т.д.). В качестве операторов используются различные математические модели: функции и их производные, дифференциальные уравнения, системы уравнений, матрицы и матричные операторы и т.д.

ТИПЫ    ШКАЛ

1.  Индексная   шкала- на которой отображаются  цифры  (знаки, индексы )

                            Никаких арифметических (математических действия на этой шкале

производить НЕЛЬЗЯ !!!

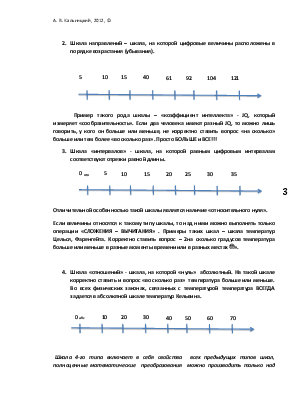
2.  Шкала направлений – шкала, на которой цифровые величины расположены в порядке возрастания (убывания).

                 Пример такого рода шкалы – «коэффициент интеллекта» - JQ, который измеряет «сообразительность». Если два человека имеют разный JQ, то можно лишь говорить, у кого он больше или меньше, не корректно ставить вопрос «на сколько» больше или тем более «во сколько раз». Просто БОЛЬШЕ и ВСЕ!!!                                              

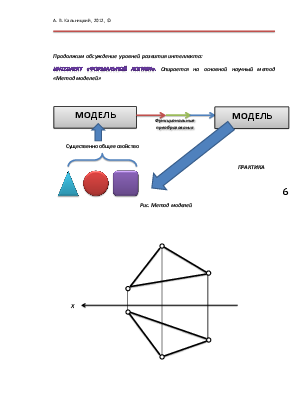
3.  Шкала «интервалов» - шкала, на которой равным цифровым интервалам соответствуют отрезки равной длины.

Отличительной особенностью такой шкалы является наличие «относительного нуля».

Если величины относятся к такому типу шкалы, то над ними можно выполнять только операции «СЛОЖЕНИЯ – ВЫЧИТАНИЯ» . Примеры таких шкал – шкала температур Целься, Фаренгейта. Корректно ставить вопрос – 2на сколько градусов температура больше или меньше в разные моменты времени или в разных местах J».

4.  Шкала «отношений» - шкала, на которой «нуль»  абсолютный. На такой шкале корректно ставить и вопрос «во сколько раз»  температура больше или меньше. Во всех физических законах, связанных с температурой температура ВСЕГДА  задается в абсолютной шкале температур Кельвина.

 Шкала 4-го типа включает в себя свойства  всех предыдущих типов шкал, полноценные математические  преобразования  можно производить только над величинами, принадлежащими шкале «отношений». В радиотехнике очень часть используют т.н. «нормирование», которое  в  качестве  метрики  использует

«разность сигналов», «разность потенциалов», а это значит, что  величины, отображаемые в таком нормированном пространстве, принадлежат к типу шкал –

ИНТЕРВАЛОВ !!!

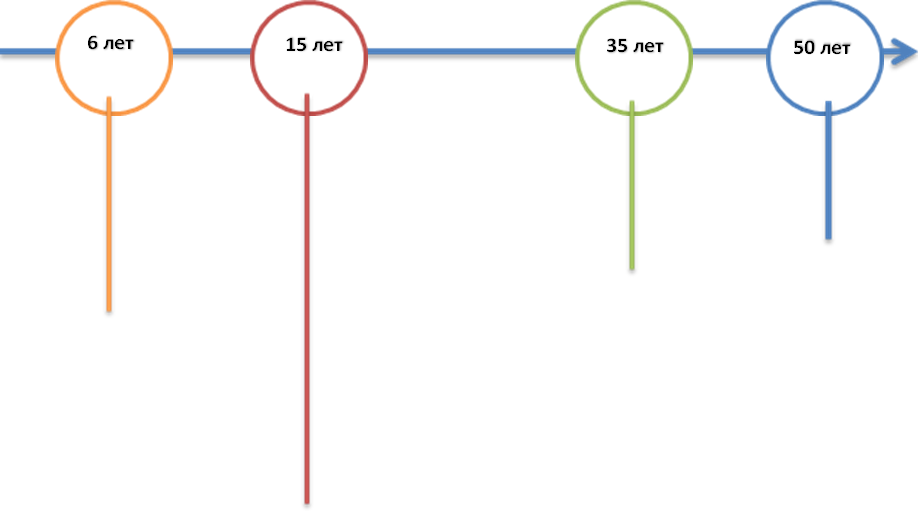
уровни развития интеллекта человека

формальной   теоретический

логики интеллект

Дооперационный

          интеллект

Конкретных

                               операций

На уровне  6 лет  ребенок  не умеет совершать интеллектуальных операций, поэтому этот уровень интеллекта и называется  ДООПЕРАЦИОННЫМ. Ребенок судит о происходящем  по тому что ВИДИТ, ощущает. Его реакция на  чисто математические задачки часто ПАРАДОКСАЛЬНА. Скажем, Вы спрашиваете 6 летнего ребенка : «У тебя яблочко и у меня. Сколько у меня будет яблок, если ТЫ МНЕ ОТДАШЬ СВОЕ ?»

Это неправильная постановка  задачи – ребёнку не до математики, он просто не ХОЧЕТ  ОТДАВАТЬ ВАМ СВОЕ ЯБЛОЧКО! Спросите у него «правильно» - «Сколько яблок будет у тебя, если Я ТЕБЕ ОТДАМ СВОЕ ЯБЛОКО?»  и вы услишите правильный ответ – два! J

На интервале от 6 до 15 лет  ребенок проходит следующие стадии – он начинает совершать интеллектуальные операции начиная манипулировать последовательно следующими  примитивами (простейшими объектами):

ПРИМИТИВ  - РИСУНОК (ФОТО) ПРИМИТИВА - ЧЕРТЕЖ ПРИМИТИВА – СХЕМА

ПРИМИТИВА – СЛОВЕСНОЕ ОПИСАНИЕ ПРИМИТИВА