К 15 ГОДАМ ШКОЛЬНИК ДОЛЖЕН УМЕТЬ СОВЕРШАТЬ ИНТЕЛЛЕКТУАЛЬНЫЕ ОПЕРАЦИИ ПРИ СЛОВЕСНОМ ОПИСАНИИ ЗАДАЧИ!
- Представьте себе СФЕРУ, описанную вокруг куба. Объем какого тела больше? (операция сравнения). А площадь поверхности?
Правильными ответами является – шара( как тела, ограниченного поверхностью – сферой), так как сфера описана вокруг куба, но совершенно очевидным становится ответ при использовании чертежа (рисунка)
 |
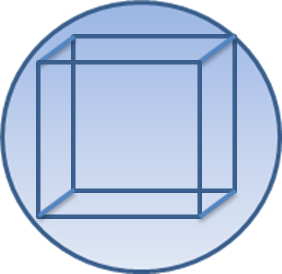Рис. Сфера, описанная вокруг куба
Принципиальным препятствием для студентов ВУЗов является то обстоятельство, что ДЛЯ УСПЕШНОЙ УЧЕБЫ ОНИ УЖЕ ДОЛЖНЫ ОБЛАДАТЬ УРОВНЕМ ИНТЕЛЛЕКТА либо 35-летнего кандидата наук, либо 50-летнего доктора наук J.
Продолжим обсуждение уровней развития интеллекта:
Интеллект «Формальной логики». Опирается на основной научный метод «Метод моделей»
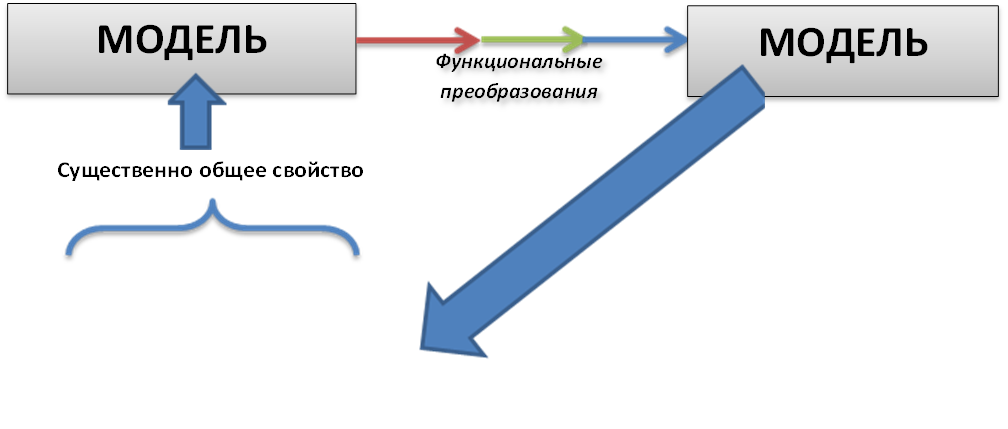
ПРАКТИКА
Рис. Метод моделей
 |
|||
 |
|||
Пример: Чертеж плоской фигуры
Это модель (графическая) в первоначальном виде, как она нам дана. Ни одна из проекций треугольника не является натуральной величиной и поэтому в этом треугольнике я ничего пока что не могу измерять. Сначала необходимо найти натуральную величину треугольника, каким либо способом. Инженерная графика уже сдана и я полагаю, что Максим легко справится с такой задачей.
Общее определение науки.
______________________________ ИЗУЧАЕТ _______________________ СВОЙСТВА
______________________________ ПРИМИТИВОВ, ФУНКЦИОНАЛЬНЫЕ (ИНВАРИАНТНЫЕ) ПРИ _________________________ ПРЕОБРАЗОВАНИЯХ.
( А. В. Кальницкий)
ГЕОМЕТРИЯ изучает ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ГЕОМЕТРИЧЕСКИХ ПРИМИТИВОВ ФУНКЦИОНАЛЬНЫЕ при ГЕОМЕТРИЧЕСКИХ преобразованиях
химия изучает химические свойства химических примитивов функциональные при химических преобразованиях
физика изучает физические свойcтва физических примитивов функциональные при физических преобразованиях
математика изучает математические свойства математических примитивов функциональные при математических преобразованиях
Основным математическим примитивом является РАВЕНСТВО
А + В = С + D
Математические преобразования, применяемые в равенству:
1. Умножение каждой части равенства на одно и то же число (не равное нулю);
2. Деление обеих частей равенства на число не равное нулю;
3. Добавление к частям равенства одного и того же числа, а равно и вычитание его;
4. Логарифмирование частей равенства и обратное действие – потенциирование;
5. Дифференцирование и интегрирование частей равенства;
6. Извлечение корня;
7. Возведение в степень (необходимо не забывать, что в этом случае возможно появление побочного корня);
и др. преобразования
Я уже говорил, что уровень интеллекта «формальной логики» соответствует ученой степени «кандидат наук». Чем же этот уровень отличается от уровня интеллекта «Теоретический» ? Если кандидат наук изучает относительно узкую тему, скажем «Колебания крыла самолете в сверхзвуковом полете», а второй – «Колебания индекса Доу-Джонса на бирже Нью-Йорка», а третий «Колебания уровня воды в створе ГЭС», то их руководитель (как правило доктор наук)- просто обязан быть специалистом в вопросе «КОЛЕБАНИЕ И ВОЛНЫ». Его теоретическая модель должна основываться на общих существенных свойствах и колебаний крыла, и индекса Доу-Джонса, и воды…
Если кандидат наук решает научным методом (метод моделей)
одну научную задачу, то доктор наук – решает КЛАСС ЗАДАЧ, куда составляющие
класс задач задачи входят как частные случаи.
REM для родителей
Вот мне и придется
основное время потратить на вывод Вашего сына сначала на уровень «формальной
логики», а потом уже и на уровень «теоретический», хотя этот процесс и можно
ускорить, но перепрыгнуть через стадию «формальной логики» все же НЕЛЬЗЯ.
Приведу пример решения одной и той же задачи на трех уровнях интеллекта – 2,3 и 4-м.
ЗАДАЧА: найти сумму ряда
S= 1+2+3+…….+100
На уровне «конкретных операций» мы просто складываем последовательно числа от 1 до 100 и примерно через 20 минут получим результат – 5050.
На уровне «формальной логики» нужно сначала найти какое-то существенное свойство в этой задаче -
Сложим сначала сумму первого десятка 1+2+3+4+5+6+7+8+9+10 = 55
Второй десяток даст 11+12+13+14+15+16+17+18+19+20 = 155
Сумма каждого последующего десятка на 100 больше !!! Действительно, ведь 11= 1+10, а 12= 2+ 10… и т.д., поэтому второй десяток мы можем представить как сумму от 1 до 10 и 10 раз по 10 – итого 55+ 100 = 155. Следовательно, последний -9-й десяток даст в сумме 955, значит сумму от 1 до 100 мы можем представить так:
10 раз по 55 = 550
45 х 100 (сумма сотен) = 4500
В сумме 4500 + 550 = 5050, этот результат мы получили значительно быстрее, примерно за 5 минут.
Решение задачи суммы ряда в общем виде – на теоретическом уровне интеллекта:
Запишем наш ряд в общем виде:
S = 1+2+3+………………………………………..( n-2) + (n-1) + n
Теперь под первым рядом запишем точно такой же второй, только переписанный «задом-на-перед»
S = 1 + 2 + 3 +………………………………………..(
n-2) + (n-1) + n
S = n + (n-1) + (n-2) +…………………………………………+ 3 + 2 + 1
Теперь сложим оба ряда и результат поделим на 2 (так как мы складываем два ОДИНАКОВЫХ ряда )
S = (n+1)n | 2 - эту формулу суммы натурального ряда Гаусс
вывел в 10 лет (!), значит можно и в 10, а не в 50 лет обладать «теоретическим
уровнем интеллекта» J.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.