Схема замещения однородной двухпроводной линии, телеграфные уравнения

l720

Схема замещения однородной двухпроводной линии, телеграфные уравнения.

На рис. 1 изображена схема двухпроводной линии, где:

x − расстояние от начала линии до рассматриваемого элементарного участка dx.

l − длина линии;

u(t,x) и i(t,x) − текущее значение напряжения и тока в  линии;

u₁(t,x=0) и i₁(t,x=0) − напряжение и ток в начале линии;

u₂(t,x=l) и i₂(t,x=l) − напряжение и ток в конце линии.

Верхний провод двухпроводной линии называют прямым проводом, а нижний обратным проводом. Зададим положительные направления напряжения и тока u(t,x) и i(t,x), (рис. 1).

 

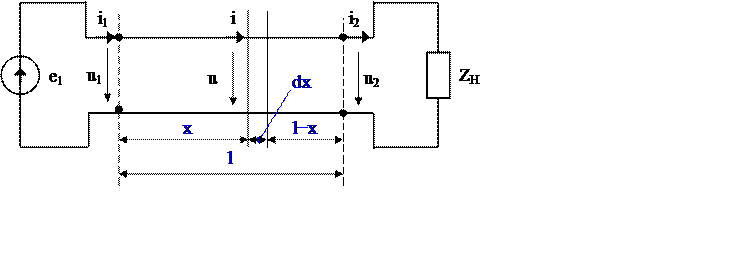Рис. 1

Рассмотрим первичные  погонные параметры схемы замещения элементарного участка «dx» двухпроводной длинной линии (рис. 2), приходящимся на единицу длины, и основные физические процессы, которые они  учитывают:

●  R₀ − активное сопротивлением проводов, размерность Ом/км, учитывает тепловые потери электрической энергии при протекании тока в проводе;

●  L₀ − индуктивность участка линии, размерность Гн/км, учитывает явление самоиндукции от магнитного поля возникающего вокруг проводов и вызванного протеканием по проводнику переменного тока i(t,x);

●  C₀ − ёмкость участка линии, размерность Ф/км; учитывает токи смещения между проводами линии обусловленные электрическим полем создаваемым переменным напряжением u(t,x) между проводами линии;

●  G₀ − проводимость участка линии, размерность См/км, учитывает ток проводимости между проводами линии, обусловленный электрическим полем, создаваемым переменным напряжением u(t,x) между проводами линии и не идеальный диэлектриком, в котором расположены провода;

Для однородной линии первичные параметры распределены равномерно.

Пусть известны первичные параметры линии. Длинную линию представим в виде множества соединенных в цепочку бесконечно малых элементов длиной «dx», каждый из которых имеет схему замещения (рис. 2) с последовательным соединением сопротивления − R₀dx и индуктивности − L₀dx, а также параллельным соединением проводимости − G₀ dx и емкости − C₀ dx.

Так как u(t,x) и i(t,x) являются функцией двух переменных - x и t , то необходимо рассматривать частные производные от этих функций.

Составим дифференциальные уравнения, которым удовлетворяют напряжения и токи в любом сечении двухпроводной линии.

 

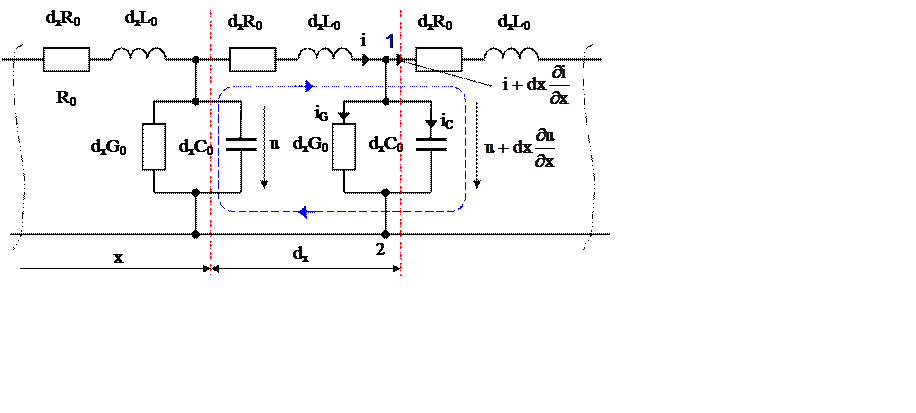Рис. 2

По первому закону Кирхгофа для узла 1:

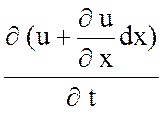i − (i − dx) − g₀ dx (u + dx) − C₀ dx =0.

Пренебрегая величинами второго порядка малости, получим:

− = u g₀ + C₀ .                                                                                                      (1)

По второму закону Кирхгофа для заданного контура:

u = iR₀ dx + L₀ dx + u + dx     или

− = i R₀ + L₀ .                                                                                                      (2)

Система уравнений (1) и (2) пользуются для расчета любых режимов работы однородной двухпроводной линии.