L. 450. «Электротехника» Аксютин В.А.
Расчет линейной цепи
с несинусоидальными периодическими источниками.
Традиционная постановка задачи расчёта цепей несинусоидального тока: по заданным несинусоидальным ЭДС и параметрам R – L – C элементов необходимо рассчитать мгновенные i(t) и действующие I значения токов, определить P, Q, S цепи.
Расчёт выполняется в три этапа:
1. Представление заданного несинусоидального напряжения в виде набора гармоник рядом Фурье. Разложение в ряд Фурье проводится: аналитически по интегральным соотношениям; численными или экспериментальными методами.
2. Расчёт цепи проводится методом наложения отдельно для каждой из гармоник.
·
Расчёт для нулевой гармоники выполняется
также как для цепей постоянного тока. Для нулевой гармоники k = 0 X![]() = 0 wL = 0, X
= 0 wL = 0, X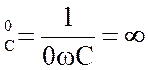 .
.
· Расчёт цепи для основной и высших гармоник проводится, как для линейной цепи синусоидального тока символическим методом. Особенностью расчётов является то, что реактивные сопротивления XL и XC для разных гармоник будут различны:
X![]() = kwL = k x
= kwL = k x![]() ,
X
,
X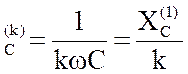 (1)
(1)
3. Запись результирующих мгновенных значений i(t), u(t) и построение графиков. Определение постоянных составляющих, действующих значений, показания приборов, а также коэффициентов, характеризующих несинусоидальные функции: КА, КФ, КИ и КГ.
Пример 1.
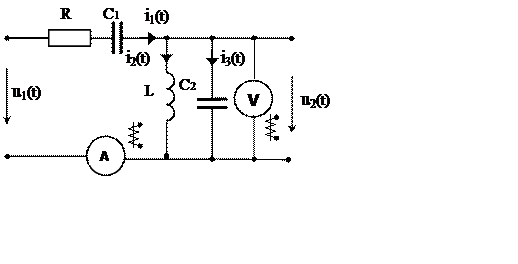 |
|||
 |
|||
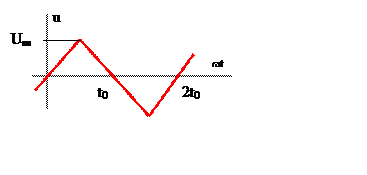
а б
Рис. 1
На вход схемы рис. 1а подключён источник пилообразного напряжения u1(t) (рис. 1б): Um =10 В. T = 2t0 = 10–3с.
R=100 Ом, L=0.005 Гн, C1=0.5 мкФ, C2=1.0 мкФ.
1. Определить мгновенные значения входного тока i1(t) и выходного напряжения u2(t); построить графики u1(t), u2(t) и i1(t) по 1, 3 и 5 гармоникам.
2. Определить показания вольтметра и амперметра электромагнитной системы. Для входного и выходного напряжения определить коэффициенты КА, КФ, КИ и КГ.
Решение
1. Представим заданное несинусоидальное напряжения u(t) рис. 1б в виде набора гармоник ряда Фурье. (раздел l 410, табл. 1). Ограничимся 1, 3 и 5 гармониками.
u1(t) = 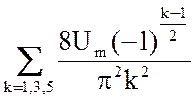 sin(k ω t) (2)
sin(k ω t) (2)
Подставив исходные данные в (2) получим гармонический ряд
u1(t) = 8.11 sin(ωt) – 0.901 sin(3ωt) + 0.324 sin(5ωt). (В).
Графики составляющих ряда и результирующая кривая показана на рис.2:
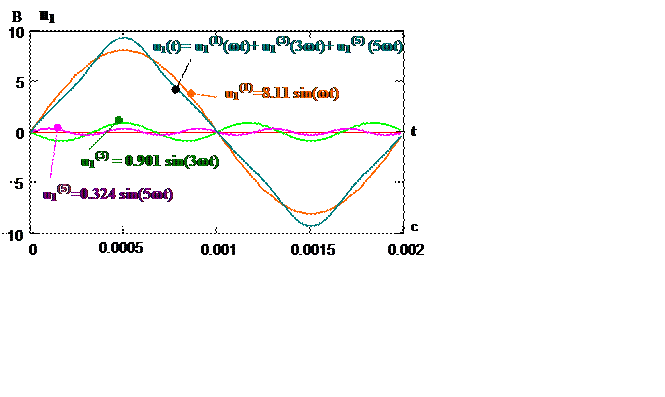 |
Рис. 2
2. Расчёт цепи символическим методом по 1, 3 и 5 гармоникам.
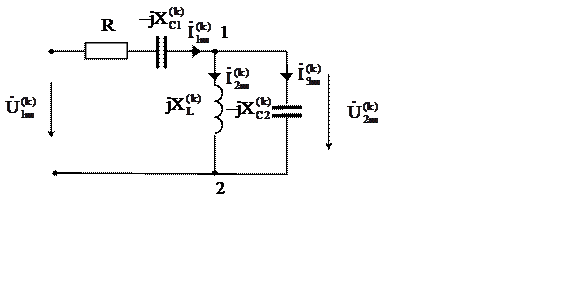 |
Рис. 3
Составим схему замещения цепи в комплексном виде для расчёта действующих значений токов и напряжений k – й гармоники (рис. 3).
Угловая частота - w = 2π ∕ T =2π ∕ 10–3 = 6.28 10+3 =6280 рад/с.
Реактивные сопротивления для k – й гармоники (1):
X![]() = kwL = k X
= kwL = k X![]() ,
X
,
X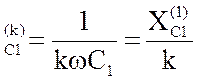 = X
= X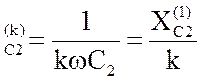
Формулы для расчётов комплексных амплитуд токов и напряжений для k – й гармоники:
Z![]() =
= 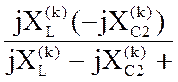 ;
; ![]() =
= 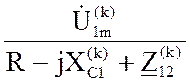 ;
;
![]() = Z
= Z![]()
![]() ;
; ![]() =
= 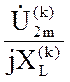 ;
; ![]() =
= 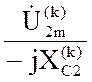 .
.
2.1. Первая гармоника k=1.
Реактивные сопротивления
x![]() = wL = 31.4 Ом, x
= wL = 31.4 Ом, x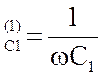 = 318
Ом, x
= 318
Ом, x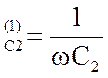 = 159 Ом,
= 159 Ом,
Z![]() = j 39.1
Ом;
= j 39.1
Ом;
![]() = 0.00921 + j 0.026 = 0.027Ð70.3º A.
= 0.00921 + j 0.026 = 0.027Ð70.3º A.
![]() = − 1.007 + j 0.361 = 1.07Ð160.3º В.
= − 1.007 + j 0.361 = 1.07Ð160.3º В.
![]() = 0.011 + j 0.032 = 0.034Ð70.3º A.
= 0.011 + j 0.032 = 0.034Ð70.3º A.
![]() = − 0.00227 − j 0.00633 = 0.00672Ð−109.7º A.
= − 0.00227 − j 0.00633 = 0.00672Ð−109.7º A.
2.2. Третья гармоника k=3.
X![]() = 3wL = 3 x
= 3wL = 3 x![]() =94.2 Ом; X
=94.2 Ом; X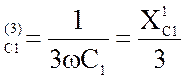 =106
Ом;
=106
Ом;
X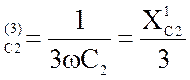 =53 Ом;
=53 Ом;
Z![]() = −j 121 Ом;
= −j 121 Ом;
![]() = 0.00146 + j 0.00332 = 0.00383Ð66.3º A.
= 0.00146 + j 0.00332 = 0.00383Ð66.3º A.
![]() = +0.403 − j 0.177 = 0.44Ð−23.7º В.
= +0.403 − j 0.177 = 0.44Ð−23.7º В.
![]() = −0.00188 − j 0.00427 = 0.00457Ð−114º A.
= −0.00188 − j 0.00427 = 0.00457Ð−114º A.
![]() = 0.00334 + j 0.00759 = 0.00829Ð+66.3º A.
= 0.00334 + j 0.00759 = 0.00829Ð+66.3º A.
2.2. Пятая гармоника k=5.
x![]() = 5wL = 5 x
= 5wL = 5 x![]() = 157 Ом; X
= 157 Ом; X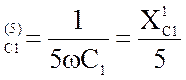 =63.6 Ом;
=63.6 Ом;
X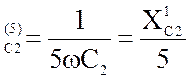 = 31.8 Ом;
= 31.8 Ом;
Z![]() = −j 39.9 Ом;
= −j 39.9 Ом;
![]() = 0.00156 − j 0.00162 = 0.00225Ð46º A.
= 0.00156 − j 0.00162 = 0.00225Ð46º A.
![]() = 0.065 + j 0.062 = 0.09Ð−44º В.
= 0.065 + j 0.062 = 0.09Ð−44º В.
![]() = −0.0004 + j 0.00041 = 0.00057Ð−134º A.
= −0.0004 + j 0.00041 = 0.00057Ð−134º A.
![]() = 0.00196 + j 0.00203 = 0.00282Ð46º A.
= 0.00196 + j 0.00203 = 0.00282Ð46º A.
3. Расчёт итоговых параметров.
3.1. Построение результирующих кривых мгновенных значений:
-входного тока i1(t) (рис. 4):
|
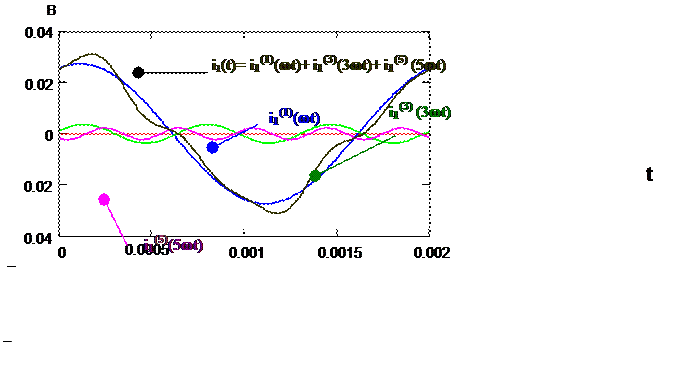 |
Рис. 4
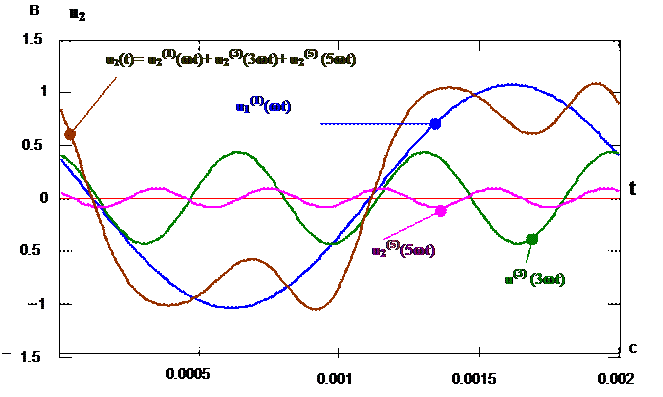
выходного напряжения u2(t) (рис. 4):
u2(t) = 1.07 sin(ωt+160.3º) – 0.44 sin[3(ωt−23.7º)]+ 0.09 sin[5(ωt−44º)]. (В).
|
|||
 |
|||
Рис. 5
3.2. Определение действующих значений и показание вольтметра и амперметра электромагнитной системы.
I![]() = I
= I![]() /√2 = 0.027/√2 = 0.0191 A;
/√2 = 0.027/√2 = 0.0191 A;
I![]() = I
= I![]() /√2 = 0.00383 /√2 =0.00271 A;
/√2 = 0.00383 /√2 =0.00271 A;
I![]() = I
= I![]() /√2 = 0.00225 /√2
= 0.00159 A;
/√2 = 0.00225 /√2
= 0.00159 A;
I1 = ![]() =
0.02 A.
=
0.02 A.
U![]() = U
= U![]() /√2 = 1.07/√2 = 0.757 B;
/√2 = 1.07/√2 = 0.757 B;
U![]() = U
= U![]() /√2 = 0.44 /√2 = 0.311 B;
/√2 = 0.44 /√2 = 0.311 B;
U![]() = U
= U![]() /√2 = 0.09 /√2 = 0.0636 B;
/√2 = 0.09 /√2 = 0.0636 B;
U2 = ![]() = 0.82 B
= 0.82 B
3.3. Определение коэффициенты КА, КФ, КИ и КГ для выходного напряжения.
U2 ср по mod = (U![]() + U
+ U![]() + U
+ U![]() )/1.11=1.02 В
)/1.11=1.02 В
![]() формы KФ =
формы KФ = 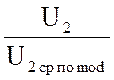 =
= 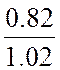 = 0.804;
= 0.804;
![]() амплитуды KA =
амплитуды KA = 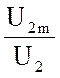 =
= 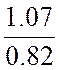 = 1.3;
= 1.3;
![]() искажения KИ =
искажения KИ = 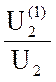 =
= 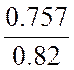 = 0.923;
= 0.923;
![]() гармоник KГ =
гармоник KГ = 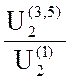 =
= 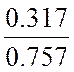 =
0.419.
=
0.419.
Пример 2.
 |
|||
 |
|||
а б
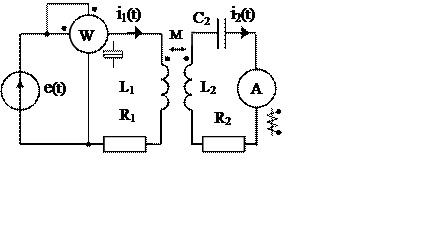
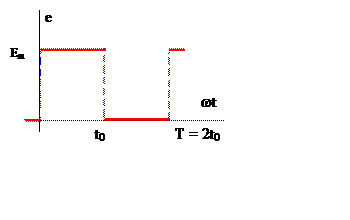
Рис. 6
На вход схемы рис. 6,а подключён источник импульсной ЭДС
e(t) (рис. 6б): Em =100 В. T = 2t0 = 10–2с.
R1 = 50 Ом, R2 = 20 Ом, L1 = 0.2 Гн, L2 = 0.1 Гн, M = 0.1Гн,
C2 = 50 мкФ.
Определить показания ваттметра электродинамической системы и амперметра электромагнитной системы.
Решение
1. Представим заданное несинусоидальное напряжения u(t) рис. 6б в виде набора гармоник ряда Фурье (раздел l 410, табл. 1). Ограничимся 0, 1, 3 и 5 гармониками.
e(t) =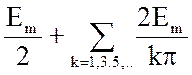 sin(kwt)= 50+
sin(kwt)= 50+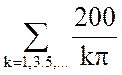 sin(kwt) (10)
sin(kwt) (10)
e(t) = 50 + 63.7 sin(wt) +21.2 sin(3wt)+ 12.7 sin(5wt)
E0 = 50 B – постоянная составляющая;
E(k) = 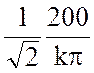 =
= ![]() –
действующее значение ЭДС k – й
гармоники.
–
действующее значение ЭДС k – й
гармоники.
w = 2π ∕ T =2π ∕ 10–3 = 628 рад/с. – угловая частота основной гармоники.
2. Расчёт цепи символическим методом по 0, 1, 3 и 5 гармоникам.
 |
|||||
|
|||||
 |
|||||
а б
Рис. 7
2.1.Нулевая гармоника k=0.
Составим схему замещения цепи для расчёта токов по нулевой гармонике (рис. 7,а). Определим ток и мощность по первой гармонике:
![]() =
=![]() =
=
![]() = 1 A
= 1 A
![]() =
=![]() = E0
= E0![]() = 50 1 =50 Вт
= 50 1 =50 Вт
2.2. Гармоники k=1, 3, 5.
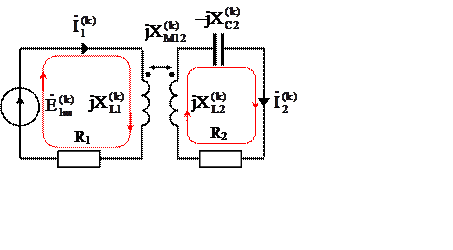
2.2.1.- Составим схему замещения цепи в комплексном виде для расчёта действующих значений токов и мощностей гармоник (рис. 7,б).
2.2.2.- Определим параметры схемы:
Комплекс действующего значения ЭДС k – й гармоники:
![]() =
= ![]() Ð0º B
Ð0º B
Реактивные сопротивления
─ для первой гармоники (1):
X![]() = w L1 =314 *
0.2 = 62.8 Ом.
= w L1 =314 *
0.2 = 62.8 Ом.
X![]() , = w L2 =314 * 0.1 = 31.4 Ом.
, = w L2 =314 * 0.1 = 31.4 Ом.
X![]() = w M =314 * 0.1 = 31.4 Ом;
= w M =314 * 0.1 = 31.4 Ом;
X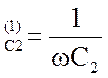 = 1/(314
* 50* 10-6 )= 63.7 Ом.
= 1/(314
* 50* 10-6 )= 63.7 Ом.
─ для k – й гармоники:
X![]() = k wL1 = k X
= k wL1 = k X![]() =
k 62.8, X
=
k 62.8, X![]() =
k wL2 = k X
=
k wL2 = k X![]() =
k 31.4,
=
k 31.4,
X![]() = k wМ = k X
= k wМ = k X![]() = k 31.4, X
= k 31.4, X![]() =
= 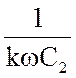 =
=
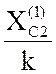 =
= 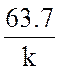 .
.
2.2.3.- Составим формулы для расчётов комплексных токов и мощностей по k – й гармонике:
Расчёт токов по законам Кирхгофа
![]() (R1+ j X
(R1+ j X![]() ) −
) − ![]() j X
j X![]() , =
, = ![]()
−![]() j X
j X![]() +
+ ![]() (R2+j X
(R2+j X![]() − j X
− j X![]() ) = 0
) = 0
Запишем эту систему в матричной форме
|
R1+ j X |
−j X |
´ |
|
= |
|
|
−j X |
R2+j X |
|
0 |
|
50+ j k 62.8 |
−j k 31.4 |
´ |
|
= |
|
|
−j k 31.4 |
20+j k 31.4 − j
|
|
0 |
Δ(k) =
(50+ j k 62.8) (20+j k 31.4 − j 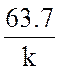 ) – (−j k 31.4 ) (−j k 31.4 ) =
) – (−j k 31.4 ) (−j k 31.4 ) =
= (5000 − 986 k2) + j(2826 k − 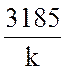 )
)
Δ![]() =
= ![]() (20+j k 31.4 − j
(20+j k 31.4 − j 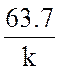 ) =
) = 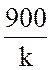 +j (1413 −
+j (1413 − 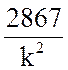 )
)
Δ![]() = −
= − ![]() ( − j k 31.4) = j 1413
( − j k 31.4) = j 1413
2.2.4. Первая гармоника k=1.
![]() =
= 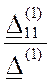 =
= 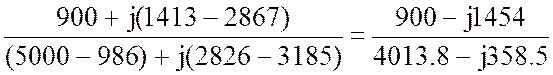 =
=
= 0.254-j 0.34 = 0.423Ð-53° A
![]() =
= 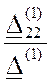 =
= 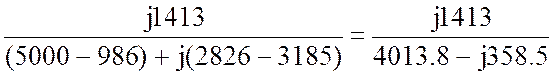 =
=
= -0.031+j0.349= 0.35Ð95.1° A.
2.2.5 Третья гармоника k=3.
![]() =
= 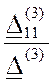 =
= 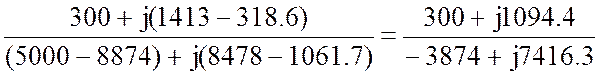 =
=
= 0.0993-j 0.00923 = 0.136Ð-43° A
![]() =
= 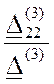 = =
= = 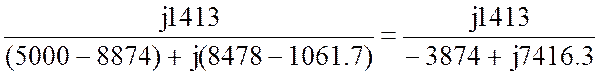 =
=
= 0.15-j0.0782= 0.169Ð-27.5° A.
2.2.6. Пятая гармоника k=5.
![]() =
= 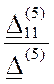 =
= 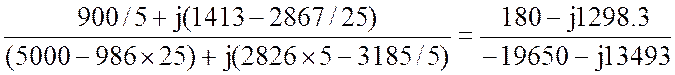 =
=
= 0.0246-j 0.0492 = 0.055Ð-63.4° A
![]() =
= 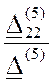 =
= 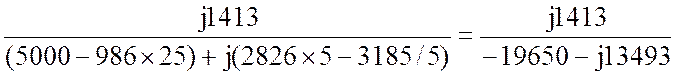 =
=
= 0.0336-j0.0489= 0.0593Ð55.5° A.
3. Mмгновенные значения токов i1(t) и i2(t).
i1(t) = 1 + 0.423√2 sin(wt-53º) + 0.136√2sin[3(wt-43°)]+ 0.055√2sin[5(wt-63°)]A.
i2(t) =0.35√2 sin(wt+95º) + 0.169√2 sin[3(wt-27.5°)]+ 0.0593√2sin[5(wt+55.5°)]A.
4. Показание амперметра A2.
АмперметрA2 показывают действующие значения тока:
I А2 = ![]() =
=
![]() = 0.393 А.
= 0.393 А.
5.. Показание ваттметра.
PW=![]() +
+![]() +
+![]() +
+![]() =
=
= E0![]() +
+ ![]()
![]() cos(0-
cos(0-![]() ) +
) + ![]()
![]() cos(0-
cos(0-![]() )+
)+ ![]()
![]() cos(0-
cos(0-![]() ) =
) =
= 50+ 45´0.423 cos(53) + 15´0.136 cos(43) + 9´0.055 cos(63) =
= 50 + 20.5 + 1.49 + 0.22 = 72.2 Bт
Пример 3.
На
вход схемы рис. рис. 8 подаётся напряжение: ![]() =10+5
sin(1000t)+2 sin(5000t)В.
=10+5
sin(1000t)+2 sin(5000t)В.
Параметры: R=1 кОм, L=0.04 Гн.
Найти значения C1 и C2., которые обеспечивают напряжения на выходе:
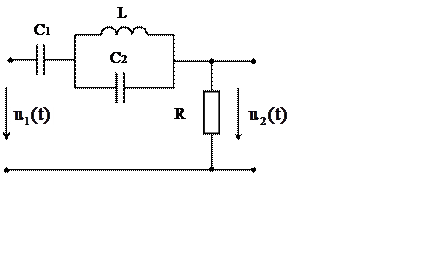
![]() =5sin(1000t) В.
=5sin(1000t) В.
Рис. 8
Решение
Схема рис. 8 представляет частотный фильтр, пропускающий в нагрузку сигнал частоты первой гармоники и задерживающий постоянную составляющую и сигнал пятой гармоники.
1. Постоянная составляющая не поступается в нагрузку конденсатором C1
2. Если настроить параллельный контур L/С2 в резонанс токов на пятой гармонике, то сопротивление контура будет равно бесконечности и в нагрузке напряжение пятой гармоники будет отсутствовать. Из этого условия можно определить величину ёмкости С2
X![]() = w L =1000 * 0.04 = 40 Ом.
= w L =1000 * 0.04 = 40 Ом.
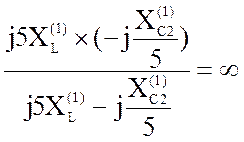 ;
; 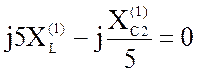 ;
;
![]() Ом
Ом
С2 = 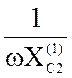 = 10-6Ф = 1 мкФ
= 10-6Ф = 1 мкФ
3. Если настроить фильтр С1, L/С2 в резонанс напряжений на первой гармонике, то сопротивление контура будет равно нулю и в нагрузку напряжение первой гармоники будет передаваться полностью. Из этого условия можно определить величину ёмкости С1:
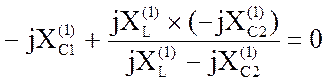
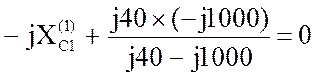
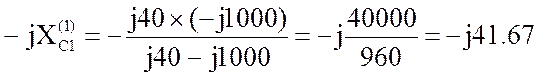 Ом
Ом
С1 = 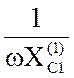 =
= 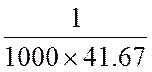 =
24 10-6Ф = 24 мкФ.
=
24 10-6Ф = 24 мкФ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.