L. 625. «Электротехника» Аксютин В.А.
Расчет нелинейной цепи методом последовательных приближений.
1. Линейная аппроксимация нелинейных характеристик
 |
а б
Рис. 1
 |
а б
Рис. 2
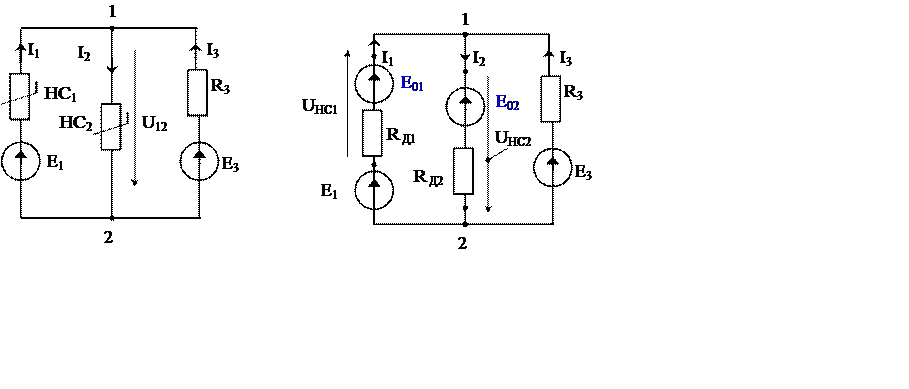
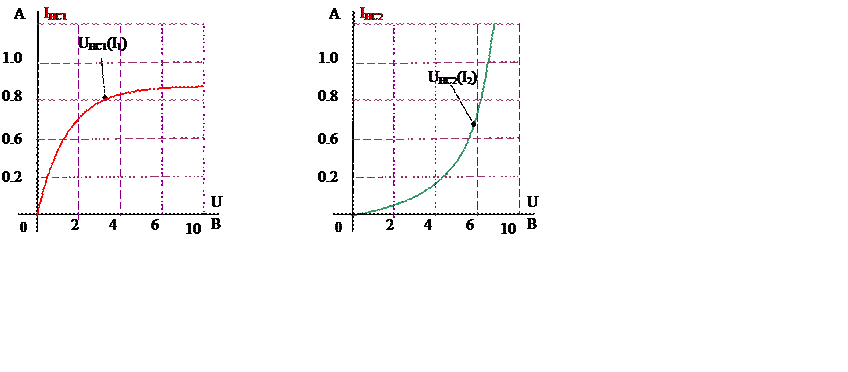
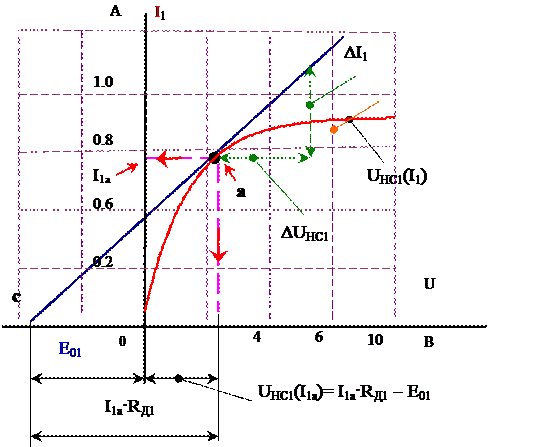
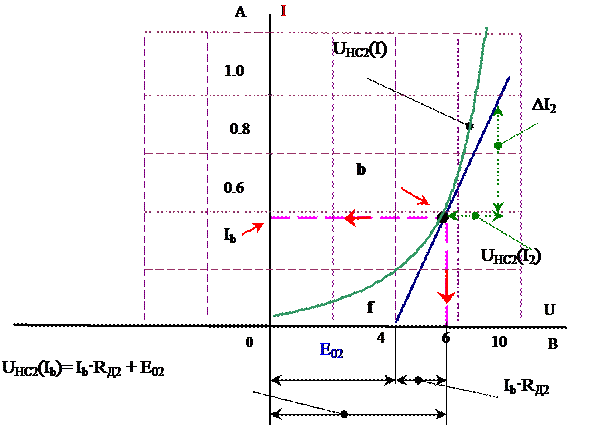
Рассмотрим в качестве примера нелинейную цепь рис. 1а. Пусть известны ВАХ нелинейных элементов (например, HC1 - лампы накаливания, рис. 2а и HC2 – диода, рис. 2б). Пусть также известны режимы работы нелинейных элементов HC1 в точке «а» рис 3а, и HC2 в точке «в» рис 4а, например, значения токов I1a и I2в. Проведём касательные в точках «а» и «b» и продолжим до пересечения с осью абсцисс. В точках пересечения получим значения ЭДС E01 (рис 3а) и E02 (рис 4а).
Определим в точках «а» и «b» дифференциальные сопротивления для первого и второго нелинейных элементов (рис. 3а и 4а):
Rд1 = 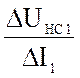 и Rд2 =
и Rд2 = 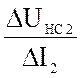 . (1)
. (1)
 |
|||||
 |
|||||
 |
|||||
а б
Рис. 3
 |
|||||
 |
|||||
 |
|||||
а б
Рис. 4
Таким образом, в точках «а» и «в» нелинейные характеристики элементов и HC2, можно представить линейными характеристиками, которые выражается уравнениями:
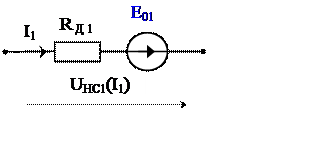
● характеристика HC1 - UHC1(I1)= I1·RД1 - E01 ; (2)
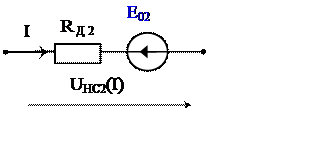
● характеристика HC2 - UHC2(I)= I·RД2 + E02. (3)
Полученные уравнения позволяют получить линейные схемы замещения для соответствующих нелинейных характеристик (рис. 3б и рис. 4б).
После замены нелинейных элементов эквивалентными схемами замещения с линейными элементами нелинейную цепь, например, рис 1а можно представить линейной рис 1б и рассчитывать методами, применяемыми для расчета линейных цепей.
Для примера рис 1б
U12 = 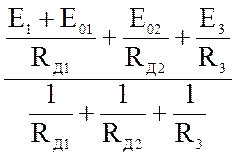 ; (4)
; (4)
I1 = 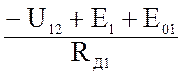 ; I2 =
; I2 = 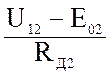 ; I3 =
; I3 = 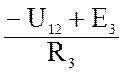 ; (5)
; (5)
Однако, после нахождения токов в цепи нужно убедиться, что нелинейныеt элементы действительно будет работать вблизи рабочих точек «а» и «b» ВАХ элементов.
2. Метод последовательных приближений (итераций)
Метод последовательных приближений основан на линейной аппроксимации нелинейных характеристик. Применяется для расчёта сложных цепей. Суть его заключается в предварительном выборе ожидаемых начальных значений токов или напряжений на нелинейных элементах и затем последовательной их проверки и уточнении.
Порядок расчёта:
1. В исходной цепи предварительно задаются величины токов или
напряжений в нелинейных сопротивлениях. Для примера токи I1 = ![]() и I2 =
и I2 = ![]()
2. По ВАХ сопротивлений в рабочих точках нелинейных сопротивлений определяются параметры линейных зависимостей UHC1(I1)= I1·RД1 - E01 , UHC2(I)= I·RД2 + E02. и схемы замещения нелинейных элементов. Для примера рис. 3 и 4 это RД1, E01, RД2 и E02.
3. Строится линейная схема замещения исходной цепи. Для примера схема приведена на рис. 1а.
4. По линейной схеме замещения любым известным методом
рассчитываются уточнённые значения токов в нелинейных сопротивлениях. Для
примера схема рис. 1а рассчитывается методом двух узлов по соотношениям (4) и
(5) токи I1 = ![]() и I2 =
и I2 = ![]() .
.
5. Задаётся величина погрешности расчёта ε. Проверяется погрешность расчёта. Для примера:
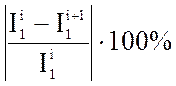 ≤ ε и
≤ ε и 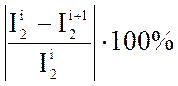 ≤ ε
≤ ε
Если условия выполняется, то процесс расчёта заканчивается
в противном случае в расчёт задаются вновь рассчитанные величины токов, в
примере это I1 = ![]() и I2 =
и I2 = ![]() и
процесс расчёта повторяется.
и
процесс расчёта повторяется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.