L. 532. «Электротехника» Аксютин В.А.
Примеры расчёта переходных процессов с помощью интеграла Дюамеля
Пример 1
На вход цепи, рис. 1а, подаётся напряжение: uВХ (t). Заданы R= 1 кОм, L = 0.05 Гн и график входного напряжения uВХ(t), рис.1б , где U0 = 10 В, t0 = 20 мс,
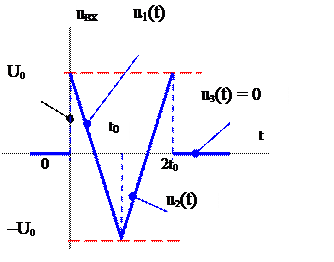 |
|||
 |
|||
а б
Рис. 1
Найти: закон изменения выходного напряжения uВЫХ(t).
Решение
1. Для напряжения uВЫХ(t) классическим или операторным методом рассчитывается переходная функция цепи k(t), как включение цепи на источник постоянной ЭДС 1 В.
|
||||
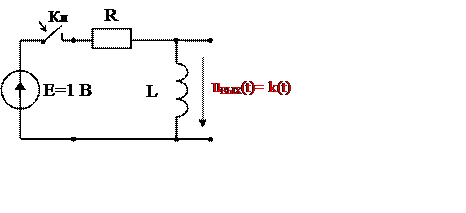 |
||||
Рис. 2
2. Для трёх участков характеристики входного напряжения uВХ(t) источника (рис. 1б), имеющего аналитическое описание и представленного кусочно-гладкой функцией после коммутации, составим интеграл Дюамеля.
![]()
![]()
![]() u1(t) = a1 t + b1, u1(t)
=
u1(t) = a1 t + b1, u1(t)
= 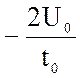 t + U0, u1(t) = –1000 t + 10,
t + U0, u1(t) = –1000 t + 10,
uВХ(t) = u2(t) = a2 t + b2, = u2(t)
= 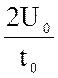 t – 3 U0, = u2(t) = 1000 t – 30,
t – 3 U0, = u2(t) = 1000 t – 30,
u3(t) = 0, u3(t) = 0, u3(t) = 0,
a1 = 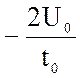 = –1000 В/с. a2
=
= –1000 В/с. a2
= 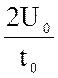 –1000 В/с.
–1000 В/с.
· В промежутке 0<t<t0 можно воспользоваться уже имеющейся формулой (1):
uВЫХ1(t)= u1(0) k(t) + 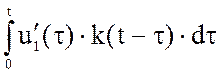 .
.
· В промежутке t0<t<2t0 следует учесть скачок напряжения e2(t1) – e1(t1), а также то, что напряжение изменяется по закону e2(t):
uВЫХ2(t)= u1(0) k(t) + 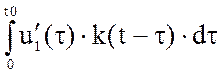 + [u2(t0) – u1(t0)]
k(t–t0) + +
+ [u2(t0) – u1(t0)]
k(t–t0) + +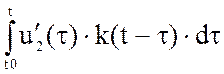 ,
,
где k(t–t1) учитывает запаздывание скачка [u2(t0) – u1(t0)] на время t0 по сравнению с началом отсчёта времени.
·
Для промежутка времени 2t0<t<![]() учитываем скачок - u2(2t0), а
также то, что u2(t)
действует лишь до 2t0:
учитываем скачок - u2(2t0), а
также то, что u2(t)
действует лишь до 2t0:
uВЫХ3(t) = u1(0) k(t) + 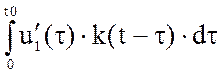 + [u2(t0)
– u1(t0)] k(t–t0) +
+ [u2(t0)
– u1(t0)] k(t–t0) +
+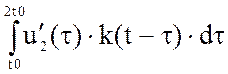 + [0–u2(2t0)] k(t–2t0) +
+ [0–u2(2t0)] k(t–2t0) + 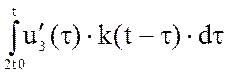 .
.
3. Определяем составляющие, которые входят в интеграл Дюамеля.
![]() =
= 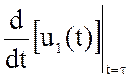 =
= 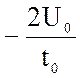
![]() =
= 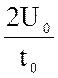
![]() = 0
= 0
k(t) = 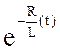
k(t–τ) = 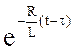
k(t–2t0) = 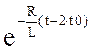
k(t–t0) = 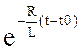
4. Определяем интегралы Дюамеля и записываем для каждого участка характеристики источника напряжения решения для напряжения uВЫХ(t).
В промежутке 0<t<t0:
uВЫХ1(t)= U0 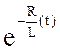 +
+ ![]()
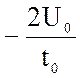
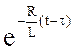 dτ
= .
dτ
= .
В промежутке t0<t<2t0:
uВЫХ2(t)= U0 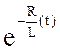 +
+ ![]()
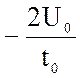
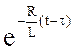 dτ +
0 +
dτ +
0 +![]()
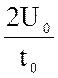
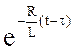 dτ = ,
dτ = ,
Для промежутка времени 2t0<t<![]() :
:
uВЫХ3(t) = U0 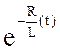 +
+ ![]()
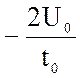
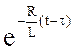 dτ +
0 +
dτ +
0 +![]()
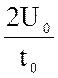
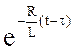 dτ –
dτ –
–U0 k(t–2t0) = 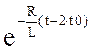 + 0.
+ 0.
Пример 2
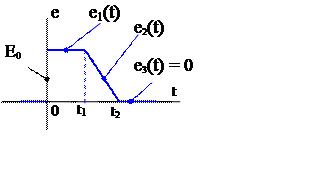
На вход цепи, рис. 3а, подключён источник ЭДС e(t). Заданы R1= 1 кОм, R1= 1 кОм, R2= 2 кОм, C = 0.5 мкФ и график источника ЭДС e(t), рис.3б , где E0 = 100 В, t1 = 10 мс, t2 = 30 мс.
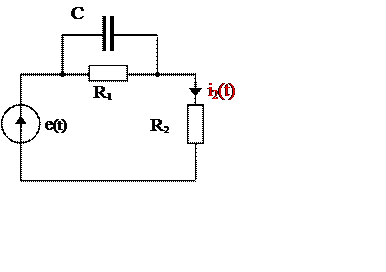 |
|||
 |
|||
а б
Рис. 3
Найти: закон изменения выходного напряжения i2(t)
Решение
1. Для тока i2(t) операторным методом рассчитываем переходную проводимость цепи g(t), как включение цепи на источник постоянной ЭДС 1 В.
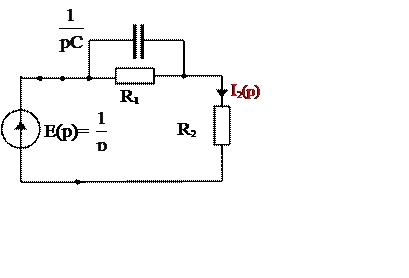 |
|||
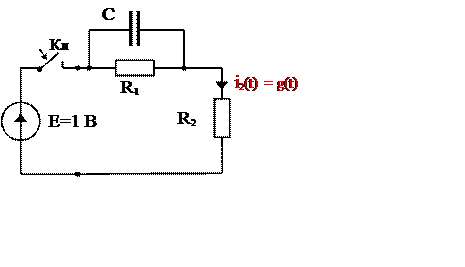 |
|||
а б
Рис. 4
· Операторная схема замещения приведена на рис. 4б.
Определим параметры схемы (см. табл. 2, раздел l 521)
e(t)=1
® Е(p) = ![]() ; UC(0) = 0 ® ЕC(p) =
; UC(0) = 0 ® ЕC(p) = 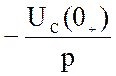 = 0
= 0
· По эквивалентной операторной схеме находится изображение напряжения. тока I2(p) по закону Ома:
I2(p) =  =
= 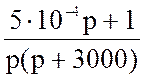
· По теореме разложения определяем оригинал напряжения uС(t).
I2(p) =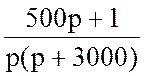 =
= 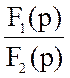
Корни F2(p) =0, p1= 0 c−1 и p2 = − 3000 c−1.
F¢2(p) =![]() ( p2 + p3000)=
2 p +3000.
( p2 + p3000)=
2 p +3000.
i2(t) = g(t) = 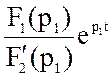 +
+ 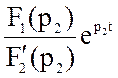 =
=
= 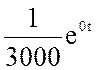 +
+
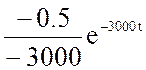 = 0.333 10-3 + 0.1667 10-3
= 0.333 10-3 + 0.1667 10-3![]() A.
A.
g(t) = 0.333 + 0.1667![]() мA.
мA.
2. Для трёх участков характеристики входного напряжения uВХ(t) источника (рис. 1б), имеющего аналитическое описание и представленного кусочно-гладкой функцией после коммутации, составим интеграл Дюамеля.
![]()
![]() u1(t) = U0, u1(t)
= 100,
u1(t) = U0, u1(t)
= 100,
uВХ(t) = u2(t) = a t + b, = u2(t) = – 5000 t + 150,
u3(t) = 0, u3(t) = 0,
a = 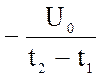 в =
в = 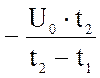
![]()
![]() u1(t) = a1 t + b1, u1(t)
=
u1(t) = a1 t + b1, u1(t)
= 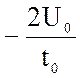 t
+ U0,
t
+ U0,
uВЫХ(t)= u2(t) = a2 t + b2, = u2(t)
= 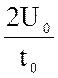 t
– 3 U0,
t
– 3 U0,
u3(t) = 0, u3(t) = 0,
· В промежутке 0<t<t0 можно воспользоваться уже имеющейся формулой (1):
uВЫХ(t)= u1(0) k(t) + 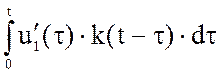 .
.
· В промежутке t0<t<2t0 следует учесть скачок напряжения e2(t1) – e1(t1), а также то, что напряжение изменяется по закону e2(t):
uВЫХ(t)= u1(0) k(t) + 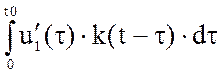 + [u2(t0) – u1(t0)]
k(t–t0) + +
+ [u2(t0) – u1(t0)]
k(t–t0) + +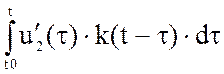 ,
,
где k(t–t1) учитывает запаздывание скачка [u2(t0) – u1(t0)] на время t0 по сравнению с началом отсчёта времени.
·
Для промежутка времени 2t0<t<![]() учитываем скачок - u2(2t0), а
также то, что u2(t)
действует лишь до 2t0:
учитываем скачок - u2(2t0), а
также то, что u2(t)
действует лишь до 2t0:
uВЫХ(t) = u1(0) k(t) + 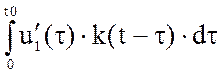 + [u2(t0) – u1(t0)]
k(t–t0) +
+ [u2(t0) – u1(t0)]
k(t–t0) +
+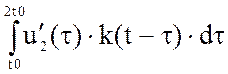 +
[0–u2(2t0)] k(t–2t0) +
+
[0–u2(2t0)] k(t–2t0) + 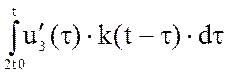 .
.
3. Определяем составляющие, которые входят в интеграл Дюамеля.
![]() =
= 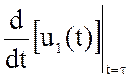 =
=
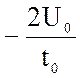
![]() =
= 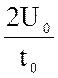
![]() = 0
= 0
k(t) = 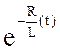
k(t–τ) = 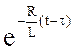
k(t–2t0) = 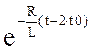
k(t–t0) = 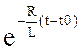
5. Определяем интегралы Дюамеля и записываем для каждого участка характеристики источника напряжения решения для напряжения uВЫХ(t).
В промежутке 0<t<t0:
uВЫХ(t)= U0 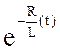 +
+ ![]()
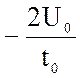
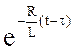 dτ = .
dτ = .
В промежутке t0<t<2t0:
uВЫХ(t)= U0 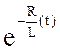 +
+ ![]()
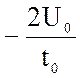
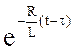 dτ + 0 +
dτ + 0 +![]()
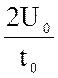
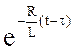 dτ = ,
dτ = ,
Для промежутка времени 2t0<t<![]() :
:
uВЫХ(t) = U0 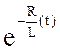 +
+ ![]()
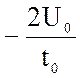
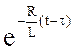 dτ + 0 +
dτ + 0 +![]()
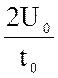
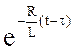 dτ –
dτ –
–U0 k(t–2t0) = 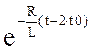 + 0.
+ 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.