L. 522. «Электротехника» Аксютин В.А.
Примеры расчета
переходных процессов в цепях первого порядка.
Пример 1.
|
Рис. 1
Решение
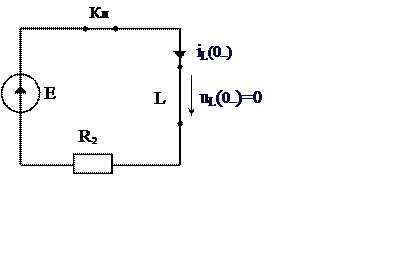1. Рассчитаем установившийся режим до
коммутации и определим независимые начальные значения iL(0–) = iL(0+).
 |
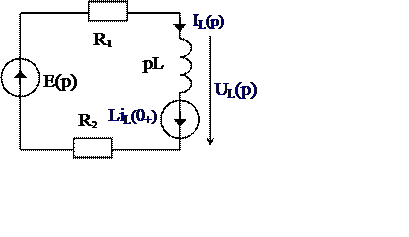а б
Рис. 2
До коммутации установившийся режим постоянного тока R1 отключено, индуктивное сопротивление равно нулю. Из схемы рис. 2а определим:
iL(0–) = E/ R2 = 15/20 = 0.75 A. iL(0+) = iL(0–) = 0.75 A.
2. Для режима после коммутации составим эквивалентную операторную схему рис. 2б. Определяем параметры схемы замещения:
Изображение постоянной ЭДС: Е(p) = 
= 
.
Операторная ЭДС индуктивности: L iL(0+) = 0.25 0.75=0.1875
3. По эквивалентной операторной схеме находится изображение тока IL(p) и напряжений. UL(p)
По второму закону Кирхгофа:
+
L iL(0+)
= IL(p)
(R1 + R1 + pL )
Определим изображение тока:
IL(p) =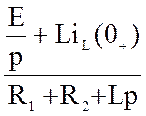 
= 
=
= = 
= 
.
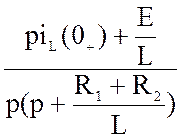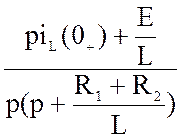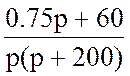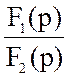Определим изображение напряжения:
UL(p) = Lp I(p) –L iL(0+) = Lp 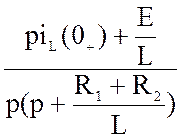–L iL(0+)
=
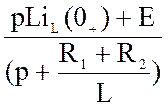– L iL(0+) = 
= 
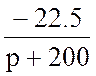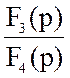
4. По теореме разложения определяем оригиналы тока iL(t) и напряжения uL(t).
IL(p) = =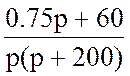
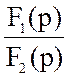
Корни F2(p) =0, p1= 0 c−1 и p2= − 200 c−1.
F¢2(p) =
( p2 + p200
)= 2 p +200.
iL(t) =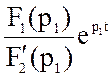 
+
= 
+
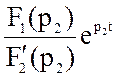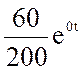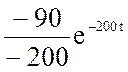= 0.3 + 0.45
A.
UL(p) = = .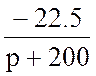
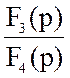Корень уравнения F4(p) =0, p3= − 200 c−1.и
F¢4(p) =( p +
200 )= 1.
uL(t) =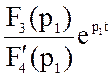
= 
=−
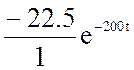22.5 B.
iL(t) = 0.3 +
0.45 A. и uL(t) =− 22.5 B.
Пример 2.
 |
|||
|
|||
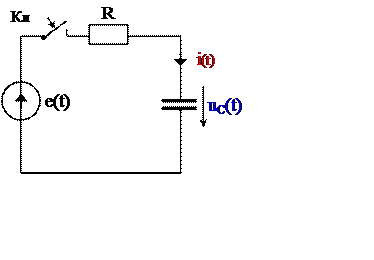Рис. 3
Решение
1. До коммутации ключ разомкнут, в цепи ток равен нулю ёмкость заряжена и имеет значение uC(0–) = uC(0+).= – 50 В
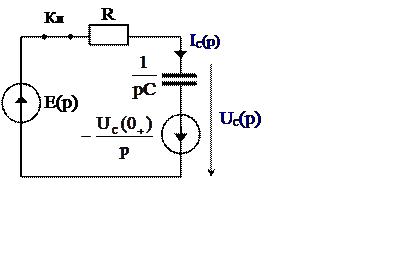2. Для после коммутационного режима составим
эквивалентную операторную схему.
Рис. 4
Определим параметры схемы (см. табл. 2, раздел l 521)
e(t)=120e–4t ® Е(p) =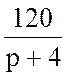 
; 
= 
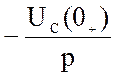3. По эквивалентной операторной схеме находится изображение напряжения. UС(p)
Составляем уравнение по второму закону Кирхгофа:
Е(p) 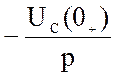= IC(p) (R + 
)
Определяем изображение тока:
IC(p) =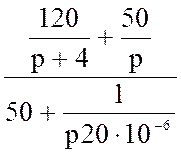 
= 
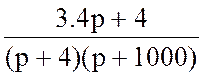
Находим изображение напряжения на ёмкости:
UC(p) = IC(p) +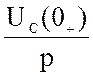
= 
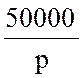IC(p) +
= 
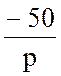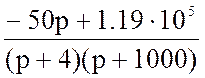
4. По теореме разложения определяем оригинал напряжения uС(t).
UC(p) = =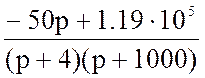
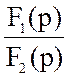
Корни F2(p) =0, p1= − 4 c−1 и p2 = − 1000 c−1.
F¢2(p) =( p2 + p1004+4000 )= 2
p
+1004.
uC(t) = + =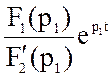
= 
+ 
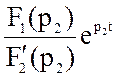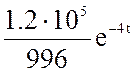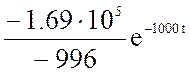= 120 
− 170
A.
Пример 3.
 |
|||
|
|||
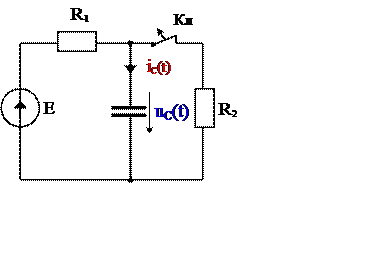Рис. 5
Решение
1. Рассчитаем установившийся режим до коммутации, схема рис. 6а, Определим независимые начальные значения uC(0–) = uC(0+).
 |
|||
 |
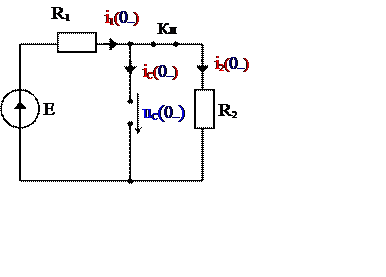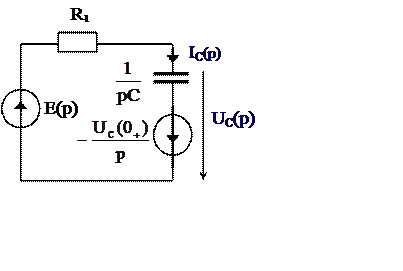а б
Рис. 6
i1(0–)
= i2(0–) =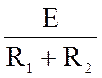 
= 1 A.
uC(0–) = uC(0+) = i2(0–) R2 = 20 B.
2. Для после коммутационного режима составим эквивалентную операторную схему рис. 6б.
Определим параметры схемы (см. табл. 2, раздел l 521)
Е(p) =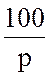 
; = 
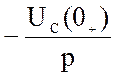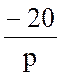
3. По эквивалентной операторной схеме находится изображение тока IС(p)
Составляем уравнение по второму закону Кирхгофа:
Е(p) 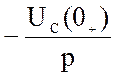= IC(p) (R + )
Определяем изображение тока:
IC(p) =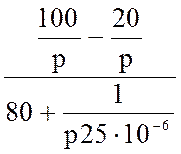 
= 
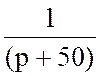
4. По справочным данным (табл. 1 раздел l 521) определяем оригинал напряжения uС(t).
IC(p) = 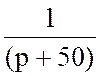¬ iС(t) =1 
A.
Пример 4.
 |
|||
|
|||
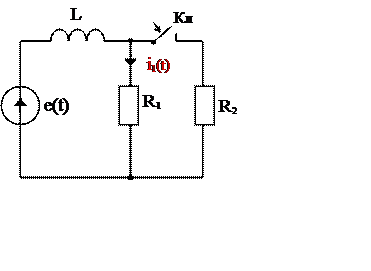Рис. 7
Решение
1. Рассчитаем установившийся режим до коммутации и определим независимые начальные значения iL(0–) = iL(0+).
 |
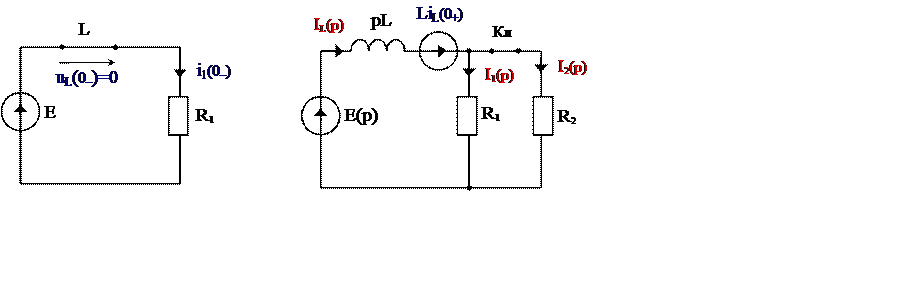а б
Рис. 8
iL(0–) = iL(0+) = 
= 0.24 A.
2. Для после коммутационного режима составим эквивалентную операторную схему.
Определим параметры схемы (см. табл. 2, раздел l 521)
Е(p) = 
; LiL(0+) =0.048 A/c.
3. По эквивалентной операторной схеме находится изображение тока IL(p).
Составляем уравнение по второму закону Кирхгофа:
Е(p) + L iL(0+) = IL(p) (R + p L)
где R=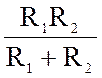
= 14.29 Ом.
Определяем изображение тока:
IL(p) =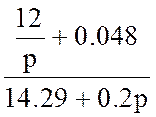 
= 
.
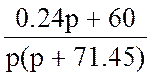4. По теореме разложения определяем оригиналы тока iL(t) и затем по правилу рычага определяем ток в i1(t) .
IL(p) = =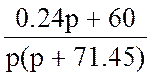
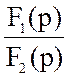
Корни F2(p) =0, p1= 0 c−1 и p2= − 71.45 c−1.
F¢2(p) =( p2 + p71.45 )= 2 p +71.45.
iL(t) = + =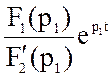
= 
+
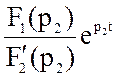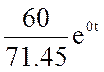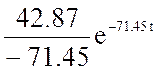= 0.84 − 0.6
A.
i1(t) = iL(t)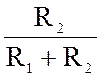 
=
0.24 − 0.171 A.
i1(t) = 0.24 − 0.171 A.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
