Применение метода наложения к расчету электрических цепей с двумя и более источниками энергии. Метод узловых потенциалов (узловых напряжений) (главы 3-5 учебного пособия "Теоретические основы электротехники в примерах и задачах")

3. ПРИМЕНЕНИЕ МЕТОДА НАЛОЖЕНИЯ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ДВУМЯ И БОЛЕЕ ИСТОЧНИКАМИ ЭНЕРГИИ

Если цепь имеет несколько источников энергии, то для расчета цепи можно применить метод наложения. Этот метод использует принцип независимости действия источников. Использование принципа наложения дает возможность заменить вычисления сложных цепей несколькими относительно простыми цепями, в каждой из которых действует один источник энергии.

Задача 3.1.

Методом наложения определить токи во всех ветвях цепи, схема которой приведена на рис. 3.1, если задано , , , , .

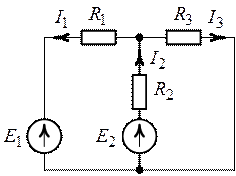
Рис. 3.1.

Решение.

1. Произвольно выбираем положительные направления токов в ветвях цепи (рис. 3.1). Определяем частичные токи от действия каждого источника в отдельности.

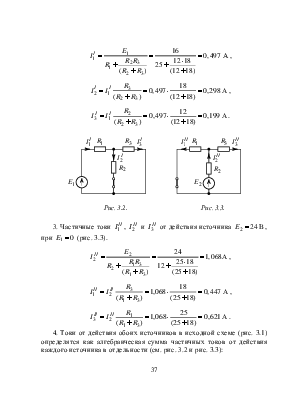
2. Частичные токи ,  и  от действия источника , при  (рис. 3.2).

,

,

.

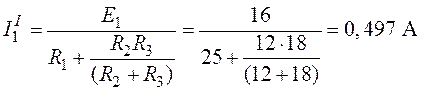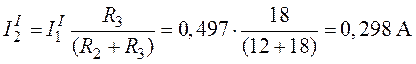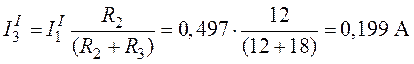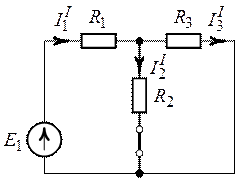
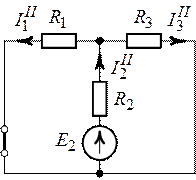
            Рис. 3.2.                                            Рис. 3.3.

3. Частичные токи ,  и  от действия источника , при  (рис. 3.3).

,

,

.

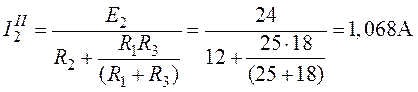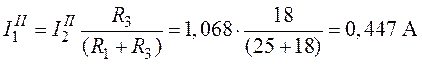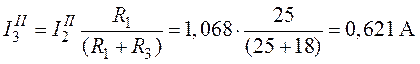4. Токи от действия обоих источников в исходной схеме (рис. 3.1) определятся как алгебраическая сумма частичных токов от действия каждого источника в отдельности (см. рис. 3.2 и рис. 3.3):

;

;

.

П р и м е ч а н и е:  частичный ток, совпадающий по направлению с искомым (рис. 3.1), считается положительным, а несовпадающий – отрицательным. Отрицательное значение тока  указывает на то, что направление тока противоположно указанному на рис. 3.1.

Задача 3.2.

Используя метод наложения определить токи во всех ветвях цепи , рис. 3.4, если задано , ,  , , , .

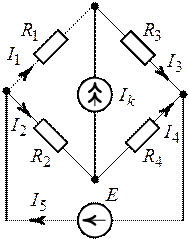
Рис. 3.4.                                            Рис. 3.5.

Решение.

1. Принимаем за положительные  направления токов в ветвях цепи направления, указанные на рис. 3.4.

2. Определяем частичные токи  от действия источника ЭДС , при  (рис. 3.5):

;

;

.

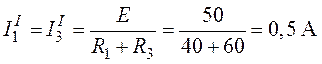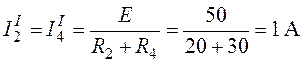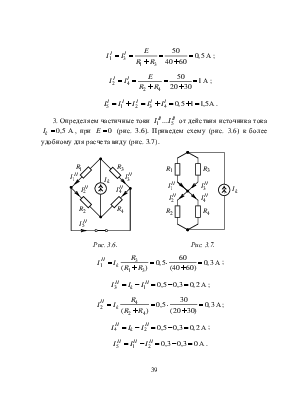
3. Определяем частичные токи  от действия источника тока , при  (рис. 3.6). Приведем схему (рис. 3.6) к более удобному для расчета виду (рис. 3.7).

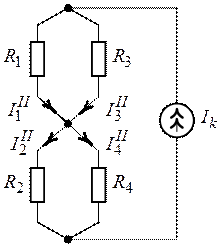
Рис. 3.6.                                            Рис. 3.7.

;

;

;

;

.

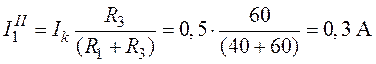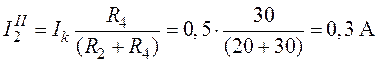4. Токи в исходной схеме (рис. 3.4) от действия обоих источников определим, как алгебраическую сумму частичных токов (см.  рис. 3.5  и  рис. 3.6)

;

;

;

;

.

Задачи для самостоятельного решения

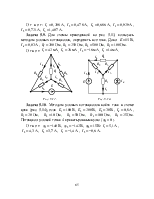
Задача 3.3. Методом наложения определить токи в цепи (рис. 3.8), если задано , , , , .

О т в е т: , .

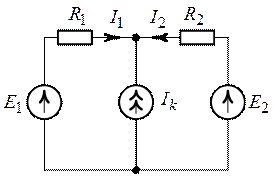
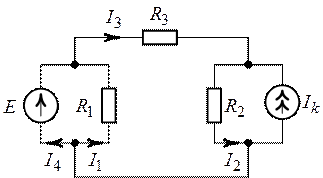
Рис. 3.8.                                              Рис. 3.9.

Задача 3.4. Методом наложения определить все токи в цепи, схема которой приведена на рис. 3.9. Параметры элементов цепи заданы , , .

О т в е т: , , , .

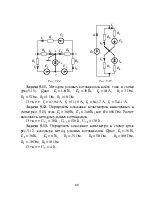
Задача 3.5. В схеме (рис. 3.10) методом наложения определить все токи, если , , , , , .

О т в е т: , , , , ,      

.

Задача 3.6. Для схемы цепи рис. 3.11 используя метод наложения определить все токи, если , , , , , .

О т в е т: , , , ,

.

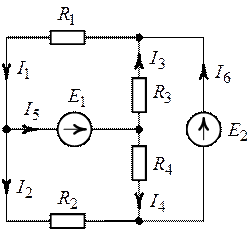
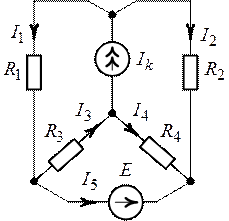
Рис. 3.10.                                                  Рис. 3.11.

Задача 3.7. Используя метод наложения рассчитать токи в схеме цепи рис. 3.12, если , , ,  , , , .

О т в е т: , , , ,

.

Задача 3.8. Методом наложения определить токи в ветвях цепи (рис. 3.13) содержащих резистивные сопротивления. Дано , , , , , .

О т в е т: , , .

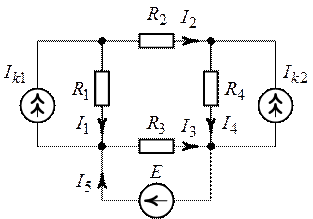
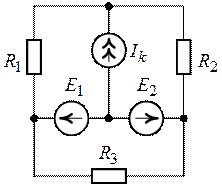
          Рис. 3.12.                                            Рис. 3.13.

4. МЕТОД КОНТУРНЫХ ТОКОВ

Задачу расчета разветвленных цепей можно значительно упростить, если воспользоваться специальными методами расчета сложных цепей. Одним из этих методов является метод контурных токов. Метод контурных токов можно определить как метод расчета, в котором за неизвестные принимаются токи контуров. Использование метода позволяет сократить количество составляемых уравнений по отношению к расчету при непосредственном применении законов Кирхгофа.

Задача 4.1.

Методом контурных токов рассчитать все токи в ветвях схемы (рис. 4.1). Даны: , , , , , , , , , . Выполнить проверку решения по второму закону Кирхгофа.

Решение.

1. Цепь (рис. 4.1) содержит шесть ветвей (), четыре узла (), источники тока в цепи отсутствуют ().

Зададим произвольное положительное направление токов в ветвях схемы и обозначим их как указано на рис. 4.2.

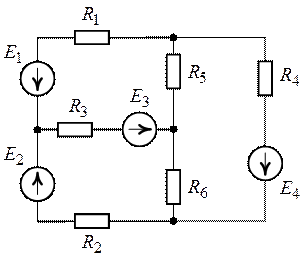
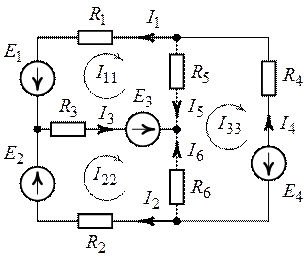
Рис. 4.1.                                               Рис. 4.2.

2. Определим достаточное количество уравнений для расчета цепи по методу контурных токов:

.

Достаточное количество контурных уравнений равно трем.  Выделим в схеме три независимых контура, по которым замкнем контурные токи ,  и  (рис. 4.2). Направление действия контурных токов выберем по часовой стрелке. Положительное направление обхода контура совместим с направлением контурного тока.

3. Система контурных уравнений (уравнений по второму закону Кирхгофа) имеет вид (рис. 4.2):

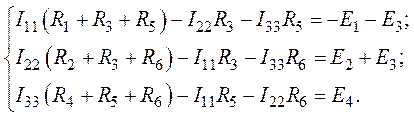
4. Выполним подстановку числовых значений

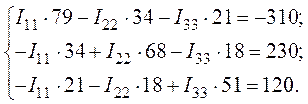
5. Решение полученной системы уравнений выполним с помощью определителей по методу Крамера:

,   ,   .

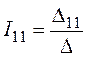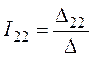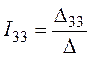Главный определитель системы:

 .

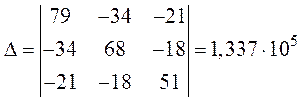Дополнительные определители:

  ,

,

.

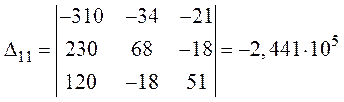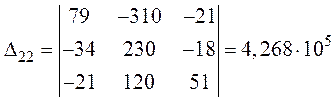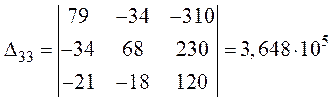6. Контурные токи

,

,

.

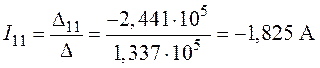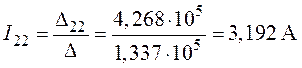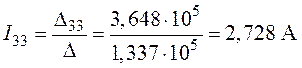7. Действительные токи в ветвях схемы (рис. 4.2) определим как алгебраическую сумму контурных токов смежных контуров:

;

;

;

;

,

8. Проверку расчета выполним, составив уравнение по второму закону Кирхгофа, например, для внешнего контура (рис. 4.2). Направление обхода контура по часовой стрелке

.

Подставляя в уравнение числовые значения, получим:

,

.

Задача 4.2.

Для схемы, рис. 4.3, пользуясь методом контурных токов, определить все токи, если , , ,  , , ,  .

Решение.

1. Схема (рис. 4.3) содержит шесть ветвей (), четыре узла (), один источник тока  ().

Положительные направления токов в ветвях схемы обозначим в соответствии с рис. 4.4.

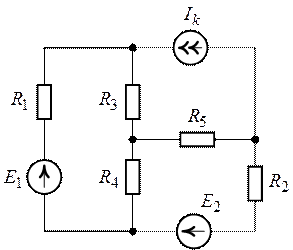
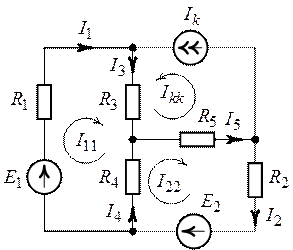
Рис. 4.3.                                              Рис. 4.4.

2. Достаточное количество уравнений для расчета цепи по методу контурных токов равно двум:

.

Независимые контура и направления протекания контурных токов,  обозначены на рис. 4.4.

Для ветви с источником тока  создадим третий контур с контурным током  по направлению, совпадающему с направлением источника (рис. 4.4).

Считаем, что  является известным контурным током, который будем учитывать только при составлении уравнений независимых контуров.

3. Система уравнений, составленная по методу контурных токов, будет иметь вид:

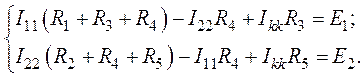
4. После подстановки числовых значений параметров цепи получим:

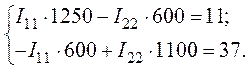
5. Решение системы позволяет получить значения контурных токов

,  .

6. Действительные токи в ветвях (рис.4.4) находим как алгебраическую сумму контурных токов смежных контуров

;

;

;

;

.

Задача 4.3.

Требуется  рассчитать токи в ветвях цепи (рис. 4.5), если , , , , , , , , ,, . Расчеты выполнить методом контурных токов.

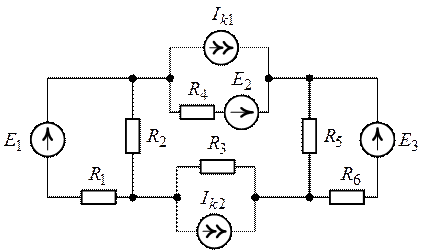
Рис. 4.5.

Решение.

1. Преобразуем цепь (рис. 4.5) к виду более удобному для расчета, объединив в один узел  узлы равного потенциала (рис. 4.6).

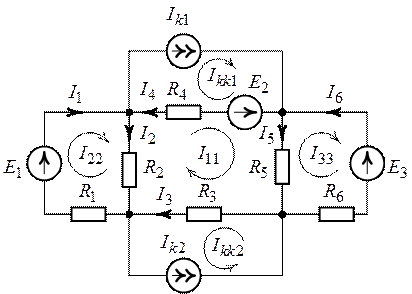
Рис. 4.6.

Цепь (рис. 4.6) содержит восемь ветвей (), четыре узла  (), два источника тока ,  ().

Зададимся произвольным положительным направлением токов в ветвях схемы и обозначим их как указано на рис. 4.6.

2. Определим достаточное количество уравнений, которое равно трем

.

Выделим в схеме три независимых контура, по которым замкнем контурные токи ,  и .

Направление контурных токов выберем по часовой стрелке. Для ветвей с источниками тока создадим два дополнительных контура с контурным током , . Направления дополнительных контурных токов выберем так, чтобы они совпадали с направлениями действия источников тока  и .

3. Система контурных уравнений, записанных по  второму закону Кирхгофа относительно неизвестных контурных токов, имеет вид

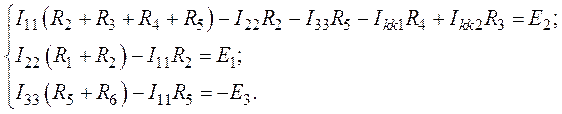
4. Приведем систему к матричной форме

.

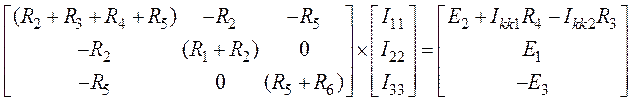5. Подставив числовые значения параметров элементов цепи, получим

.

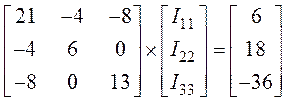6. Решение матричной системы позволяет определить контурные токи

,  , .

7. Определяем действительные токи в ветвях схемы (рис. 4.6)

;

;

;

;

;

.

Задачи для самостоятельного решения

Задача 4.4. Для цепи изображенной на рис. 4.7, требуется определить контурные токи, указные на схеме, если , , , , , , , .

О т в е т: ,  .

Задача 4.5. Требуется рассчитать контурные токи, указные на схеме (рис.4.8), если , , , , .