О т в е т: ![]() ,
, ![]() .
.
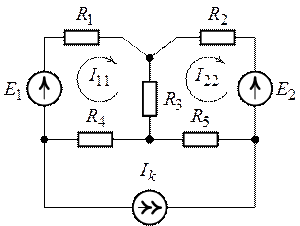
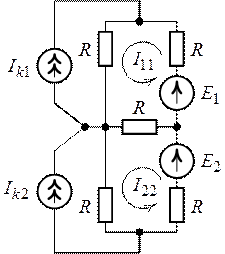
Рис. 4.7. Рис. 4.8.
Задача 4.6. Методом
контурных токов определить токи в ветвях цепи (рис. 4.9).Дано: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Положительные направления токов
указаны на схеме.
. Положительные направления токов
указаны на схеме.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
Задача 4.7. Методом
контурных токов определить токи в ветвях цепи (рис. 4.10), если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() .
.
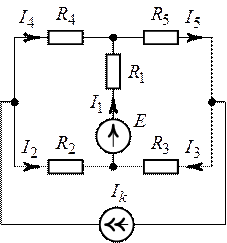
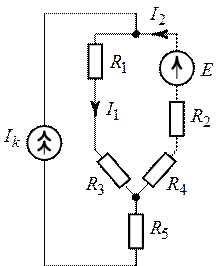
Рис. 4.9. Рис. 4.10.
Задача 4.8. Методом
контурных токов определить показания амперметров установленных в ветвях цепи, схема
которой приведена на рис.4.11. Дано: ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() .
.
Задача 4.9. Методом
контурных токов рассчитать указанные в схеме (рис. 4.12) токи, если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
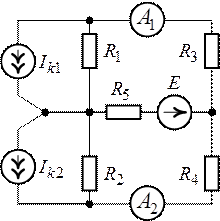
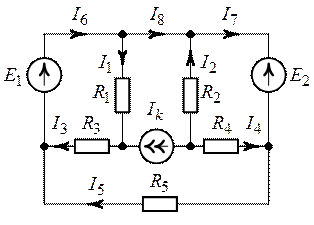
Рис. 4.11. Рис. 4.12.
5. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ (УЗЛОВЫХ НАПРЯЖЕНИЙ)
Метод узловых потенциалов это метод расчета электрических цепей, в котором за неизвестные принимаются потенциалы (напряжения) узлов схемы. Использование метода позволяет сократить количество составляемых уравнений по отношению к расчету при непосредственном применении законов Кирхгофа.
Задача 5.1.
Определить токи в ветвях цепи (рис. 5.1) методом
узловых потенциалов, если ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
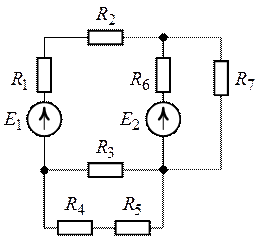
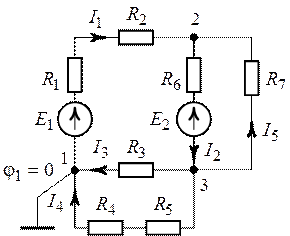
Рис. 5.1. Рис. 5.2.
Решение
1. Схема (рис. 5.1) содержит пять ветвей (![]() ), три узла (
), три узла (![]() ).
).
2. Достаточное количество уравнений для расчета цепи по методу узловых потенциалов определяется числом уравнений по первому закону Кирхгофа и равно двум:
![]() .
.
Примем потенциал одного из узлов, например узла 1
(рис.5.2), равным нулю (![]() ).
).
3. Расчетные уравнения для определения потенциалов ![]() и
и ![]()
(узел 2, 3) будут иметь вид:
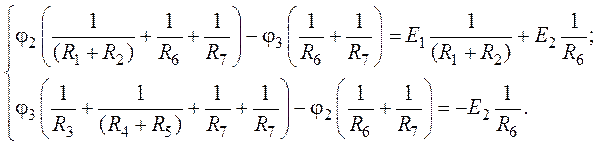
4. После подстановки в систему числовых значений имеем
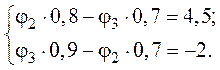
5. Решая систему относительно неизвестных потенциалов ![]() и
и ![]() ,
находим
,
находим
![]() ,
, ![]() .
.
6. Зададим произвольное направление токов в ветвях схемы (рис.5.2). По закону Ома для участка цепи, считая, что ток направлен от узла с большим потенциалом к узлу с меньшим потенциалом, выражаем токи:
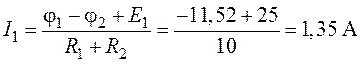 ;
;
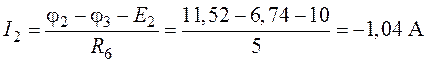 ;
;
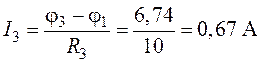 ;
;
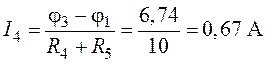 ;
;
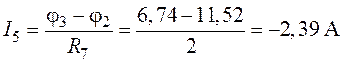 .
.
7. Проверка решения. Проверку решения выполним, составив уравнение по второму закону Кирхгофа для внешнего контура:
![]() .
.
Подставляя числовые значения в уравнение, получим:
![]()
![]() .
.
Задача 5.2.
Для схемы, представленной на рис. 5.3, пользуясь
методом узловых потенциалов, определить все токи. Дано: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
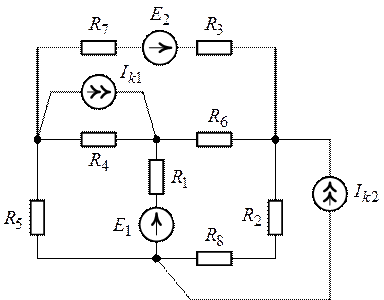
Рис. 5.3.
Решение.
1. Схема (рис. 5.3) содержит восемь ветвей (![]() ), из которых шесть ветвей с
неизвестными токами, четыре узла (
), из которых шесть ветвей с
неизвестными токами, четыре узла (![]() ), две ветви с
источниками тока (
), две ветви с
источниками тока (![]() ).
).
2. Достаточное количество уравнений для расчета цепи равно трем
![]() .
.
Потенциал узла 1 (рис. 5.4) примем равным нулю (![]() ).
).
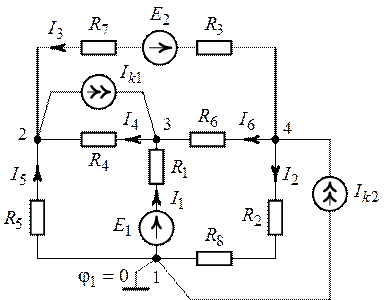
Рис. 5.4.
3. Система уравнений для определения потенциалов ![]() ,
, ![]() и
и
![]() (узлы 2, 3 и 4) согласно рис. 5.4
будет иметь вид:
(узлы 2, 3 и 4) согласно рис. 5.4
будет иметь вид:
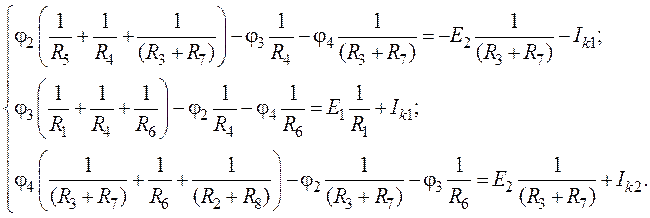
4. Для расчета приведем систему к матричной форме:
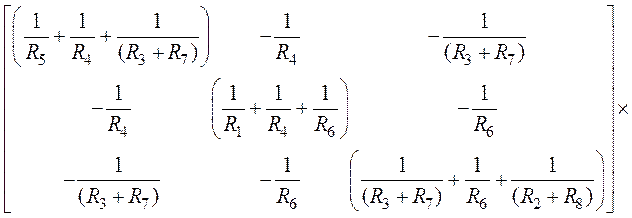
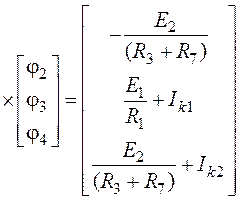 .
.
5. После подстановки числовых значений получим
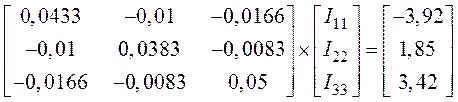 .
.
6. Решением матричного уравнения будут потенциалы узлов
![]() ;
; ![]() ;
; ![]() .
.
7. Зададим направление токов в ветвях схемы, как указано на рис. 5.4 и выразим токи:
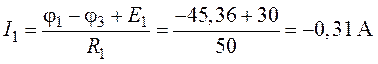 ;
;
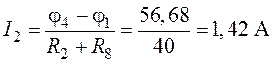 ;
;
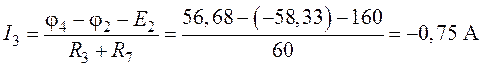 ;
;
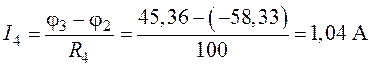 ;
;
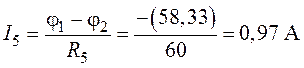 ;
;
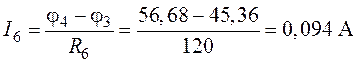 .
.
8. Проверка решения. Проверку решения выполним по первому закону Кирхгофа, например, для узла 1:
![]() .
.
Задача 5.3.
Методом узловых потенциалов определить токи во всех
ветвях схемы, изображенной на рис. 5.5. Заданы ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
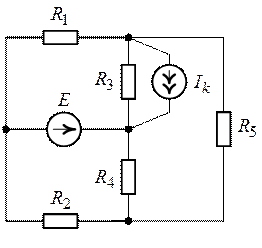
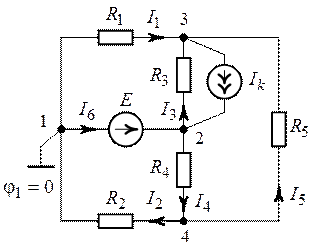
Рис. 5.5. Рис. 5.6.
Решение.
1. Схема (рис. 5.5) содержит семь ветвей (![]() ), четыре узла (
), четыре узла (![]() ), одна ветвь с источником тока (
), одна ветвь с источником тока (![]() )
)
В цепи имеется ветвь с источником ЭДС ![]() , не содержащая сопротивления (
, не содержащая сопротивления (![]() ) т.е. с нулевым сопротивлением.
) т.е. с нулевым сопротивлением.
2. Общее число уравнений для расчета цепи по методу узловых потенциалов при наличии ветви с источником ЭДС, не содержащей сопротивления, равно двум
![]() .
.
Примем потенциал узла 1 (рис. 5.6) равным нулю (![]() ).
).
П р и м е ч а н и е: Целесообразно принять равным нулю потенциал одной из узловых точек ветви с источником ЭДС с нулевым сопротивлением.
Тогда потенциал узла 2 имеет значение напряжения,
равное ![]() , т.е.
, т.е. ![]() (рис.
5.6).
(рис.
5.6).
3. Расчетные уравнения для потенциалов оставшихся узловых точек (узлы 3, 4) будут иметь следующий вид:
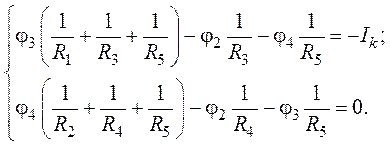
4. Подставив в систему числовые значения, получим
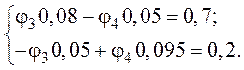
5. Решение системы относительно неизвестных потенциалов позволяет получить
![]() ,
, ![]() .
.
6. Зададим направления токов в ветвях цепи, как указано на рис.5.6. По закону Ома выразим токи:
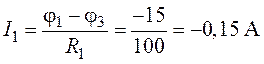 ;
;
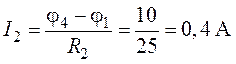 ;
;
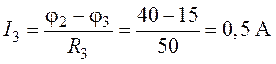 ;
;
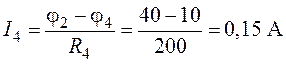 ;
;
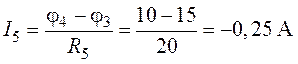 .
.
Ток ![]() в ветви с источником
в ветви с источником
![]() найдем по первому закону Кирхгофа
для узла 1 (рис. 5.6):
найдем по первому закону Кирхгофа
для узла 1 (рис. 5.6):
![]() .
.
7. Проверка решения. По второму закону Кирхгофа для внешнего контура цепи (рис. 5.6) запишем:
![]() .
.
После подстановки числовых значений получим:
![]() .
.
Задача 5.4.
Вычислить токи в
ветвях схемы, рис. 5.7, методом узловых потенциалов,
если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
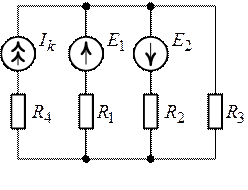
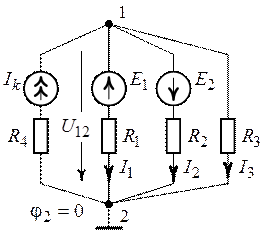
Рис. 5.7. Рис. 5.8.
Решение.
1. Схема (рис.5.7) содержит четыре ветви (![]() ), два узла (
), два узла (![]() ),
одна ветвь с источником тока (
),
одна ветвь с источником тока (![]() ).
).
Рассматривая частный случай схемы с двумя узлами, воспользуемся для расчета методом двух узлов.
2. Потенциал узла 2 (рис. 5.8) примем равным нулю (![]() ). Тогда напряжение между узлами 1
и 2 найдем как
). Тогда напряжение между узлами 1
и 2 найдем как
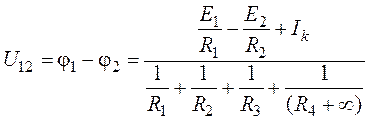
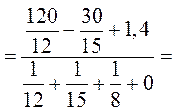
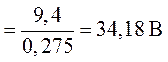 .
.
3. Направление токов в ветвях цепи зададим в соответствии с указанными на рис. 5.8, тогда
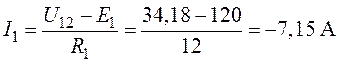 ;
;
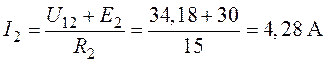 ;
;
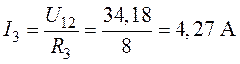 .
.
7. Проверка решения. По первому закону Кирхгофа для узла 2 запишем:
![]() .
.
Задача 5.5.
Определить показание вольтметра установленного в схеме
(рис.5.9), если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Внутреннее сопротивление вольтметра принять равным
.
Внутреннее сопротивление вольтметра принять равным ![]() .
Расчет цепи выполнить по методу узловых потенциалов.
.
Расчет цепи выполнить по методу узловых потенциалов.
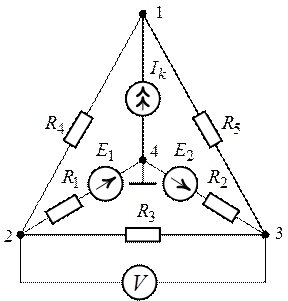
Рис. 5.9.
Решение.
Показание вольтметра определим, как разность потенциалов
узловых точек 3 и 2 в местах его подключения: ![]() .
.
1. Определим потенциалы ![]() и
и
![]() узловых точек 2 и 3. Схема содержит
шесть ветвей (
узловых точек 2 и 3. Схема содержит
шесть ветвей (![]() ), четыре узла (
), четыре узла (![]() ), одна ветвь содержит источник тока (
), одна ветвь содержит источник тока (![]() ).
).
2. Достаточное количество уравнений для расчета цепи методом узловых потенциалов равно трем
![]() .
.
Потенциал узла 4 (рис. 5.9) примем равным нулю (![]() ).
).
3. Система уравнений для определения неизвестных
потенциалов ![]() ,
, ![]() и
и
![]() узловых точек 1, 2 и 3 будет иметь
вид:
узловых точек 1, 2 и 3 будет иметь
вид:
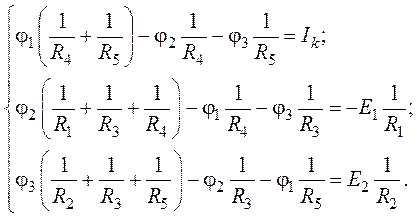
4. Приведем систему к матричной форме:
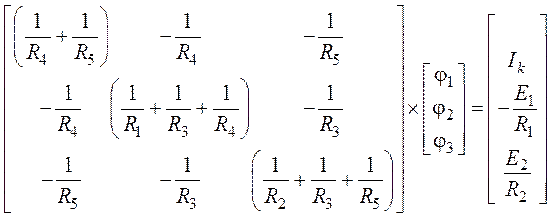 .
.
5. Подставив в систему числовые значения заданных параметров элементов цепи, получим:
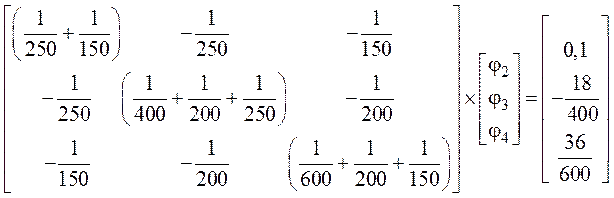 .
.
6. Из решения системы получим
![]() ,
, ![]() .
.
7. Показания вольтметра найдем как разность потенциалов узловых точек 3 и 2:
![]() .
.
Задачи для самостоятельного решения
Задача 5.6. Методом
узловых потенциалов рассчитать напряжения узловых точек, указанных на схеме
(рис. 5.10), и рассчитать все токи, если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Потенциал узловой точки 1 принять равным нулю (
.
Потенциал узловой точки 1 принять равным нулю (![]() ).
).
О т в е т: потенциалы узлов ![]() ,
,
![]() ,
, ![]() ;
;
токи
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Задача 5.7. Для
схемы (рис. 5.11), пользуясь методом узловых потенциалов, определить все токи. Дано
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
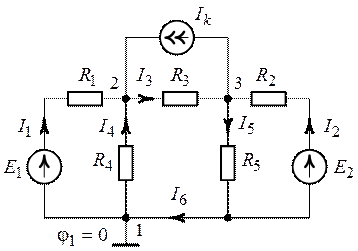
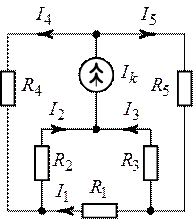
Рис. 5.10. Рис. 5.11.
Задача 5.8. Методом
узловых потенциалов найти токи в цепи, схема которой изображена на рис. 5.12,
если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Задача 5.9. Для
схемы приведенной на рис. 5.13, пользуясь методом узловых потенциалов,
определить все токи. Дано: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
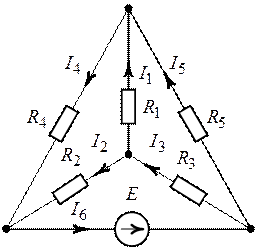
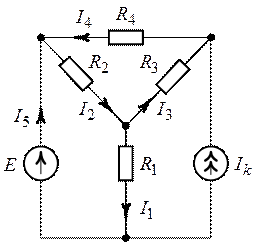
Рис. 5.12. Рис. 5.13.
Задача 5.10.
Методом узловых потенциалов найти токи в схеме цепи (рис. 5.14), если ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Потенциал узловой точки 4
принять равным нулю (
. Потенциал узловой точки 4
принять равным нулю (![]() ).
).
О т в е т: ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
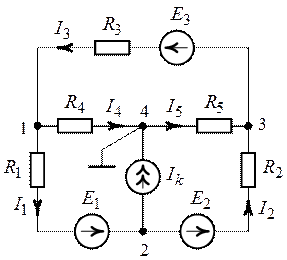
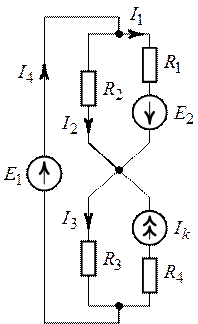
Рис. 5.14. Рис. 5.15.
Задача 5.11.
Методом узловых потенциалов найти токи в схеме (рис.5.15). Дано ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
О т в е т: ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Задача 5.12. Определить
показания вольтметров включенных в схеме рис. 5.16, если ![]() ,
, ![]() ,
все
,
все ![]() . Расчет
выполнить методом узловых потенциалов.
. Расчет
выполнить методом узловых потенциалов.
О т в е т: ![]() ,
, ![]() ,
, ![]() .
.
Задача 5.13. Определить
показание вольтметра в схеме цепи рис.5.17, используя метод узловых
потенциалов. Дано: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
О т в е т: ![]() .
.
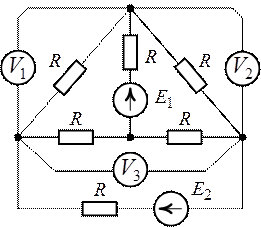
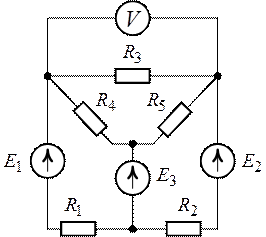
Рис. 5.16. Рис. 5.17.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.