
1.1 В евклидовом пространстве ![]()
![]() найдите
найдите
1) скалярное произведение векторов a, b;
2) угол между векторами a и b;
где ![]() =(1,1,1,1),
=(1,1,1,1),
![]() =(3,5,1,1).
=(3,5,1,1).
1.2 Найдите нормированный вектор
евклидова пространства ![]() , ортогональный векторам
, ортогональный векторам ![]() =(1,1,1),
=(1,1,1), ![]() =(1,-1,1).
=(1,-1,1).
1.3 Применяя процесс
ортогонализации Грамма-Шмидта, по заданному базису ![]() =(1,1,1),
=(1,1,1),
![]() =(1,2,3),
=(1,2,3), ![]() =(1,1,2)
евклидова пространства
=(1,1,2)
евклидова пространства ![]() постройте ортонормированный базис.
Сделайте проверку.
постройте ортонормированный базис.
Сделайте проверку.
1.4 Дополните до
ортонормированного базиса евклидова пространства ![]() систему векторов
систему векторов ![]() =(1,-2,2,-3),
=(1,-2,2,-3), ![]() =(2,-3,2,4).
=(2,-3,2,4).
2.1 В ортонормированном базисе
евклидова пространства ![]() линейный оператор задан
матрицей
линейный оператор задан
матрицей 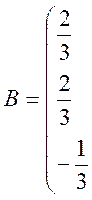
![]()
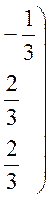 .
.
Будет ли этот оператор ортогональным?
2.2 Для данной матрицы 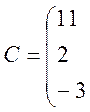
![]()
![]() найдите такую ортогональную матрицу
Т, что ТСТ-1 —диагональная матрица. Сделайте проверку.
найдите такую ортогональную матрицу
Т, что ТСТ-1 —диагональная матрица. Сделайте проверку.
2.3 Найдите собственные значения
и ортонормированный базис ![]() ,
, ![]() из собственных векторов
самосопряжённого линейного оператора
из собственных векторов
самосопряжённого линейного оператора ![]() , заданного в
некотором ортонормированном базисе
, заданного в
некотором ортонормированном базисе ![]() ,
, ![]() матрицей
матрицей 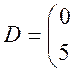
![]() . Найдите матрицу оператора
. Найдите матрицу оператора ![]() в базисе
в базисе ![]() ,
,
![]() .
.
2.4 Методом Лагранжа приведите
квадратичные формы ![]() , и
, и ![]() к каноническому виду. Укажите
невырожденное линейное преобразование переменных, приводящее к этому виду.
Сделайте проверку.
к каноническому виду. Укажите
невырожденное линейное преобразование переменных, приводящее к этому виду.
Сделайте проверку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.