Метод эквивалентного генератора для расчета сложных цепей с одним нелинейным элементом

L. 623. «Электротехника»                                                                                   Аксютин В.А.

Метод эквивалентного генератора для расчета сложных цепей с одним нелинейным элементом.

Метод эквивалентного генератора можно применить для определения токов в цепи с одним нелинейным элементом. Расчёт проводится в следующем порядке:

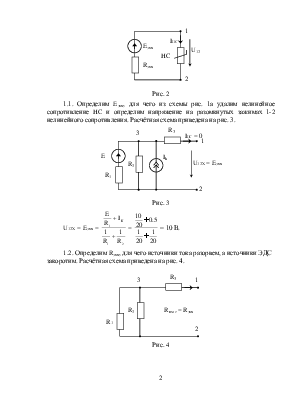
·  линейная часть цепи, не содержащая нелинейный элемент, представляется эквивалентным генератором рис. 2.

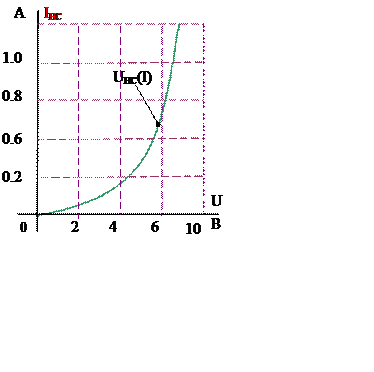
·  в одной системе координат строятся линейная ВАХ эквивалентного генератора U₁₂(I)= E_ЭКВ - I R_экв и ВАХ нелинейного элемента U_HC(I); в точке пересечения построенных ВАХ,  определяются напряжение и ток в нелинейном сопротивлении U₁₂ и I_НЭ.

·  остальные токи рассчитываются с использованием законов Кирхгофа или иных методов расчета линейных цепей, считая сопротивление нелинейного элемента постоянным R_НЭ= U₁₂ ∕ I_НC. или заменяя его источником ЭДС (E=U₁₂) или источником тока (J=I_НC).

Пример 1.

В цепи с нелинейным элементом НЭ рис. 1а. определить токи во всех ветвях.

Значения элементов цепи:   E = 10 B; I_k= 0.5 A; R₁ = 20 Ом; R₂ = 20 Ом; R₃ = 10 Ом; вольт-амперная характеристика НЭ приведена на рис 1б

 

а                                                                                               б

Рис. 1

Решение

1. Линейную часть цепи (рис 1, а), относительно зажимов нелинейного элемента, представляем эквивалентным генератором рис. 2

 

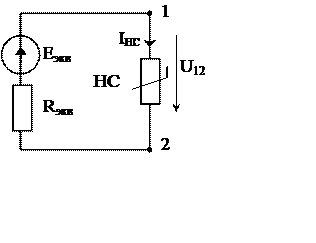Рис. 2

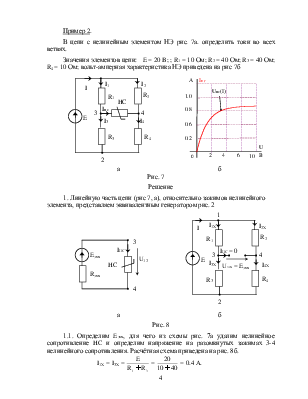
1.1. Определим E_экв, для чего из схемы рис. 1а удалим нелинейное сопротивление HC и определим напряжение на разомкнутых зажимах 1-2 нелинейного сопротивления. Расчётная схема приведена на рис. 3.

 

Рис. 3

U_12X = E_экв  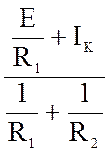=  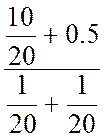=  = 10 В.

1.2. Определим R_экв, для чего источники тока разорвем, а источники ЭДС закоротим. Расчётная схема приведена на рис. 4.

 

Рис. 4

R_BX12 = R_экв = 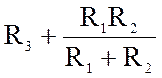 =  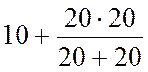= 20 Ом.

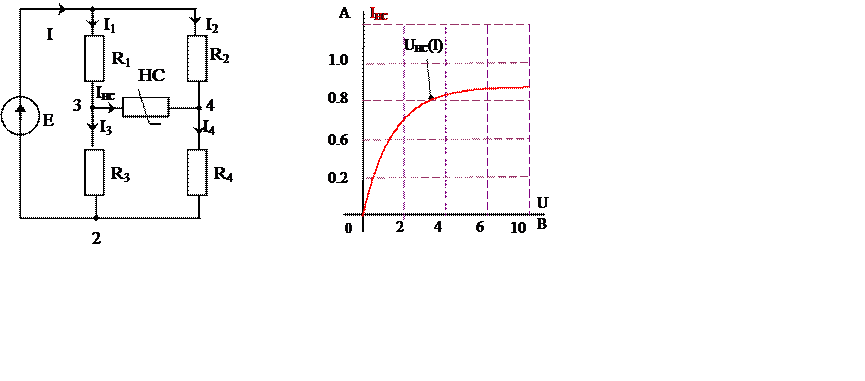
2. В одной системе координат строим линейную ВАХ эквивалентного генератора U₁₂(I)= E_ЭКВ - I·R_экв (U₁₂(I)= 10 - I·20) и ВАХ нелинейного элемента U_HC(I) (рис. 1б); в точке «а» (рис 5) пересечения построенных ВАХ,  определяются напряжение и ток в нелинейном сопротивлении U_НС и I_НС.

 

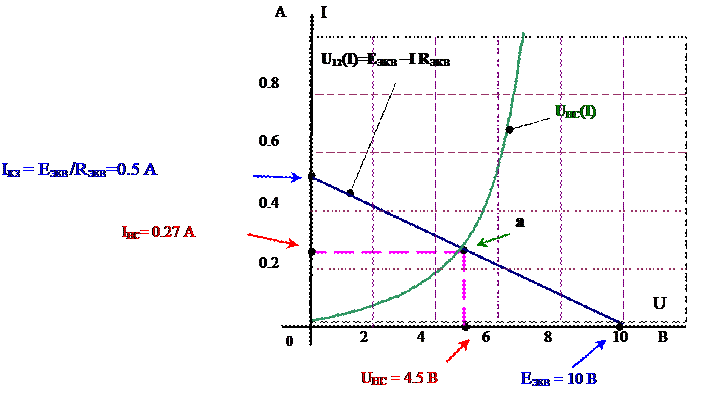Рис. 5

3. Остальные токи цепи (рис. 6) определим из системы уравнений (1), составленной по законам Кирхгофа, считая известными I_НС= 0.27 А и U_HC = 4.5 В.

 

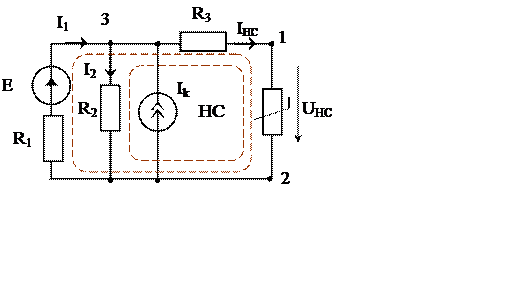Рис. 6

I₁ – I₂  +  I_k –  I_HC = 0;                      I₁ – I₂  +  0.5 –  0.27 = 0;

I₁ R₁ + I_HC R₃ + U_НС = E;         =      I₁ 20 + 0.27 10 + 4.5 = 10;                                                        (1)

 – I₂ R₂ + I_HC R₃ + U_НС = 0;           – I₂ 20 + 0.27 10  + 4.5 = 0;

Решая систему (1) получим токи:        I₁ = 0.14 A;        I₂ = 0.36 A;

Пример 2.

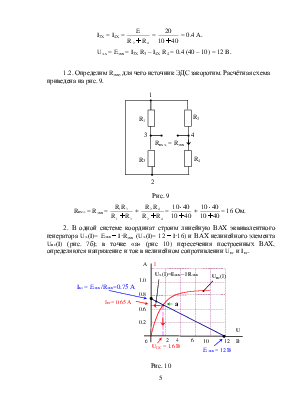
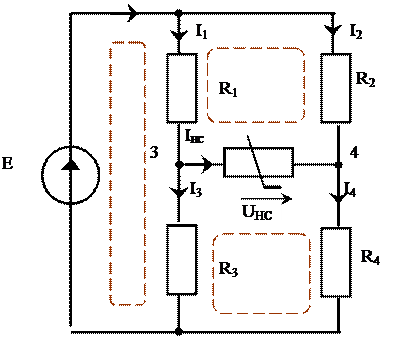
В цепи с нелинейным элементом НЭ рис. 7а. определить токи во всех ветвях.

Значения элементов цепи:   E = 20 B; ; R₁ = 10 Ом; R₂ = 40 Ом; R₃ = 40 Ом; R₄ = 10 Ом; вольт-амперная характеристика НЭ приведена на рис 7б

 

а                                                                                               б

Рис. 7

Решение

1. Линейную часть цепи (рис 7, а), относительно зажимов нелинейного элемента, представляем эквивалентным генератором рис. 2

 

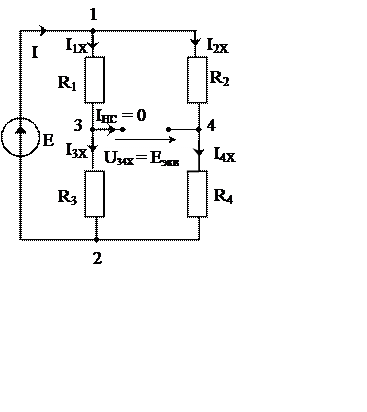а                                                                                               б

Рис. 8

1.1. Определим E_экв, для чего из схемы рис. 7а удалим нелинейное сопротивление HC и определим напряжение на разомкнутых зажимах 3-4 нелинейного сопротивления. Расчётная схема приведена на рис. 8б.

I_1X = I_3X = 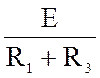 =  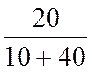= 0.4 A.

I_2X = I_4X = 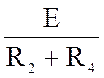 =  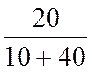= 0.4 A.

U_34X = E_экв = I_3X R₃ – I_4X R₄ = 0.4 (40 – 10) = 12 B.

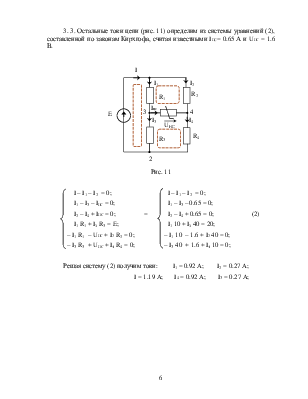
1.2. Определим R_экв, для чего источник ЭДС закоротим. Расчётная схема приведена на рис. 9.

 

Рис. 9

R_BX34 = R_экв = 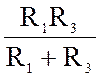 + 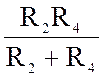=  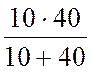+ 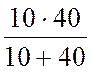= 16 Ом.

2. В одной системе координат строим линейную ВАХ эквивалентного генератора U₃₄(I)= E_ЭКВ - I·R_экв (U₃₄(I)= 12 - I·16) и ВАХ нелинейного элемента U_HC(I) (рис. 7б); в точке «а» (рис 10) пересечения построенных ВАХ,  определяются напряжение и ток в нелинейном сопротивлении U_НС и I_НС.

 

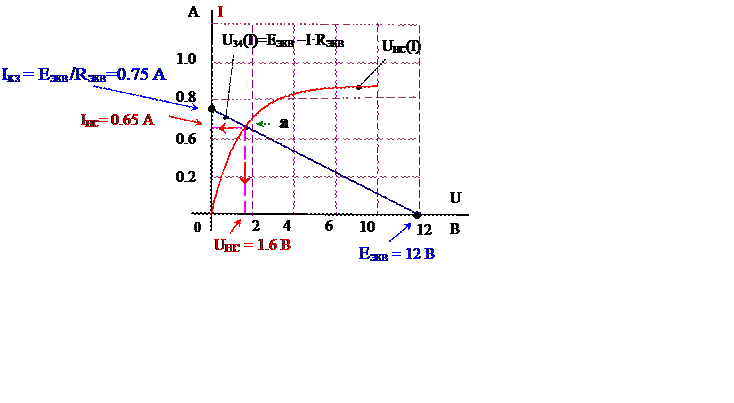Рис. 10

3. 3. Остальные токи цепи (рис. 11) определим из системы уравнений (2), составленной по законам Кирхгофа, считая известными I_НС= 0.65 А и U_HC = 1.6 В.

		I
				2

 

Рис. 11

I – I₁ – I₂  = 0;                                  I – I₁ – I₂  = 0;

I₁ – I₃ – I_HC = 0;                                I₁ – I₃ – 0.65 = 0;

I₂ – I₄ + I_HC = 0;                 =            I₂ – I₄ + 0.65 = 0;                                                            (2)

I₁ R₁ + I₃ R₃ = E;                              I₁ 10 + I₃ 40 = 20;

– I₁ R₁  – U_HC + I₂ R₂ = 0;                  – I₁ 10  – 1.6 + I₂ 40 = 0;

– I₃ R₃  + U_HC + I₄ R₄ = 0;                  – I₃ 40  + 1.6 + I₄ 10 = 0;

Решая систему (2) получим токи:        I₁ = 0.92 A;        I₂ = 0.27 A;

I = 1.19 A;       I₄ = 0.92 A;       I₃ = 0.27 A;