16.Метод квадратного корня
Этот
метод используется для решения систем линейных алгебраических уравнений с
эрмитовой невырожденной матрицей ![]() . Матрица
. Матрица ![]() называется эрмитовой, если она
совпадает со своей комплексно-сопряженной транспонированной матрицей, т.е.
называется эрмитовой, если она
совпадает со своей комплексно-сопряженной транспонированной матрицей, т.е. ![]() . Среди прямых методов этот метод
является самым быстродействующим и особенно удобен для решения систем уравнений
с ленточной матрицей, у которой
. Среди прямых методов этот метод
является самым быстродействующим и особенно удобен для решения систем уравнений
с ленточной матрицей, у которой ![]() при
при ![]() , где
, где ![]() .
Будем искать разложение действительной матрицы
.
Будем искать разложение действительной матрицы ![]() системы
(4.1) в виде
системы
(4.1) в виде ![]() ,(4.14) где ,
,(4.14) где ,
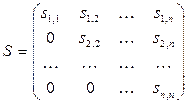
![]() - диагональная
матрица с элементами
- диагональная
матрица с элементами ![]() . После перемножения матриц
получаем
. После перемножения матриц
получаем
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Потребуем,
чтобы элементы ![]() были положительными
числами. Тогда получим
были положительными
числами. Тогда получим
(4.15)
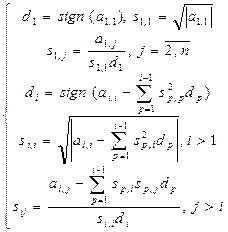 Таким образом, разложение (4.14)
существует и определяется формулами (2.15). Тогда решение системы (4.1)
сводится к решению двух систем с треугольными матрицами
Таким образом, разложение (4.14)
существует и определяется формулами (2.15). Тогда решение системы (4.1)
сводится к решению двух систем с треугольными матрицами ![]() ,
,
![]() .
.
Первая система имеет вид
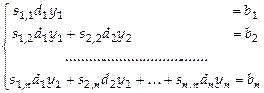
и
ее решение находится по формулам ![]() ,
, 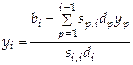 ,
, ![]() .
.
Вторая система
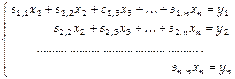 дает решение
исходной системы (4.1)
дает решение
исходной системы (4.1)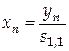 ,
, 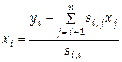 ,
,
![]() .
.
Если
матрица ![]() является положительно определенной
(все главные миноры положительны), то
является положительно определенной
(все главные миноры положительны), то ![]() и
и
![]() . Формулы разложения имеют в этом
случае вид
. Формулы разложения имеют в этом
случае вид
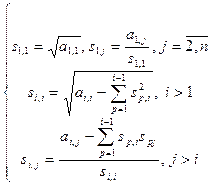
Для
решения системы линейных алгебраических уравнений с вещественной матрицей
порядка ![]() методом квадратного корня необходимо
выполнить
методом квадратного корня необходимо
выполнить ![]() операций умножения и деления и
операций умножения и деления и ![]() извлечений квадратного корня
извлечений квадратного корня
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.