Метод сопряженных градиентов для решения системы линейных алгебраических уравнений

18.Метод сопряженных градиентов

Метод сопряженных градиентов предназначен для решения систем линейных алгебраических уравнений с симметричной положительно определенной матрицей. Матрица  называется положительно определенной, если скалярное произведение  для всех ненулевых векторов x.Для того чтобы матрица  была положительно определенной необходимо и достаточно, чтобы все ее главные миноры были положительны. Рассмотрим систему линейных алгебраических уравнений (4.1) с положительно определенной симметричной матрицей. Пусть  - решение этой системы. Покажем, что в этом случае дает минимум функционала . Имеем

. Так как матрица  положительно определенная, то из последнего равенства следует, что решение  системы (4.1) дает минимум функционала . Будем искать этот минимум итерационным методом. Для этого предположим, что заданы два вектора  и . Последовательные приближения  к решению системы (4.1) будем строить по формулам, (4.22) , (4.23) где . (4.24) Параметры  и  будем определять из условия минимума функционала  в плоскости, проходящей через точку  и натянутой на векторы  и , т.е. минимум функционала ищется на множестве . Преобразуем наш функционал на этом множестве

 .

Для определения минимума  используем необходимое условие экстремума функции. Продифференцируем  по  и  и приравняем к нулю

,

.

Т.о., получаем систему уравнений ,(4.24). (4.25)

Так как  

, то последнюю систему можно представить в виде

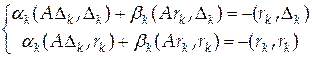 Это система двух уравнений с двумя неизвестными  и . Решая ее, получаем

,

Покажем, что метод сопряженных градиентов всегда сходится к решению системы . Учитывая (4.23)  -  (4.25) и ортогональность векторов  и , получим

   

.

Так как векторы  и  ортогональны, то из выражения для коэффициента  имеем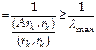, где  - наибольшее собственное значение матрицы . Окончательно получаем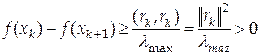. Таким образом, последовательность  монотонно убывает и ограничена снизу значением . Так как всякая монотонно убывающая последовательность сходится, т.е. , то по признаку Коши имеем . Тогда из последнего неравенства следует, что , а это означает, что последовательность векторов  сходится к решению  системы (4.1). Выберем начальные вектора  и  для метода сопряженных градиентов. Пусть  - произвольный вектор. Построим вектор , где вектор  выбирается по направлению  так, чтобы векторы  и  были ортогональными, т.е. . Обозначим . Тогда

.

Для выполнения условия ортогональности векторов  и  достаточно потребовать, чтобы

.Можно показать, что при таком выборе векторов  и итерации метода сопряженных градиентов обрываются не позднее, чем на -ом шаге, давая точное решение системы (4.1) ( - порядок системы). В сочетании с методом подавления компонент метод сопряженных градиентов позволяет находить решение за число итераций, значительно меньшее .Основной операцией метода сопряженных градиентов является вычисление произведений  и , причем ни в какие другие операции матрица  не входит. Поэтому максимальный порядок решаемых на ЭВМ систем уравнений зависит только от объема информации, необходимой для умножения матрицы  на вектор. Значит, применение метода сопряженных градиентов будет тем эффективнее, чем эффективнее составлена программа умножения матрицы на вектор.