Группа задач, порождаемая так называемой проблемой собственных значений

30-31.полная и частичная проблемы...

 Рассмотрим важную группу таких задач, порождаемую так называемой проблемой собственных значений. Собственным значением (или характеристиче­ским числом) квадратной матрицы А называется такое число λ, что для некоторого ненулевого вектора х имеет место равенство Ах= λ х. (5.0)Любой ненулевой вектор х, удовлетворяющий этому равенству, называ­ется собственным вектором матрицы А, соответствующим (или принадле­жащим) собственному значению λ. Очевидно, что все собственные век­торы матрицы определены с точностью до числового множителя. Анализ собственных значений матриц является важной темой научно-технических исследований.Условием существования у однородной системы   (5.0)  ненулевого решения (для наглядности запишем эту систему в виде  (А— λ Е)х = 0  является требование

|А- λ Е| = 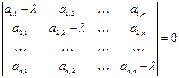Это уравнение обычно называют вековым (или характеристическим) уравнением матрицы А. Такие уравнения часто встречаются в приложе­ниях. Левая часть векового уравнения |А- λ Е|  = (-1)ⁿ (λⁿ – p₁ λ^n-1- p₂ λ^n-2 - …., -  р_п) носит название характеристического полинома матрицы А. Старший коэффициент этого полинома равен (—1)^п. Иногда вместо характеристи­ческого полинома рассматривают полином, отличающийся от характери­стического множителем (-1)^п. Этот полином Р( λ ) = λⁿ – p₁ λ^n-1- p₂ λ^n-2 - …., -  р_п  обычно называют собственным многочленом матрицы. Собственные зна­чения матрицы являются корнями собственного многочлена. Совокуп­ность всех собственных значений λ₁, λг, .... , λ_п матрицы А, где каждое собственное значение выписано столько раз, какова его кратность как корня  собственного  многочлена,   называется   спектром  этой   матрицы. Собственными же векторами матрицы А являются нетривиальные реше­ния однородной системы (5.0), в которой вместо λ подставлены соб­ственные значения λ_iматрицы. В том случае, когда для данного собствен­ного значения система (5.0)   имеет  несколько  линейно   независимых решений, этому собственному значению принадлежит несколько собст­венных векторов.  Задачу вычисления собственных значений и собственных векторов матрицы А можно разбить на три естественных этапа: 1) строение собственного многочлена  Р( λ ) матрицы; 2) решение уравнения Р(λ)=0  и  нахождение  собственных  значе­ний  λ_i (i=1, 2,... , п) матрицы; 3) отыскание нетривиальных решений однородных систем (А- λ_i Е)х = 0),(i=1,2.. ,n), т. е. нахождение собственных векторов матрицы. Каждый из трех отмеченных этапов решения проблемы собственных значений представляет собой достаточно сложную вычислительную задачу. В самом деле, построение собственного многочлена Р(λ), например, связано с развертыванием определителя

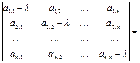(-1)ⁿ (λⁿ – p₁ λ^n-1- p₂ λ^n-2 - …., -  р_п) = (-1)ⁿ Р(λ),

что представляет собой значительные технические трудности. Основное затруднение вызвано тем обстоятельством, что λ входит в каждую строку и в каждый столбец определителя. В общем же случае, как известно из алгебры, коэффициенты p_iсобственного многочлена Р(λ) представляют собой взятые со знаком (-1)^i-1 суммы всех главных миноров (т. е. мино­ров, симметрично расположенных относительно главной диагонали) порядка iопределителя матрицы Л. Число таких миноров для каждого iравно числу сочетаний из п по i. Значит, непосредственное вычисление коэффициентов собственного многочлена Р(λ) квадратной матрицы по­рядка п связано с вычислением 2ⁿ -1 определителей различных порядков. Трудности в непосредственном осуществлении второго и третьего эта­пов решения проблемы собственных значений, т. е. трудности, связанные с решением алгебраических уравнений высоких степеней, и трудности в нахождении нетривиальных решений систем однородных линейных алгебраических уравнений, также значительны. К настоящему времени создано немало специальных вычислительных приемов, упрощающих численное нахождение собственных значений и собственных векторов матрицы. Все эти методы, как и в случае проблемы численного решения системы линейных алгебраических уравнений, мож­но разделить на точные и итерационные методы. К первой группе отно­сятся методы, по которым сначала строят собственный многочлен матри­цы (т. е. вычисляют его коэффициенты р_1, р₂, ... , р_п), затем, находя его корни, получают собственные значения матрицы и уже по ним находят соответствующие собственные векторы. Методы этой группы получили название точных методов в связи с тем обстоятельством, что в случае точного за­дания   (рациональными  числами)   элементов  матрицы   и  при   точном  (по правилам действий над обыкновенными дробями) проведении вычис­лений такие методы приводят к точным значениям коэффициентов соб­ственного многочлена, а координаты собственных векторов при этом оказываются выраженными через соответствующие собственные зна­чения. В методах второй группы собственные значения матрицы определя­ются непосредственно, без обращения к собственному многочлену, при этом обычно одновременно вычисляются и соответствующие собственные векторы. Вычислительные схемы таких методов носят итерационный характер. В них используется многократное умножение матрицы на вектор. Схемы этого типа обычно приводят к последовательности векто­ров, имеющей своим пределом собственный вектор, и к числовой после­довательности, предел которой является соответствующим собственным значением. Как правило, итерационные методы позволяют с достаточной точно­стью определить лишь первые (наибольшие по модулю, например) соб­ственные значения и соответствующие им собственные векторы. Поэтому методы этой группы чаще всего применяются к решению так называемой частичной проблемы собственных значений, т. е. их чаще используют лишь для отыскания одного или нескольких собственных значений матрицы и соответствующих собственных векторов. Точные же методы позволяют решать также и полную проблему собственных значений, т. е. дают возможность находить все собственные значения матрицы и все принадлежащие им собственные векторы. Полная проблема собственных значений в некоторых случаях может быть решена также и специаль­ными итерационными методами. Эти методы, конечно, более трудоемки, чем точные методы и чем итерационные методы решения частичной про­блемы собственных значений. Их практическое использование стало воз­можным лишь с появлением быстродействующих вычислительных машин. Однако перед точными методами решения полной проблемы собствейных значений итерационные методы имеют одно несомненное преимущество, связанное с возможностью нахождения всех собственных значений без предварительного построения собственного многочлена матрицы. Это особенно важно в связи с тем, что ошибки в вычислении коэффициентов собственного многочлена могут сильно сказываться на точности опре­деления его корней, т. е. на точности нахождения собственных значений исходной матрицы (и соответствующих им собственных векторов). Кроме того, большим достоинством итерационных методов перед точными является простота и единообразие производимых действий, что особенно цен­но при использовании быстродействующих вычислительных машин. Полная и частичная проблемы собственных значений сильно разли­чаются как по методам их решения, так и по области приложений. Так как решение полной проблемы собственных значений даже в случае матриц не очень высокого порядка обычно связано с очень большим объемом вычислительного труда, то возможность решения частичной проблемы собственных значений другими методами, минуя вычислитель­ные трудности решения полной проблемы, является очень ценной для практики. Таким образом, задача отыскания собственных значений и собственных векторов матрицы сводится к отысканию коэффициентов характеристического урав­нения, определению его корней, и к отысканию нетривиальных решений системы Ах = Х, в которой вместо Xрассматривают одно из найденных собственных значений. Наиболее простой метод определения собственных чисел и собственных векторов матрицы основан на методе непосредственного вычисления определителя.